Содержание
- 2. План урока Уравнения с параметрами 1 Решение уравнений 2 Неравенства с параметрами 3 Решение неравенств 4
- 3. Уравнения с параметрами В уравнениях иногда некоторые коэффициенты заданы не конкретными числами, а обозначены буквами. Такие
- 4. Решить уравнение с параметром – значит для любого допустимого значения параметра найти множество всех корней заданного
- 5. Линейное уравнение ax+b=с с неизвестным х можно рассматривать как уравнение с параметрами a, b, c. Его
- 6. Решение уравнений с параметрами Решить уравнение ax=3. Решение: Если Если а=0, то 0х=3 уравнение решений не
- 7. Решение уравнений с параметрами. 2. Решить уравнение: (a-2)x=a-2. 3. Решить уравнение: ax-6=x-1. 4.Решить уравнение : (a2-9)x=a+3.
- 8. Квадратные уравнения с параметрами. Решить уравнение ax=x2+3. Решение: Корней нет
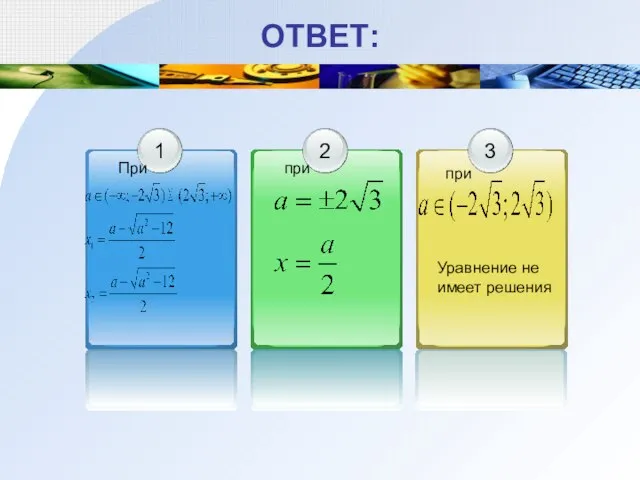
- 9. ОТВЕТ: Уравнение не имеет решения При при при
- 10. Квадратные уравнения с параметрами 2. Решите уравнение: a2x2+ax=0. 3.Решите уравнение: ax2+(2a2-1)x-2a=0. 4. Решите уравнение: (a+1)x2-2x+1-a=0. 5.
- 11. Домашнее задание: Решите уравнение: а) (a2-1)x=a+1; б) a2x=a(x+2)-2; в) (a2-1)x=a2+3x+2; г)ax2+2ax+4=0; д) (a-2)x2+2(a-2)x+2=0. 2. Для каждого
- 12. УРОК 2
- 13. Проверка домашнего задания 1 вариант 1.mx2+3mx-m-2=0 2.(a+1)x2-x+1-a=0 3. При каком положительном значении параметра с уравнение (2-c)x2-2(1+c)x+4=0
- 14. Решить уравнение 1. 2.
- 15. Неравенства с параметрами Решить неравенство с параметром – значит для любого допустимого значения параметра найти множество
- 16. Неравенства Решите неравенство: ax>3; 5x-a>ax-3; a(ax-4x)>a+2-4x; (x-a)(x-3) 0.
- 17. Самостоятельная работа РЕШИТЕ НЕРАВЕНСТВО: 2ax+5>a+10x; mx-6 2m-3x; (m-1)x
- 18. Решить линейное неравенство 1. 2. 3.
- 19. Домашнее задание Сколько решений имеет уравнение в зависимости от значений параметра Найдите значение параметра к, при
- 21. Скачать презентацию

















 и формирование отчетности
и формирование отчетности Презентация на тему Швейные товары
Презентация на тему Швейные товары  Филологи
Филологи АУДИТ
АУДИТ Проектирование СКС коттеджного участка из бруса
Проектирование СКС коттеджного участка из бруса Интеграция риск-менеджмента в ключевые процессы принятия решений
Интеграция риск-менеджмента в ключевые процессы принятия решений Проект: Юридическое сопровождение дополнительной эмиссии обыкновенных акций, размещаемых по открытой подписке
Проект: Юридическое сопровождение дополнительной эмиссии обыкновенных акций, размещаемых по открытой подписке Выполненное и планируемое благоустройство
Выполненное и планируемое благоустройство Вопросы составления и заверения отчетности получателей бюджетных средств в территориальных органах Федерального казначейства
Вопросы составления и заверения отчетности получателей бюджетных средств в территориальных органах Федерального казначейства Чудесные превращения воды в природе (3 класс)
Чудесные превращения воды в природе (3 класс) Волга – главный символ нашего края
Волга – главный символ нашего края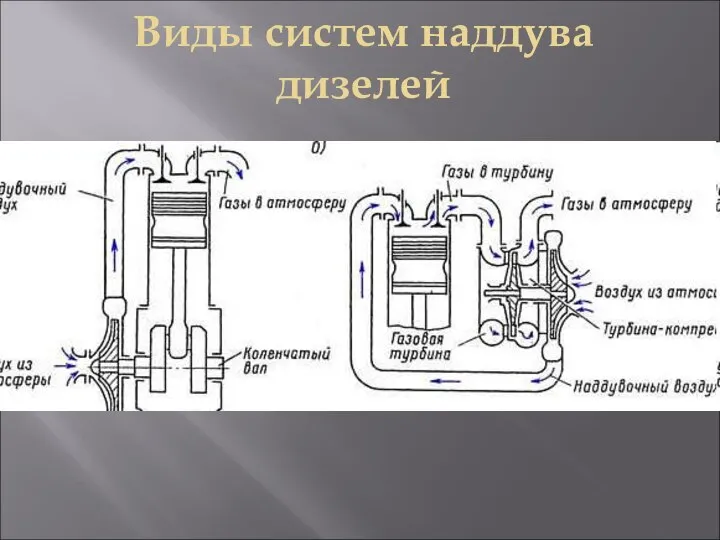 Виды систем наддува дизелей на судне. Аксиально-поршневой насос
Виды систем наддува дизелей на судне. Аксиально-поршневой насос Гражданское общество. Задания для выполнения
Гражданское общество. Задания для выполнения Природные и экологические опасности
Природные и экологические опасности London
London  Семейное право
Семейное право Morphonologie der Verben IPrasens
Morphonologie der Verben IPrasens Www.auditexpo.ru. Основные типы клиентов: Аналитический - ключевой вопрос: «Как?», «Зачем?» Рассудителен, Логичен, Собран, Нужны детали, Изуч
Www.auditexpo.ru. Основные типы клиентов: Аналитический - ключевой вопрос: «Как?», «Зачем?» Рассудителен, Логичен, Собран, Нужны детали, Изуч Мотивация продавцов-промоутеров SEB
Мотивация продавцов-промоутеров SEB Выражение характера человека в изображении. Женский образ русских сказок
Выражение характера человека в изображении. Женский образ русских сказок Портфолио
Портфолио Школьный музей "Родные истоки"
Школьный музей "Родные истоки" Тип, имя и значение переменной
Тип, имя и значение переменной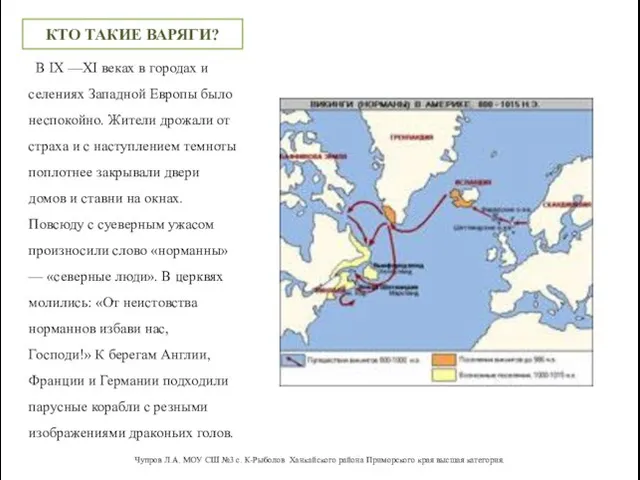 Путь из Варяг в Греки
Путь из Варяг в Греки Масштабируемое решениеот ЛПУ до региона
Масштабируемое решениеот ЛПУ до региона Агроэкосистеемы, или аграрные экологические системы
Агроэкосистеемы, или аграрные экологические системы Религия как одна из форм культуры
Религия как одна из форм культуры Угольная кислота
Угольная кислота