Закон Архимеда

Архимед (287 - 212 до н.э.)
Древнегреческий ученый, математики и изобретатель, родился в Сиракузах

Архимед ( 287 – 212 гг. до н.э.)
Архимед посвятил себя математике и механике. Сконструированные им аппараты и машины воспринимались современниками как чудеса техники. Он открыл закон об удельном весе и изучал теорию подъемных механизмов.
Среди его изобретений – Архимедов винт, устройство для поднятия воды или сыпучих материалов, таких как песок. Архимед говорил о рычаге, теорией которого он занимался: «Дайте мне точку опоры, и я переверну весь мир».

Закон Паскаля
Давление в жидкости или газе передается во всех направлениях одинаково и не зависит от ориентации площадки, на которую оно действует.

Давление жидкости на дно или боковые стенки сосуда зависит от высоты столба жидкости
Сила давления на дно цилиндрического сосуда высоты h и площади основания S равна весу столба жидкости mg,
где m = ρghS – масса жидкости в сосуде, ρ – плотность жидкости.

Давление столба жидкости ρgh называют гидростатическим давлением

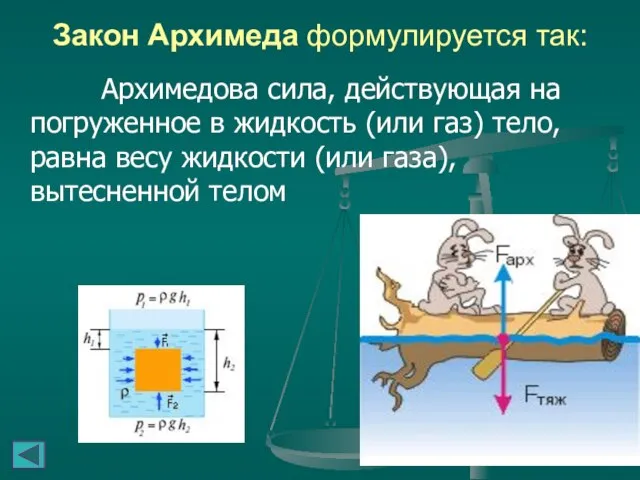
Закон Архимеда формулируется так:
Архимедова сила, действующая на погруженное в жидкость (или газ) тело, равна весу жидкости (или газа), вытесненной телом

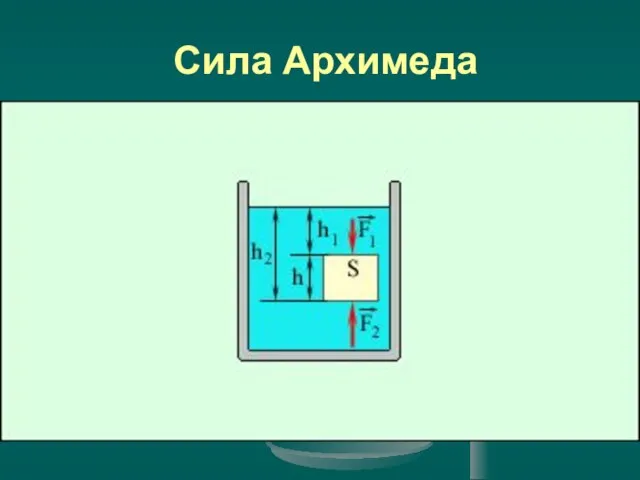
Сила Архимеда

В жидкость погружено тело в виде прямоугольного параллелепипеда высотой h и площадью основания S
Разность давлений на нижнюю и верхнюю грани есть:
Δp = p2 – p1 = ρgh.
Поэтому выталкивающая сила будет направлена вверх, и ее модуль равен
FA = F2 – F1 = SΔp = ρgSh = ρgV,
где V – объем вытесненной телом жидкости, а ρV – ее масса

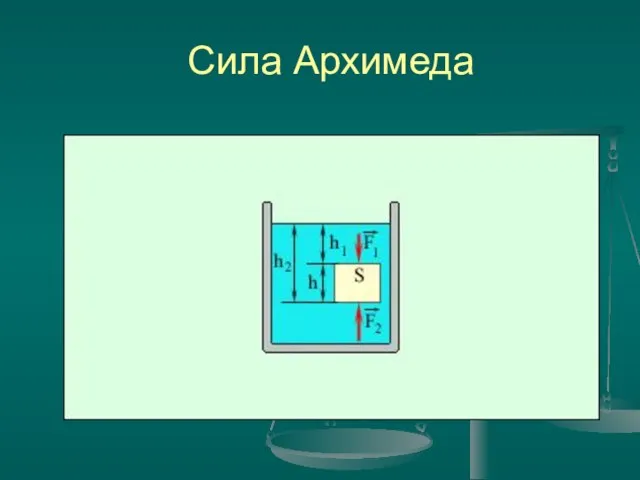
Сила Архимеда

Сила Архимеда
Причина возникновения выталкивающей силы в разности сил на разных глубинах

"Э-В-Р-И-К-А!"
На тело, погруженное в жидкость или газ, действует выталкивающая …………….
сила, …равная
…весу жидкости или газа, .
вытесненного
этим……. Телом!!!!!
FАрхимеда= Рж gV

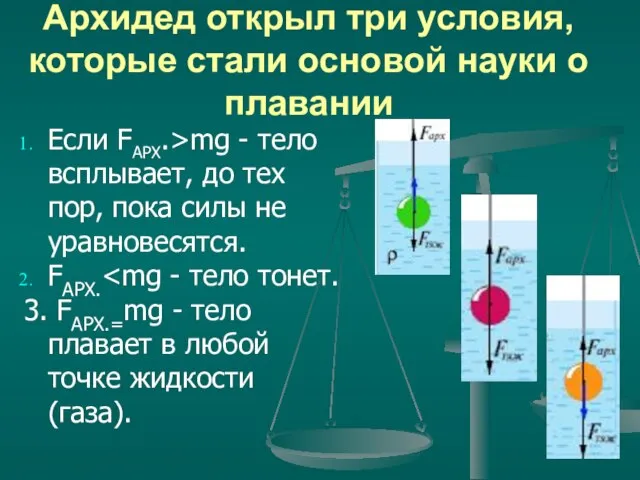
Архидед открыл три условия, которые стали основой науки о плавании
Если FАРХ.>mg - тело всплывает, до тех пор, пока силы не уравновесятся.
FАРХ.
3. FАРХ.=mg - тело плавает в любой точке жидкости (газа).

Сила Архимеда равна произведению плотности жидкости на коэффициент g и на объем тела

Условие плавания тел
Если плотность тела больше плотности жидкости, то тело в ней тонет.
Если плотность тела меньше плотности жидкости, то тело в ней всплывает.
При равенстве плотностей тела и жидкости, тело плавает.

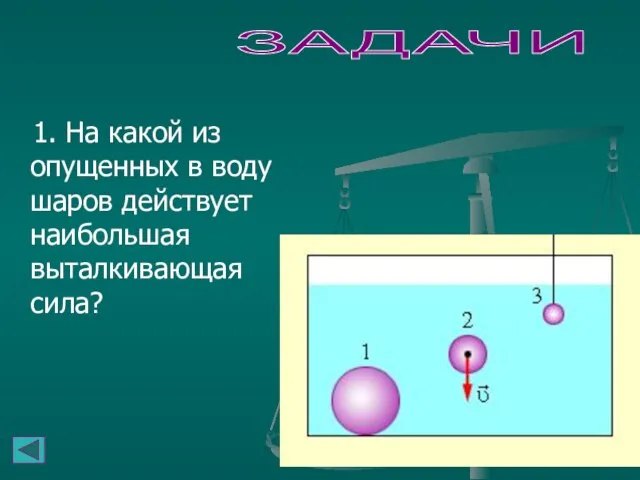
ЗАДАЧИ
1. На какой из опущенных в воду шаров действует наибольшая выталкивающая сила?

2. В сосуде с водой плавает брусок из льда, на котором лежит деревянный шар. Плотность вещества шара меньше плотности воды. Изменится ли уровень воды в сосуде, если лед растает?
ЗАДАЧИ

ЗАДАЧИ
3. В сосуде с водой плавает железный коробок, ко дну которого при помощи нити подвешен стальной шар. Шар не касается дна сосуда.
Как изменится высота уровня воды в сосуде, если нить, удерживающая шар, оборвется?

ЗАДАЧИ
Надводная часть айсберга имеет объем ΔV = 500 м3.
Найти объем айсберга V, если плотность льда ρльда = 0,92 г/см3, а плотность воды ρводы = 1,03 г/см3.

Решение:
Условие равновесия айсберга:
FАрхимеда = Mg
ρvg ∙ (V – ΔV) = ρльдаgV.
Откуда:

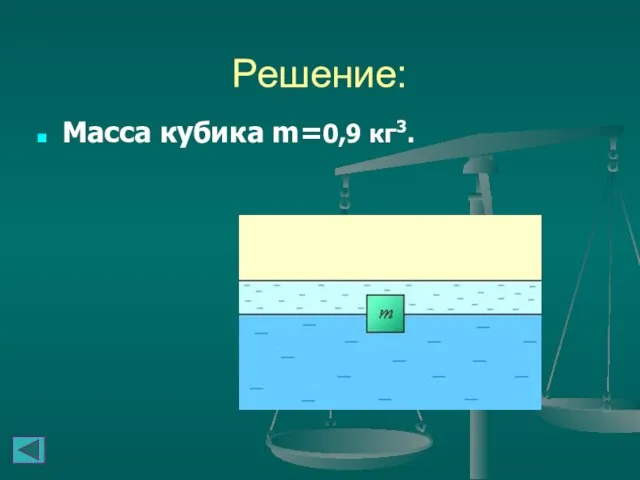
ЗАДАЧИ
Кубик с ребром 10 см погружен в сосуд с водой, на которую налита жидкость плотностью 0,8 г/см3, не смешивающаяся с водой. Линия раздела жидкостей проходит посередине высоты кубика.
Найти массу кубика.

Решение:
Масса кубика m=0,9 кг3.

ЗАДАЧИ
Определите объем вакуумной полости ΔV в куске железа массой m = 7,8 кг и плотностью ρж = 7800 кг/м3, если вес этого куска в воде Р = 60 Н. Плотность воды ρв = 1000 кг/м3. Ускорение свободного падения считать равным 10 м/с2.
Ответ выразить в
кубических см.

Решение:
Вес куска железа в воде равен:
P = mg – FA, где FA – сила Архимеда.
, где – объем железа в куске. Откуда

ЗАДАЧИ
Найдите плотность газа, заполняющего невесомую оболочку воздушного шара объемом 40 м3, если шар с грузом массой
m = 20 кг висит неподвижно.
Плотность воздуха ρв = 1,5 кг/м3.

Решение:
Условие равновесия шара:
mg + ρгазаgV = ρвоздухаgV.
Откуда:

ЗАДАЧИ
На какое минимальное давление должна быть рассчитана подводная лодка, глубина погружения которой H = 800 м? Ускорение свободного падения принять равным 10 м/с2, а одну атмосферу 100 кПа.Ответ выразить в мегапаскалях.

Решение:
Гидростатическое давление определяется формулой p = ρgH = 103∙10∙800 = 106 = 8 МПа.
Ответ: 8 МПа.

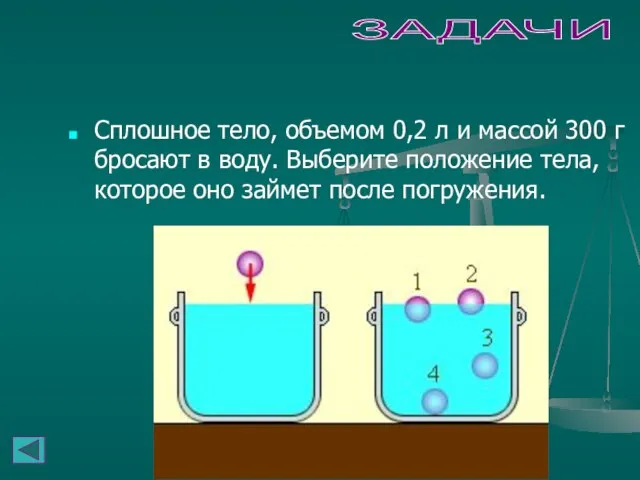
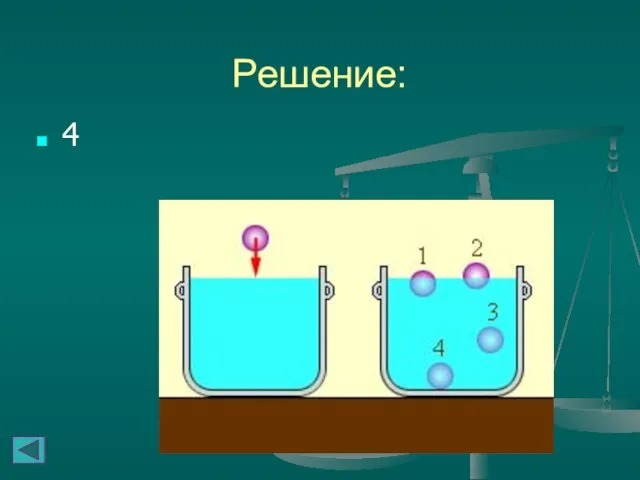
ЗАДАЧИ
Сплошное тело, объемом 0,2 л и массой 300 г бросают в воду. Выберите положение тела, которое оно займет после погружения.

Решение:
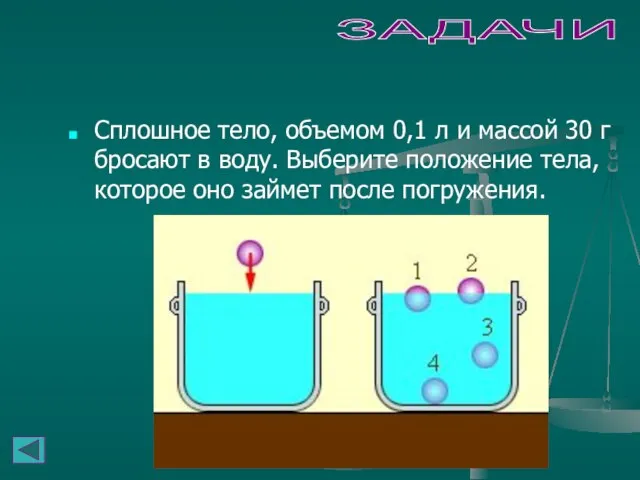
4

ЗАДАЧИ
Сплошное тело, объемом 0,1 л и массой 30 г бросают в воду. Выберите положение тела, которое оно займет после погружения.