Законы Кеплера – законы движения небесных тел

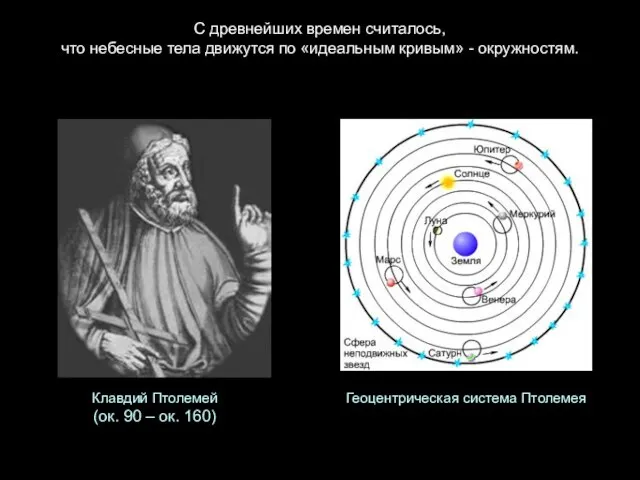
С древнейших времен считалось,
что небесные тела движутся по «идеальным кривым» - окружностям.
Геоцентрическая система Птолемея
Клавдий Птолемей
(ок. 90 – ок. 160)

В теории Николая Коперника, создателя гелиоцентрической системы мира,
круговое движение также не подвергалось сомнению.
Николай Коперник
(1473–1543)
Гелиоцентрическая система мира Коперника

Наблюдаемое положение планет
не соответствовало
предвычисленному в соответствии с теорией кругового движения планет вокруг Солнца.
Почему?
В XVII веке ответ на этот вопрос искал немецкий астроном Иоганн Кеплер.
Иоганн Кеплер
(1571–1630 )

Тихо Браге
(1546-1601)
Иоганн Кеплер изучал движение Марса по результатам многолетних наблюдений датского астронома Тихо Браге.

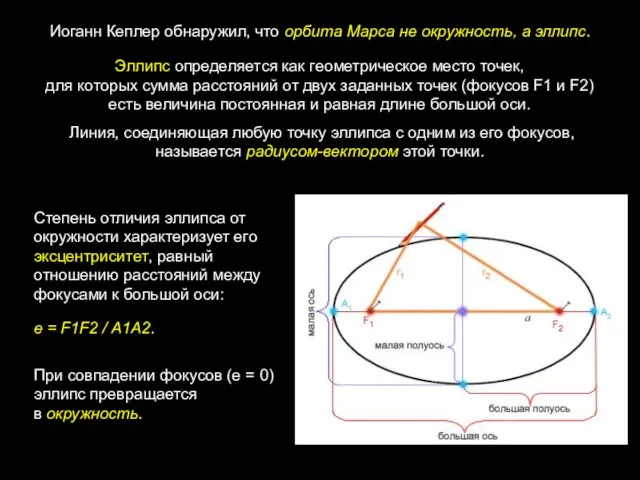
Эллипс определяется как геометрическое место точек, для которых сумма расстояний от двух заданных точек (фокусов F1 и F2)
есть величина постоянная и равная длине большой оси.
Линия, соединяющая любую точку эллипса с одним из его фокусов,
называется радиусом-вектором этой точки.
Иоганн Кеплер обнаружил, что орбита Марса не окружность, а эллипс.
Степень отличия эллипса от окружности характеризует его эксцентриситет, равный
отношению расстояний между фокусами к большой оси:
е = F1F2 / A1A2.
При совпадении фокусов (е = 0) эллипс превращается
в окружность.

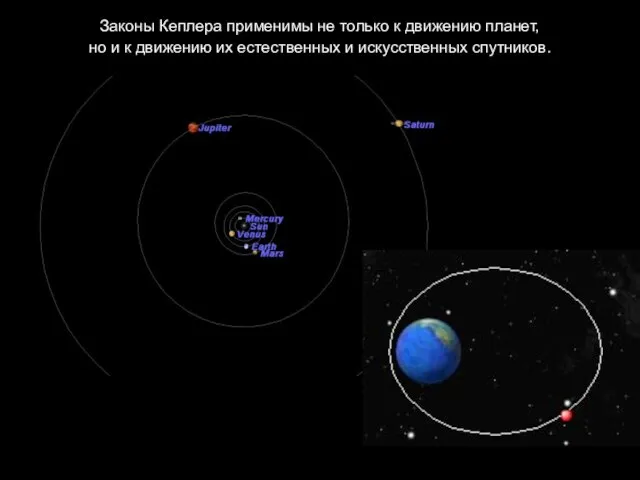
Законы Кеплера применимы не только к движению планет,
но и к движению их естественных и искусственных спутников.

Каждая планета движется по эллипсу,
в одном из фокусов которого находится Солнце.
Первый закон Кеплера:
Иллюстрация первого закона Кеплера
на примере движения спутников Земли

Орбиты планет – эллипсы, мало отличающиеся от окружностей,
так как их эксцентриситеты малы.

Большая полуось орбиты планеты – это ее среднее расстояние от Солнца.
Среднее расстояние Земли от Солнца принято в астрономии за единицу расстояния и называется астрономической единицей:
1 а.е. = 149 600 000 км.
Ближайшую к Солнцу точку орбиты называют перигелием (греч. пери – возле, около; Гелиос – Солнце), а наиболее удаленную – афелием (греч. апо – вдали).

По эллипсам движутся не только планеты,
но и их естественные и искусственные спутники.
Ближайшая к Земле точка орбиты Луны или искусственного спутника Земли называется перигеем (греч. Гея или Ге – Земля), а наиболее удаленная – апогеем.
Перигей
Апогей

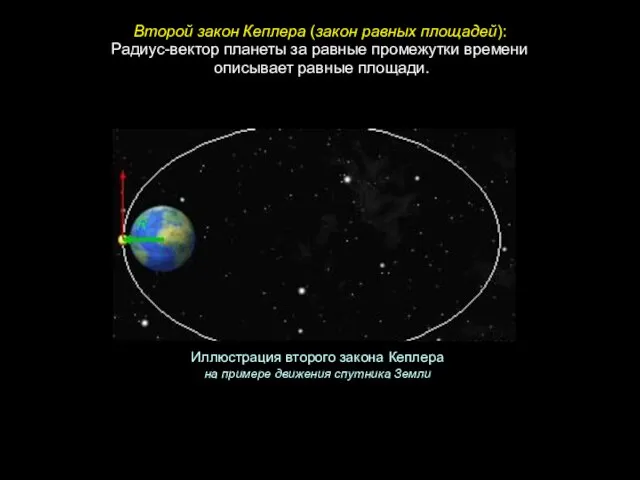
Радиус-вектор планеты за равные промежутки времени
описывает равные площади.
Второй закон Кеплера (закон равных площадей):
Иллюстрация второго закона Кеплера
на примере движения спутника Земли

Перигелий
Афелий
М1
М2
М3
М4
Планеты движутся вокруг Солнца неравномерно:
линейная скорость планет вблизи перигелия больше, чем вблизи афелия.
У Марса вблизи перигелия скорость равна 26,5 км/с, а около афелия - 22 км/с.
У некоторых комет орбиты настолько вытянуты, что вблизи Солнца их скорость доходит до 500 км/с, а в афелии снижается до 1 см/с.
S

Квадраты сидерических периодов обращений двух планет относятся
как кубы больших полуосей их орбит:
Третий закон Кеплера:
Иллюстрация третьего закона Кеплера
на примере движения спутников Земли

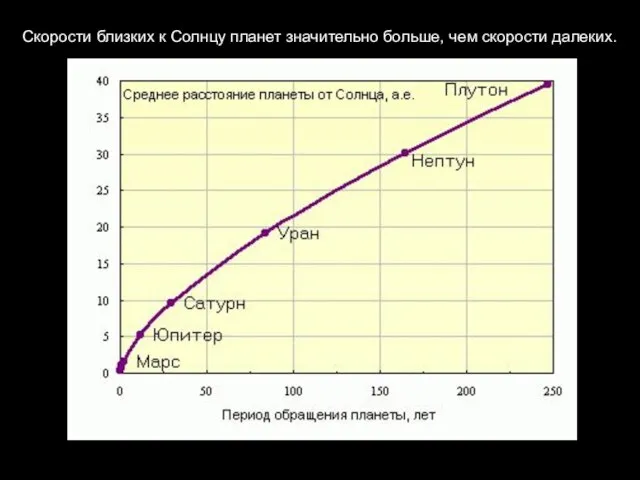
Скорости близких к Солнцу планет значительно больше, чем скорости далеких.

Квадраты сидерических периодов обращений двух планет относятся
как кубы больших полуосей их орбит.
Третий закон Кеплера
Каждая планета движется по эллипсу,
в одном из фокусов которого находится Солнце.
Первый закон Кеплера
Второй закон Кеплера
Радиус-вектор планеты за равные промежутки времени
описывает равные площади.
Кеплер исследовал движения всех известных в то время планет
и эмпирически вывел три закона движения планет относительно Солнца.

Какое расстояние называется астрономической единицей?
Среднее расстояние Земли от Солнца называется астрономической единицей.
Чему равна одна астрономическая единица?
1 а.е. = 149 600 000 км

Квадраты сидерических периодов обращений двух планет относятся
как кубы больших полуосей их орбит.
Третий закон Кеплера
Каждая планета движется по эллипсу,
в одном из фокусов которого находится Солнце.
Первый закон Кеплера
Второй закон Кеплера
Радиус-вектор планеты за равные промежутки времени
описывает равные площади.