Занимательная математика с играми, фокусами, задачами-шутками

Крупное научное открытие даёт решение крупной проблемы, но и в решении любой задачи присутствует крупица открытия.
Дьёрдь Пойа, венгерский математик

Игра «Не собьюсь»
Считать вслух до тридцати, но с одним условием – нельзя называть «три» (например, 13). Вместо этих чисел всегда нужно говорить «Не собьюсь!»

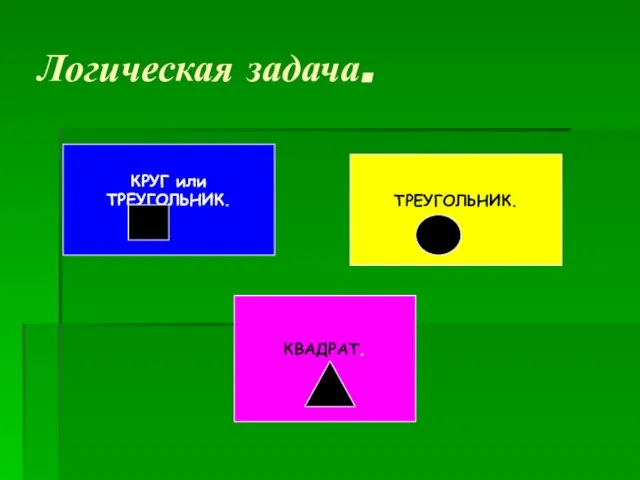
Логическая задача.
КВАДРАТ.
ТРЕУГОЛЬНИК.
КРУГ или ТРЕУГОЛЬНИК.

Уникурсальные фигуры.
Нарисовать фигуру одним росчерком

Задачи-шутки.
Если в 12ч ночи регулярно идет дождь, то можно ли ожидать, что через 168ч будет солнечная погода?
Летели утки – одна впереди и две позади, одна позади и две позади, одна между двумя и три в ряд. Сколько летело уток?
Как можно одним мешком пшеницы, смолов ее, наполнить 2 таких мешка?

Математические фокусы.
Задумай число.
Прибавь 4.
Умножь его на 3.
Прибавь 3.
Удвой результат.
Вычти 12.
Результат раздели на 6.
Вычти задуманное число.
Результат умножь на 4.

Обманутый хозяин
Хозяин устроил в своем погребе шкаф в форме квадрата с девятью отделениями. Среднее (внутри) отделение он оставил свободным для пустых бутылок, а в остальных расположил 60 бутылок вина так, что в каждой стороне по 21 бутылке,(рис. 1). Слуга заметил, что хозяин проверял число бутылок, считая только бутылки по сторонам квадрата, следя за тем, чтобы на каждой стороне квадрата былопо21 бутылке. Тогда слуга унес сначало 4 бутылки, а остальные расставил так, что вновь получил 21 бутылку н каждой стороне квадрата (рис 2). Так он повторял, пока было возможно. Сколько раз он драл бутылки и сколько бутылок унес?

А Б

Уникурсальные кривые
Уникурсальной кривой может быть любое число четных узлов, но не более двух нечетных;
Если в фигуре только четные узлы, то обход обход можно начать с лююбой точки
если в фигуре два нечетных узла, нужно начинать с одной из них,а заканчивать – в ддругом нечетном узле.