Жизнь фракталов

Цели и задачи

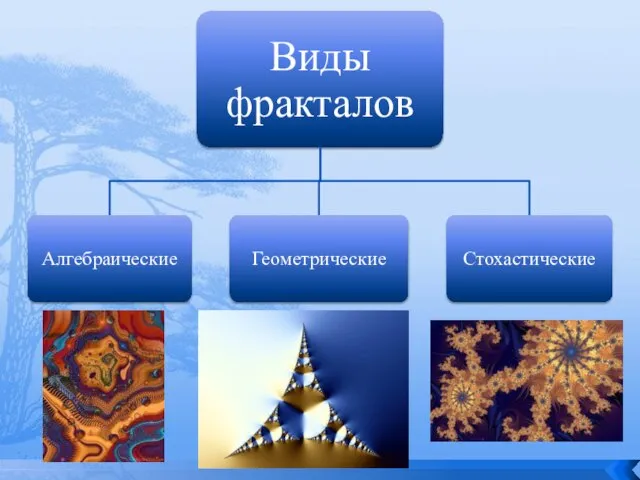
Содержание
Введение
Определение фрактала
История открытия
Виды фракталов
Значение и применение
Вывод

Фрактал
Фракта́л (лат. fractus — дроблёный, сломанный, разбитый) — сложная геометрическая фигура, обладающая свойством самоподобия, то есть составленная из нескольких частей, каждая из которых подобна всей фигуре целиком.
Фрактал — это бесконечно самоподобная геометрическая фигура, каждый фрагмент которой повторяется при уменьшении масштаба

Алгебраические фракталы
Вторая большая группа фракталов - алгебраические. Свое название они получили, за то, что их строят, используя простые алгебраические формулы. Получают их с помощью нелинейных процессов в n-мерных пространствах.
Самыми известными из них являются множества Мандельброта и Жюлиа, Бассейны Ньютона и т.д.

Геометрические фракталы
Именно с них и начиналась история фракталов. Этот тип фракталов получается путем простых геометрических построений. Геометрические фракталы являются самыми наглядными, т.к. геометрические фракталы обладают самоподобностью, не изменяющейся при изменении масштаба.
Треугольник Серпинского

Стохастические фракталы
Фракталы при построении которых случайным образом изменяются какие-либо параметры называются стохастичными. Термин "стохастичность" происходит от греческого слова, обозначающего "предположение".
Эти фракталы используются при моделировании рельефов местности и поверхности морей, процесса электролиза.

История открытия
Понятия фрактал было предложено Бенуа Мандельбротом в 1975 году для обозначения нерегулярных, но самоподобных структур, которыми он занимался. Рождение фрактальной геометрии принято связывать с выходом в 1977 году книги Мандельброта `The Fractal Geometry of Nature'. В его работах использованы научные результаты других ученых, работавших в период 1875-1925 годов в той же области (Пуанкаре, Фату, Жюлиа, Кантор, Хаусдорф). Но только в наше время удалось объединить их работы в единую систему
Формула Мандельброта, объединяющая все множества Жюлиа в одно изображение.
F(z) = f2 + c

Родоначальник фрактальной геометрии
Бенуа Мандельброт родился в Варшаве в 1924 году в семье литовских евреев. В 1936 году вся семья эмигрировала во Францию и поселилась в Париже.
В 1958 году Мандельброт поселился в США, где приступил к работе в научно-исследовательском центре IBM в Йорктауне, поскольку IBM в то время занималась интересными Бенуа Мандельброту областями математики.
Исследуя экономику, Мандельброт обнаружил, что произвольные внешне колебания цены могут следовать скрытому математическому порядку во времени, который не описывается стандартными кривыми.

Применение:
Радиотехника
Фрактальные антенны
Использование фрактальной геометрии при проектировании антенных устройств было впервые применено американским инженером Натаном Коэном. Натан вырезал из алюминиевой фольги фигуру в форме кривой Коха и наклеил её на лист бумаги, затем присоединил к приёмнику. Коэн основал собственную компанию и наладил их серийный выпуск.
Кривая коха

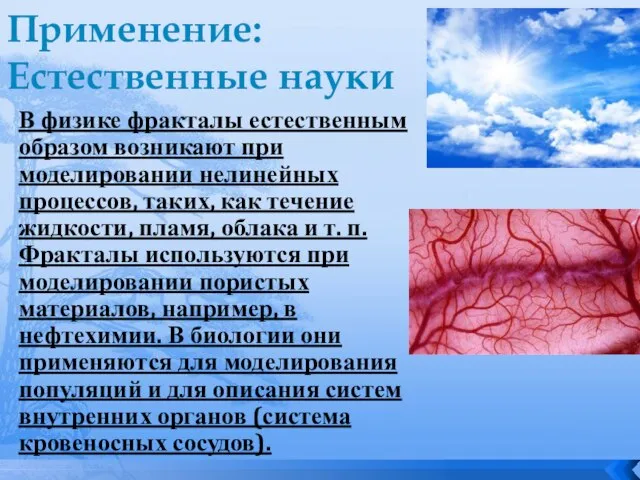
Применение:
Естественные науки
В физике фракталы естественным образом возникают при моделировании нелинейных процессов, таких, как течение жидкости, пламя, облака и т. п. Фракталы используются при моделировании пористых материалов, например, в нефтехимии. В биологии они применяются для моделирования популяций и для описания систем внутренних органов (система кровеносных сосудов).

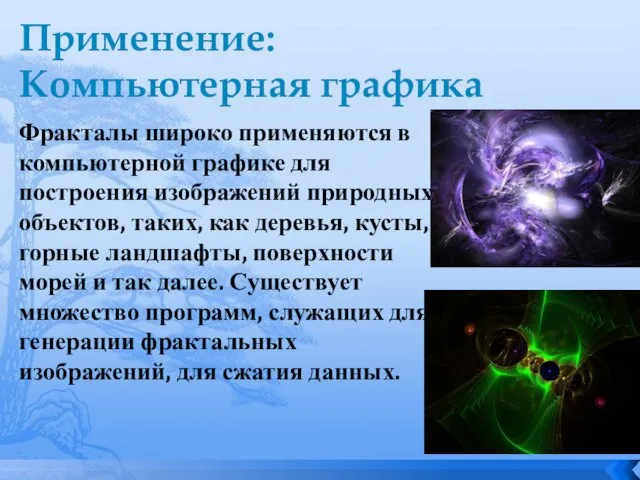
Применение:
Компьютерная графика
Фракталы широко применяются в компьютерной графике для построения изображений природных объектов, таких, как деревья, кусты, горные ландшафты, поверхности морей и так далее. Существует множество программ, служащих для генерации фрактальных изображений, для сжатия данных.

Применение:
Живопись
Некоторые художники, в том числе жившие до Б.Мандельброта, использовали (и сейчас используют) фракталы в своём творчестве. Одним из них был Кацусико Хокусай. Например, на его картине «Большая волна в Канагаве» гребни больших волн состоят из множества более мелких волн.

Применение:
Биология
Фракталы нашли широкое применение и в биологии. Учёные, изучая сосудистую систему выяснили, что её участки можно представить в виде фракталов. Далее, изучая различные участки, они выяснили, что здоровые кровеносные сети и раковые опухоли имеют разную фрактальную структуру. Это может помочь при выявлении раковых опухолей на ранней стадии.

Галерея:
Биология

Применение фракталов в дизайне

Заключение
В ходе выполнения данной работы я изучил найденные мной текстовые и мультимедиа материалы и узнал, что же представляют собой фракталы, на какие виды они делятся и где применяются. На основе изученного материала можно сделать вывод, что фракталы находят применение в различных сферах деятельности человека (информатика, живопись, радиотехника), а также в некоторых науках, а именно в физике, биологии, химии и, конечно, в математике. Но наиболее часто фракталы используются при описании природных объектов и некоторых процессов, а также при их моделировании.