Слайд 2История золотого сечения
Принято считать, что понятие о золотом делении ввел в научный

обиход Пифагор
Слайд 3Золотое сечение в математике
Ряд чисел 0,1,1,2,3,5,8,13,21,34,55 и т.д. известен как ряд Фибоначчи.

Особенность последовательности чисел состоит в том, что каждый её член, начиная с третьего, равен сумме двух предыдущих 2 + 3 = 5; 3 + 5 = 8; 5 + 8 =13; 8 + 13 =21; 13 + 21 = 34 и т.д., а отношение смежных чисел ряда приближается к отношению золотого деления. Так, 21 : 34 = 0,617, а 34 : 55 = 0,618. Это отношение обозначается символом Ф. Только это отношение - 0,618 : 0,382 – дает непрерывное деление отрезка прямой в золотой пропорции, увеличение его или уменьшение до бесконечности, когда меньший отрезок так относится к большему, как больший ко всему
Слайд 4Золотой прямоугольник
Золотой прямоугольник обладает многими интересными свойствами. Если, например, от золотого прямоугольника

АВСD отрезать квадрат со стороной, равной меньшей стороне прямоугольника, то снова получим золотой прямоугольник EFCD и т.д.
Слайд 5Золотое сечение в природе
Рассматривая расположение листьев на стебле растений можно заметить, что

между каждыми двумя парами листьев (А и С) третья расположена в месте золотого сечения (В).
Если первый отросток принять за 100 единиц, то второй равен 62 единицам, третий – 38, четвертый – 24 и т.д. Длина лепестков тоже подчинена золотой пропорции
Слайд 6Золотое сечение в теле человека
Золотое сечение заложено в пропорциях человеческого тела.
Примером является

статуя Зевса Олимпийского
(одно из семи чудес света)
Слайд 7Золотая пропорция в человеческом теле







 КОНКУРС по информационно-коммуникационным технологиям Проект: «Покрышкин А.И. –трижды Герой Советского Союза» Авт
КОНКУРС по информационно-коммуникационным технологиям Проект: «Покрышкин А.И. –трижды Герой Советского Союза» Авт And also in the retail business
And also in the retail business Порядок создания предприятия
Порядок создания предприятия Федорко Надежда Никифоровна
Федорко Надежда Никифоровна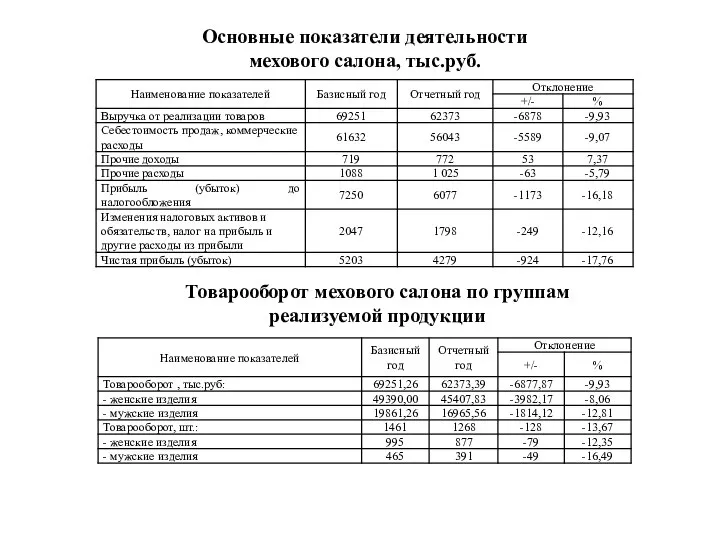 Товарооборот мехового салона по видам товарных групп
Товарооборот мехового салона по видам товарных групп ПРОВОДЯЩИЕ ПОЛИМЕРЫ
ПРОВОДЯЩИЕ ПОЛИМЕРЫ Дискуссия
Дискуссия Морская транспортная система
Морская транспортная система СПЕЦИАЛЬНОСТЬ«СТРАХОВОЕ ДЕЛО»
СПЕЦИАЛЬНОСТЬ«СТРАХОВОЕ ДЕЛО» Famous Psychologists Alfred Adler
Famous Psychologists Alfred Adler Аэромеханика
Аэромеханика Создание продукта
Создание продукта  The Incredible Sun
The Incredible Sun  Откуда взять клиентов? Эффективные инструменты привлечения и удержания клиентов в интернете Анна Банникова
Откуда взять клиентов? Эффективные инструменты привлечения и удержания клиентов в интернете Анна Банникова Класс Птицы 1 класс
Класс Птицы 1 класс Презентация на тему Различение частиц НЕ и НИ
Презентация на тему Различение частиц НЕ и НИ Ворлд Скилс. История
Ворлд Скилс. История «Вегетативное размножение махровой глоксинии листовыми черенками»
«Вегетативное размножение махровой глоксинии листовыми черенками» Феодальная раздробленность на Руси
Феодальная раздробленность на Руси Презентация на тему: Понятие квадратного корня из неотрицательного числа
Презентация на тему: Понятие квадратного корня из неотрицательного числа MY SPORT IDOL IS SVETLANA KHORKINA
MY SPORT IDOL IS SVETLANA KHORKINA  За 5 минут вендинговый автомат способен продать 25 единиц Товара. 5 минут – достаточно, чтобы проверить, какой Доход принес Ваш Биз
За 5 минут вендинговый автомат способен продать 25 единиц Товара. 5 минут – достаточно, чтобы проверить, какой Доход принес Ваш Биз Построение графика функции с помощью производной.
Построение графика функции с помощью производной. РЕАЛЬНІ ГАЗИ
РЕАЛЬНІ ГАЗИ  Презентация на тему Компьютерные сети Классификация
Презентация на тему Компьютерные сети Классификация  Сжатие данных
Сжатие данных Расшифровка сокращений в детализации и Мобильной детализации
Расшифровка сокращений в детализации и Мобильной детализации Что такое Андертейл
Что такое Андертейл