Содержание
- 2. Вероятность - одно из основных понятий теории вероятностей. Существует несколько определений этого понятия. Приведем определение, которое
- 3. Определение: Два события А и В называются независимыми, если появление одного из них не изменяет вероятности
- 4. Вероятность суммы двух событий. Теорема1: Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий: Р(А+В)=Р(А)+Р(В).
- 5. В случайном эксперименте бросают две игральные кости. Найдите вероятность того, что в сумме выпадет 8 очков.
- 6. В случайном эксперименте бросают три игральные кости. Найдите вероятность того, что в сумме выпадет 4 очка.
- 7. В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что орел выпадет ровно один раз.
- 8. В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что орел не выпадет ни разу.
- 9. В случайном эксперименте симметричную монету бросают трижды. Найдите вероятность того, что орел не выпадет ни разу.
- 10. В чемпионате по гимнастике участвуют 20 спортсменок: 8 из России, 7 из США, остальные − из
- 11. В среднем из 2000 садовых насосов, поступивших в продажу, 20 подтекают. Найдите вероятность того, что один
- 12. Решение: 120 + 9 = 129 – сумок всего (качественных и со скрытыми дефектами). Вероятность того,
- 13. В соревнованиях по толканию ядра участвуют 4 спортсмена из Финляндии, 7 спортсменов из Дании, 9 спортсменов
- 14. Научная конференция проводится в 5 дней. Всего запланировано 75 докладов − первые три дня по 17
- 15. Конкурс исполнителей проводится в 3 дня. Всего заявлено 40 выступлений − по одному от каждой страны.
- 16. На семинар приехали 3 ученых из Норвегии, 3 из России и 4 из Испании. Порядок докладов
- 17. Перед началом первого тура чемпионата по бадминтону участников разбивают на игровые пары случайным образом с помощью
- 18. В сборнике билетов по химии всего 35 билетов, в 7 из них встречается вопрос по кислотам.
- 19. На чемпионате по прыжкам в воду выступают 25 спортсменов, среди них 8 прыгунов из России и
- 21. Скачать презентацию


















 Чужая семья
Чужая семья Фоторассказ Гостеприимная волчица
Фоторассказ Гостеприимная волчица Молодежная инициатива«Выставка»
Молодежная инициатива«Выставка» Презентация на тему что у нас над головой презентация 1 класс
Презентация на тему что у нас над головой презентация 1 класс Эффективность деятельности бюрократических организаций (модель В. Нисканена)
Эффективность деятельности бюрократических организаций (модель В. Нисканена) Системно-деятельностный подход
Системно-деятельностный подход Диагностика и лечение симптоматических гипертоний
Диагностика и лечение симптоматических гипертоний  Гелий
Гелий Откуда взять клиентов? эффективные решения для интернет-магазинов Першко Мария Пермь, 15 марта 2012.
Откуда взять клиентов? эффективные решения для интернет-магазинов Першко Мария Пермь, 15 марта 2012. Тренд. Основные этапы исследования
Тренд. Основные этапы исследования Международный день театра кукол
Международный день театра кукол Минеральные вещества в пищевых продуктах
Минеральные вещества в пищевых продуктах УСТРОЙСТВО ОРИЕНТАЦИИ БУТЫЛОК (УНИВЕРСАЛЬНОЕ)
УСТРОЙСТВО ОРИЕНТАЦИИ БУТЫЛОК (УНИВЕРСАЛЬНОЕ) Стандарты второго поколения
Стандарты второго поколения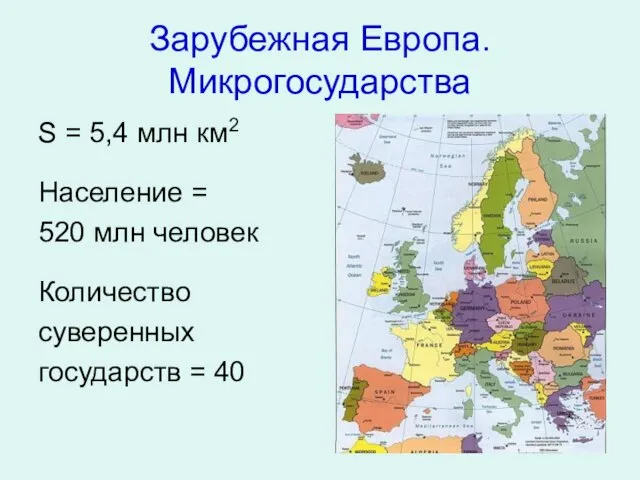 Зарубежная Европа. Микрогосударства
Зарубежная Европа. Микрогосударства Студентческое научное сообщество
Студентческое научное сообщество Обращение как живой свидетель истории
Обращение как живой свидетель истории Закономерности управления персоналом
Закономерности управления персоналом Презентация 2
Презентация 2 Политический режим. Демократия
Политический режим. Демократия Восток страны в федеральной региональной политике
Восток страны в федеральной региональной политике Старинный народный праздник Ярилин день (Макушка лета)
Старинный народный праздник Ярилин день (Макушка лета) Анализ тенденций развития химии на примере анализа Нобелевских премий по химии
Анализ тенденций развития химии на примере анализа Нобелевских премий по химии Заболевания, связанные с действием канцерогенов
Заболевания, связанные с действием канцерогенов Ладожское озеро
Ладожское озеро Пилотный проект Прямые выплаты в Волгоградской области с 1 июля 2020 года
Пилотный проект Прямые выплаты в Волгоградской области с 1 июля 2020 года WRITING AN INFORMAL LETTER
WRITING AN INFORMAL LETTER Индивидуальный итоговый проект: от замысла до защиты
Индивидуальный итоговый проект: от замысла до защиты