Слайд 2Возможности дисперсионного анализа:
1. Оценка силы и достоверности влияний.
2. Оценка разности частных средних и

частных долей.
3. Оценка наследуемости признаков в определенных группах особей при передаче генетической информации из поколения в поколение.
4. Анализ комбинационной способности ♀ и ♂ линий.
Слайд 3 Результативный признак – признак, изменяющийся под влиянием различных причин X, Y, Z.
Факторы,

вызывающие изменение признака, обозначаются А, В, С.
Организованные (регулируемые) факторы – испытывают серийно, в виде нескольких независимых друг от друга доз (градаций).
Слайд 4Типы дисперсионных комплексов:
• Однофакторные;
• Двух-, трех- и многофакторные;
• Равномерные, пропорциональные – ортогональные;
• Неравномерные – неортогональные.

Слайд 5Dy=Dx+De,
где Dx – межгрупповая дисперсия, представляющая собой сумму квадратов отклонений групповых

средних от общей средней комплекса, взвешенную на численность вариант в группах n.
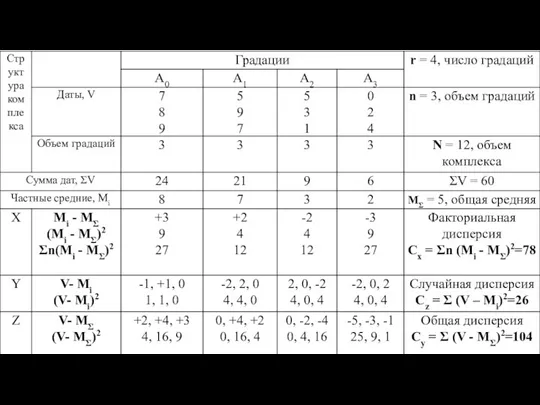
Слайд 61. Факториальная (межгрупповая) дисперсия равна сумме взвешенных квадратов центральных отклонений частных средних Мi

по градациям комплекса от общей средней МΣ:
Сх = Σn (Mi - MΣ)2
Слайд 7Случайная дисперсия (внутригрупповая) равна сумме квадратов центральных отклонений дат (V) от своих

частных средних (Mi) по градациям комплекса:
Сz = Σ (V – Mi)2
Слайд 8Общая дисперсия равна сумме квадратов центральных отклонений дат (V) от общей средней:
Сy

= Σ (V - MΣ)2
Слайд 10Закон аддитивности:
в любом дисперсионном комплексе сумма частных дисперсий (факториальной и случайной)

равна общей:
Сх+ Сz= Сy
(78+26)=104
Слайд 11Основной показатель силы влияния

Слайд 12Эмпирический критерий достоверности силы влияния

Слайд 14Фактически полученное дисперсионное отношение является величиной случайной, его необходимо сравнить с табличным

(стандартным) значением критерия Фишера Fst для принятого уровня значимости а и чисел степеней свободы. При этом число
степеней свободы для большей дисперсии находят в верхней
строке, а для меньшей - в первом столбце таблицы Фишера.












 Условия, необходимые для жизни организмов
Условия, необходимые для жизни организмов Болезни растений. Паразиты и болезни растений
Болезни растений. Паразиты и болезни растений Эндокриндік бездер. Гармондар
Эндокриндік бездер. Гармондар Выявление доминирующего полушария у учеников старшей школы гимназии №2
Выявление доминирующего полушария у учеников старшей школы гимназии №2 Бактерии - возбудители заболеваний человека
Бактерии - возбудители заболеваний человека Физиология микробов
Физиология микробов Презентация на тему Разнообразие грибов
Презентация на тему Разнообразие грибов  Отдел Моховидные. Класс Листостебельные (3)
Отдел Моховидные. Класс Листостебельные (3)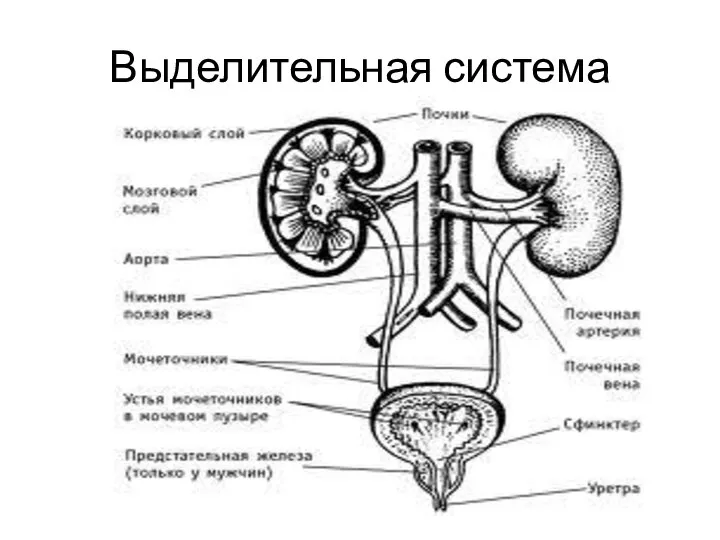 Выделительная система
Выделительная система Лестница жизни. Виды нуклениновых кислот. Д Н К
Лестница жизни. Виды нуклениновых кислот. Д Н К Ткани. Биология 8 класс
Ткани. Биология 8 класс Витамины и их роль в жизни человека
Витамины и их роль в жизни человека Корневое питание растений Учитель биологии МБОУ «СОШ» пст. Студенец Шосталь Е. А.
Корневое питание растений Учитель биологии МБОУ «СОШ» пст. Студенец Шосталь Е. А. Ребусы о растениях
Ребусы о растениях Спинной мозг
Спинной мозг Переваривание и всасывание белков. Продукты белкового обмена
Переваривание и всасывание белков. Продукты белкового обмена Строение и функции толстого кишечника
Строение и функции толстого кишечника Тип Споровики
Тип Споровики Лес - лёгкие планеты
Лес - лёгкие планеты Способы размножения ( 6 класс)
Способы размножения ( 6 класс) Презентация на тему Ткани растений
Презентация на тему Ткани растений  Презентация на тему ПРЕЗЕНТАЦИЯ ЗООЛОГИЯ – НАУКА О ЖИВОТНЫХ
Презентация на тему ПРЕЗЕНТАЦИЯ ЗООЛОГИЯ – НАУКА О ЖИВОТНЫХ  Анатомо-физиологические особенности человека в подростковом возрасте
Анатомо-физиологические особенности человека в подростковом возрасте Осенние цветы
Осенние цветы The perception of color
The perception of color Sapagyň meýilnamasy. Biologik baýlyklar barada düşünje
Sapagyň meýilnamasy. Biologik baýlyklar barada düşünje История одомашнивания перепелов
История одомашнивания перепелов Презентация на тему Биологические ритмы
Презентация на тему Биологические ритмы