Содержание
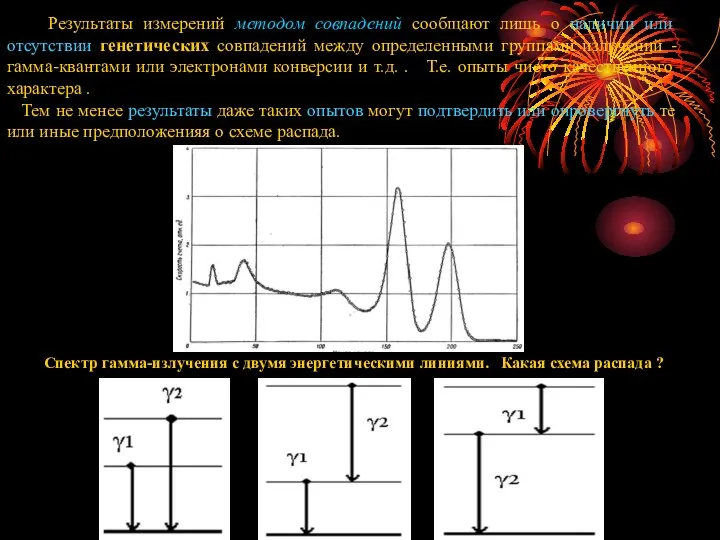
- 2. Результаты измерений методом совпадений сообщают лишь о наличии или отсутствии генетических совпадений между определенными группами излучений
- 3. Метод задержанных совпадений занимает значительное место в изучении времени жизни возбужденных состояний ядер. С его помощью
- 4. Спектрометрия задержанных совпадений С помощью двух детекторов регистрируют , например, γ-кванты. Регистрация сигналов определяет моменты образования
- 5. Спектрометр задержанных совпадений Блок-схема спектрометра задержанных совпадений В спектрометре используется разделение данных амплитудной и временной информации
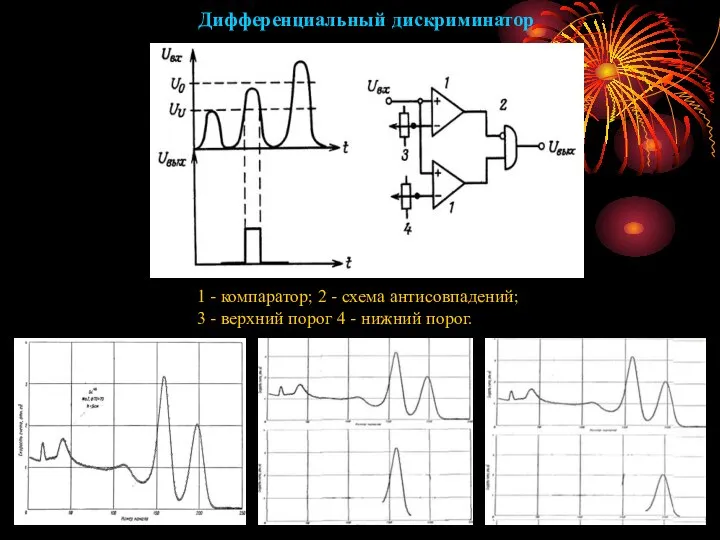
- 6. 1 - компаратор; 2 - схема антисовпадений; 3 - верхний порог 4 - нижний порог. Дифференциальный
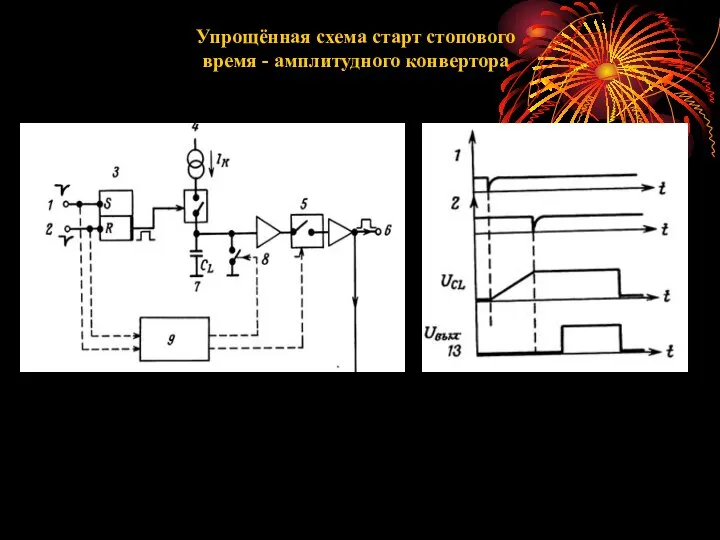
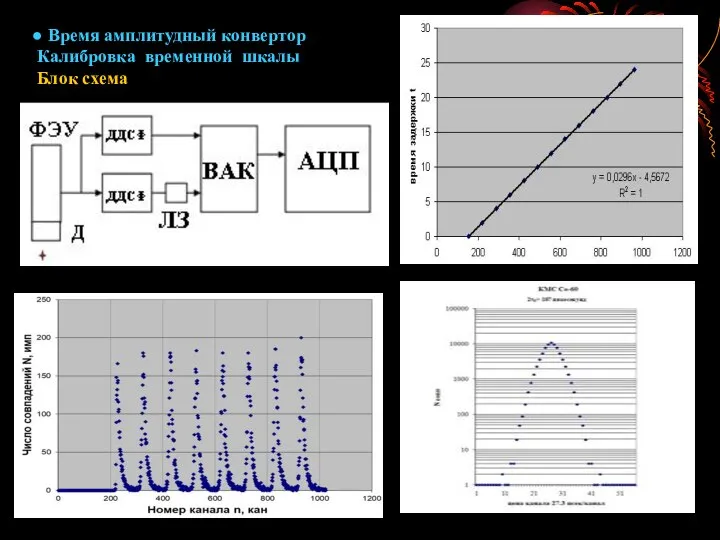
- 7. Упрощённая схема старт стопового время - амплитудного конвертора
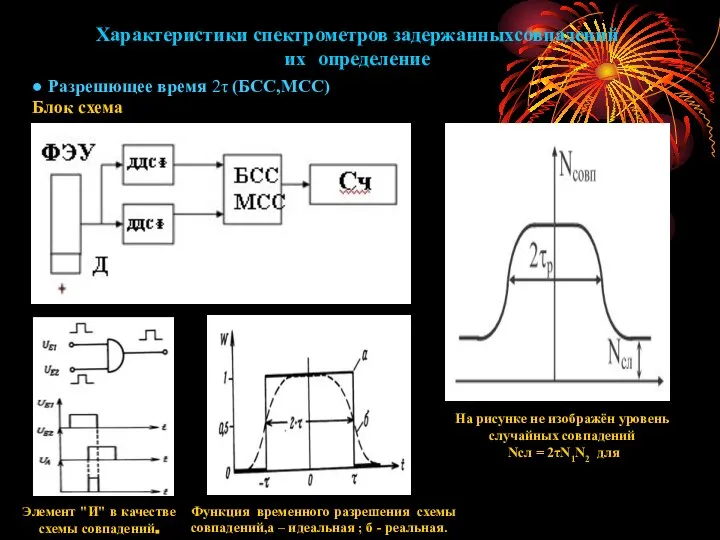
- 8. Характеристики спектрометров задержанныхсовпадений их определение ● Разрешющее время 2τ (БСС,МСС) Блок схема ФЭУ Элемент "И" в
- 9. ● Время амплитудный конвертор Калибровка временной шкалы Блок схема
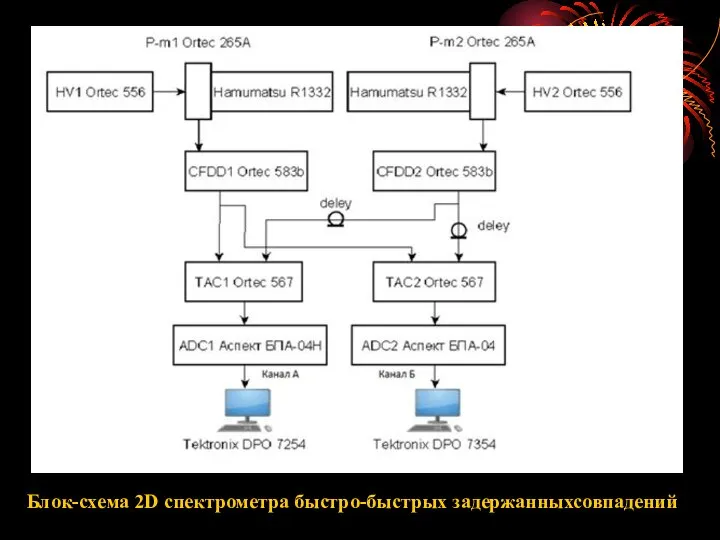
- 10. Блок-схема 2D спектрометра быстро-быстрых задержанныхсовпадений
- 11. Лекция 7 ( часть II ) Метод задержанных совпадений. Спектрометр задержанных совпадений Методы и устройства регистрации
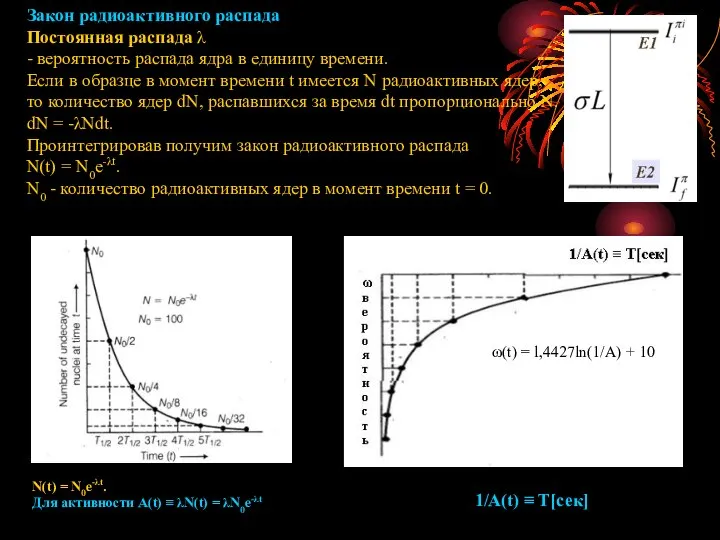
- 12. Закон радиоактивного распада Постоянная распада λ - вероятность распада ядра в единицу времени. Если в образце
- 13. Время жизни Tэксп возбужденного состоянии ядра определяется многими физическими факторами, связанными со структурой ядра, а также
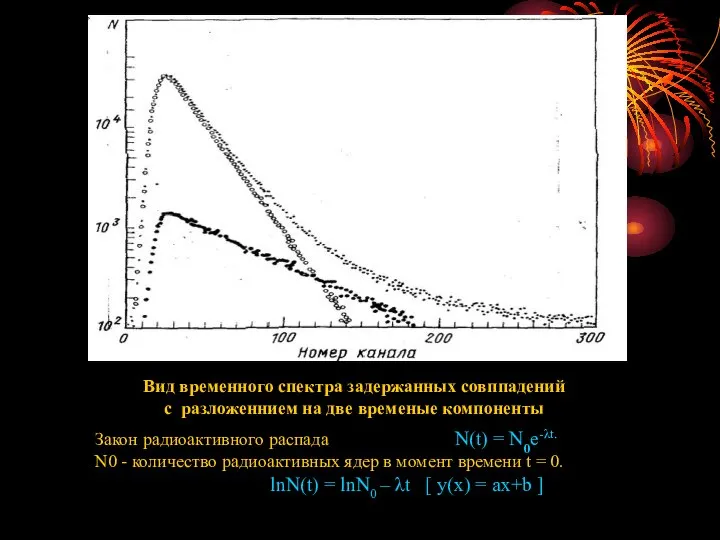
- 15. Вид временного спектра задержанных совппадений с разложеннием на две временые компоненты Закон радиоактивного распада N(t) =
- 16. Для простейшего случая одной компоненты и в предположении, что заселяющее излучение регистрируется одним каналом, а разряжающее
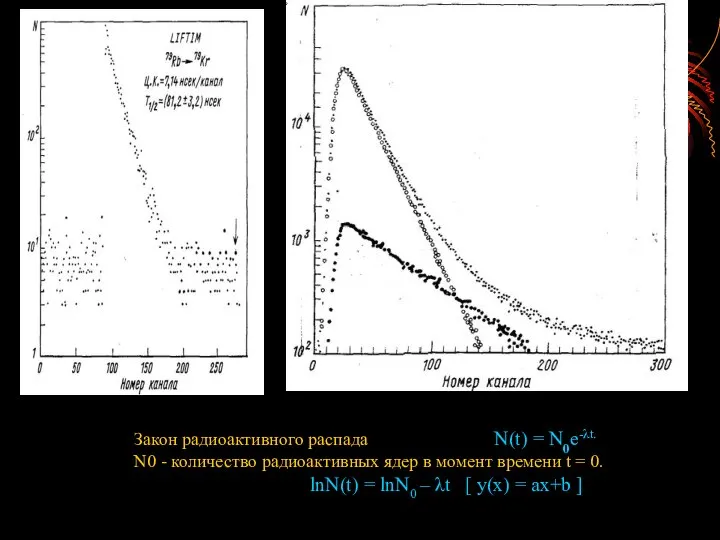
- 17. Закон радиоактивного распада N(t) = N0e-λt. N0 - количество радиоактивных ядер в момент времени t =
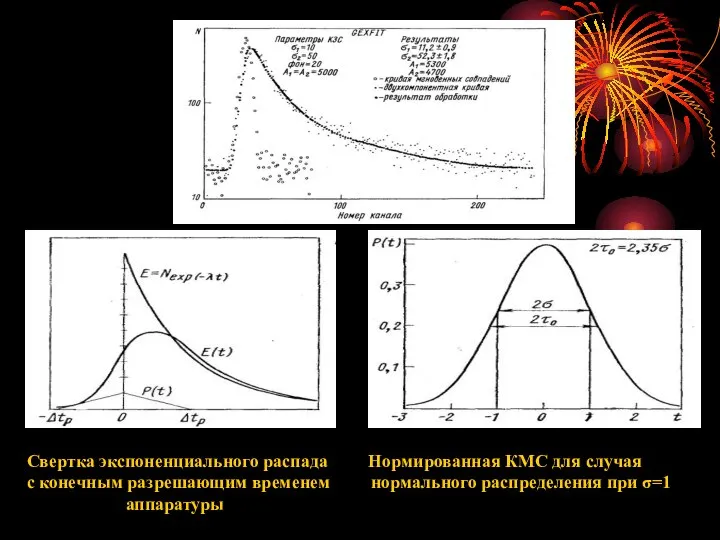
- 18. Свертка экспоненциального распада Нормированная КМС для случая с конечным разрешающим временем нормального распределения при σ=1 аппаратуры
- 19. Под кривой мгновенных совпадений (КМС) подразумевается экспериментальное временное распределение, измеренное для состояния, время жизни которого значительно
- 20. Метод наклона. Уравнение приводит к следующим dF(t)/dt = -λ[F(t)-P(t)] d/dt[lnF(t)] = -λ[1- P(t)/F(t)] Эти соотношения определяют
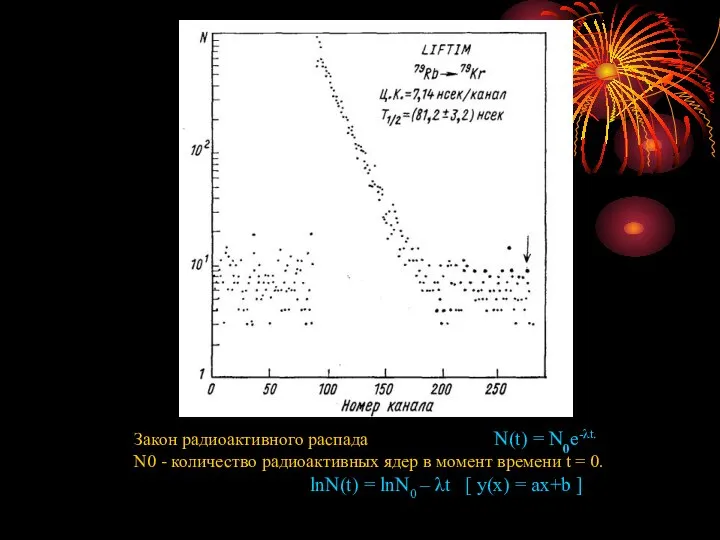
- 21. Закон радиоактивного распада N(t) = N0e-λt. N0 - количество радиоактивных ядер в момент времени t =
- 22. При обработке экспериментальных данных, в области, где F(t) >> P(t), по методу наименьших квадратов число совпадений
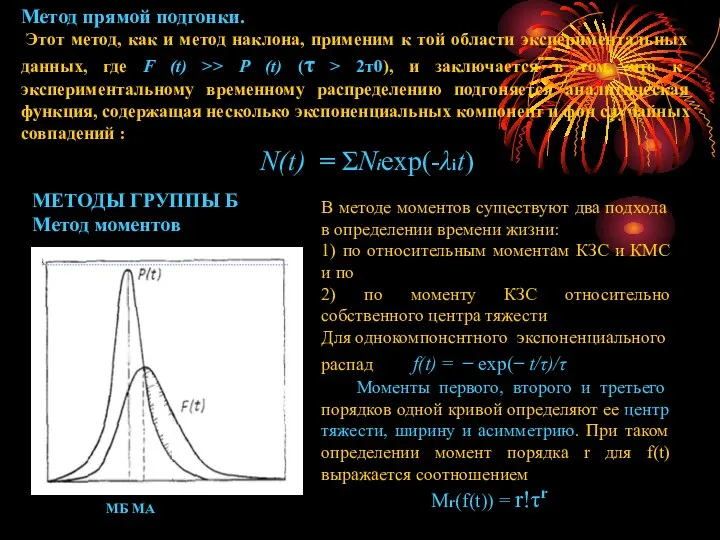
- 23. Метод прямой подгонки. Этот метод, как и метод наклона, применим к той области экспериментальных данных, где
- 24. Метод моментов приводит к следующим соотношениям между временами жизни τ и моментами K3С и КМС :
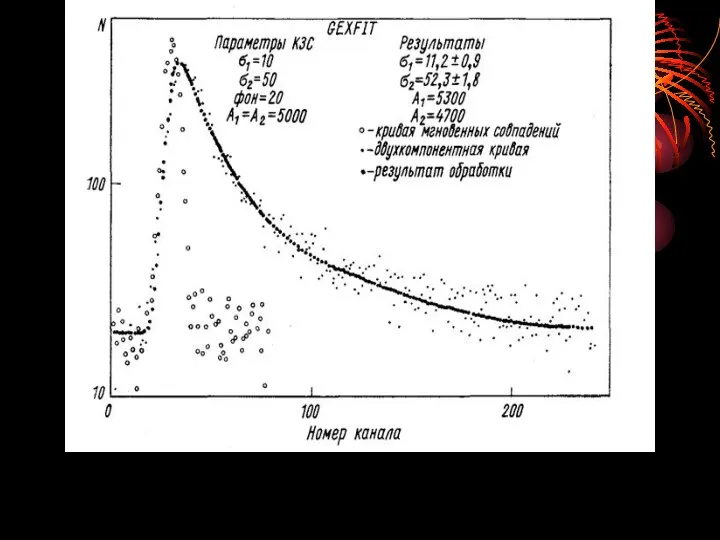
- 25. Методы свертки Ранее было показано, что вид КЗС является результатом свертки экспоненциального распределения с конечным временным
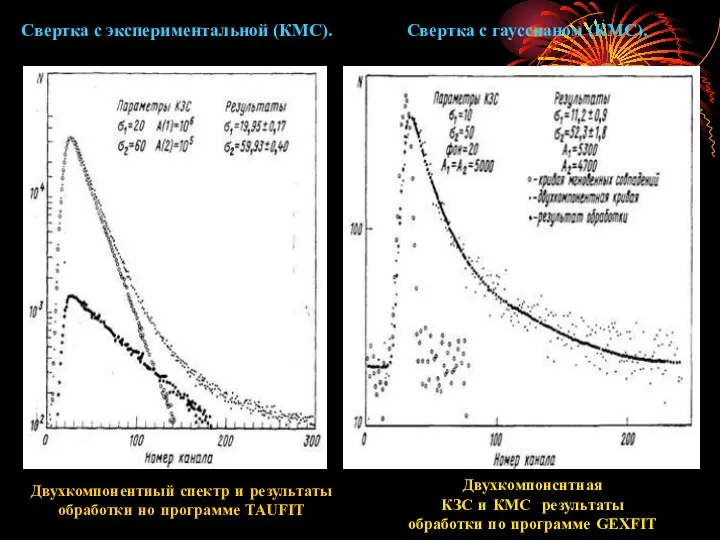
- 26. Свертка с гауссианом (КМС). Свертка с экспериментальной (КМС). Двухкомпонснтная КЗС и КМС результаты обработки по программе
- 27. Лекция 7 (часть II) Метод задержанных совпадений. Методы и устройства регистрации ионизирующих излучений
- 28. Время жизни Tэксп возбужденного состоянии ядра определяется многими физическими факторами, связанными со структурой ядра, а также
- 29. Мультипольное излучение порядка L (обычно его обозначают как 2L - польное, L = 1 соответствует дипольному,
- 30. Сохранение момента количества движения L приводит к следующим правила отбора по спинам: | Ii – If
- 31. Парциальные периоды полураспада В соответствии с правилами отбора эти излучения должны относится к разным типам. В
- 32. “Чистый” γ-переход Для “чистого” σL=EL или σL= M(L+1) γ-перехода значение парциального периода полураспада - τγ ,
- 33. Парциальные вероятности разрядки возбуждённых состояний атомных ядер. Парциальные вероятности B(σL) ≡ 1/τγ(σL) Парциальные вероятности для электрических
- 34. Парциальные вероятности для электрических M(L+1) переходов B(M(L+1) :
- 35. Парциальные вероятности разрядки возбуждённых состояний атомных ядер B(EL) и B(M(L+1)) позволяют : ● факторы запрета F
- 36. Мультипольность электромагнитных переходов задание Чётность : + π=1; – π = -1» σL σL σL 2+
- 38. Скачать презентацию







![Метод наклона. Уравнение приводит к следующим dF(t)/dt = -λ[F(t)-P(t)] d/dt[lnF(t)] = -λ[1-](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/978663/slide-19.jpg)













 Обмен веществ и энергии
Обмен веществ и энергии Тропики. Клуб Подружка
Тропики. Клуб Подружка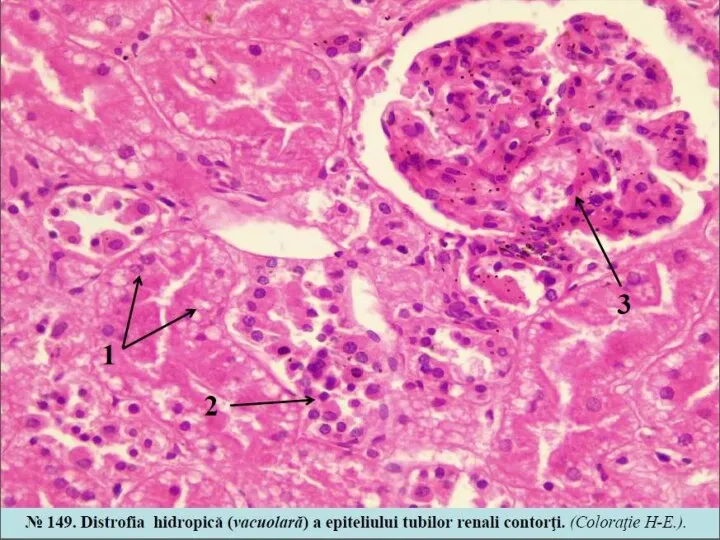 Mecanismul morfogenetic predominant al steatozei zonelor periferice
Mecanismul morfogenetic predominant al steatozei zonelor periferice Лунтик и его друзья в школе
Лунтик и его друзья в школе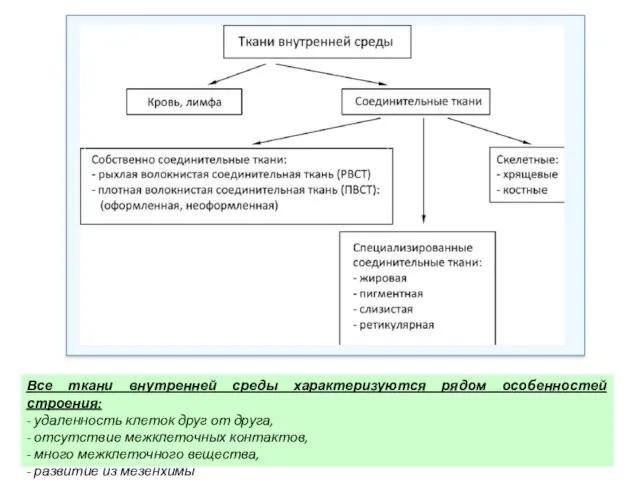 Ткани внутренней среды
Ткани внутренней среды Регуляция процессов жизнедеятельности организма
Регуляция процессов жизнедеятельности организма Биологические часы “сон-бодрствование” для человека
Биологические часы “сон-бодрствование” для человека Дыхание
Дыхание Формирование метапредметных результатов школьников при реализации ФГОС ООО по биологии
Формирование метапредметных результатов школьников при реализации ФГОС ООО по биологии Особенности применения метода близнецов
Особенности применения метода близнецов Возрастные изменения человека
Возрастные изменения человека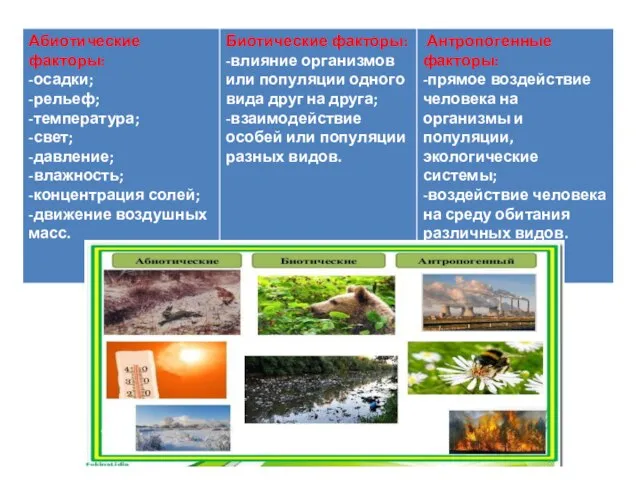 Факторы среды и их влияние на биоценозы (7 класс)
Факторы среды и их влияние на биоценозы (7 класс) Кожа и её производные
Кожа и её производные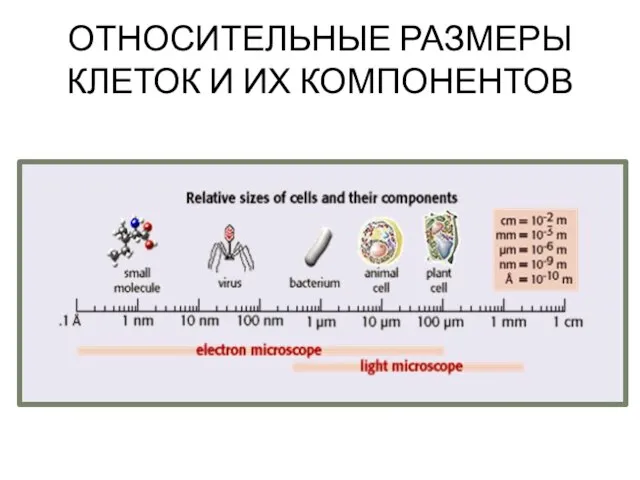 Относительные размеры клеток и их компонентов
Относительные размеры клеток и их компонентов Внутреннее строение листа. 6 класс
Внутреннее строение листа. 6 класс Презентация на тему Состав почвы
Презентация на тему Состав почвы  Презентация на тему СРЕДЫ ЖИЗНИ И МЕСТА ОБИТАНИЯ ЖИВОТНЫХ
Презентация на тему СРЕДЫ ЖИЗНИ И МЕСТА ОБИТАНИЯ ЖИВОТНЫХ  Терек табигать торлелеге. Патшалыклар
Терек табигать торлелеге. Патшалыклар 06 __________
06 __________ Belki
Belki Современные представления о структуре дыхательного центра
Современные представления о структуре дыхательного центра Хищные млекопитающие. Часть 2. Семейство кошачьи
Хищные млекопитающие. Часть 2. Семейство кошачьи Проводящие ткани и проводящие пучки
Проводящие ткани и проводящие пучки Бактерии
Бактерии Топография органов шеи
Топография органов шеи Строение стебля травянистых растений
Строение стебля травянистых растений Анализы. Глюкоза и метаболиты углеводного обмена
Анализы. Глюкоза и метаболиты углеводного обмена Доказательства эволюции органического мира
Доказательства эволюции органического мира