Содержание
- 2. существуют среды, используемые при решении разных задач: генетических исследований, при обработке штаммов мутагенами; селекции мутантов —
- 3. Выбор критерия оптимизации (применительно к средам в колбах) количество целевого продукта; производительность по целевому продукту; выход
- 4. Выбор исходных компонентов среды При подборе сред в первую очередь следует обратить внимание на химический состав
- 5. Определение соотношения компонентов среды . Рецептуры сред для промышленных штаммов охраняются как большой секрет, и многие
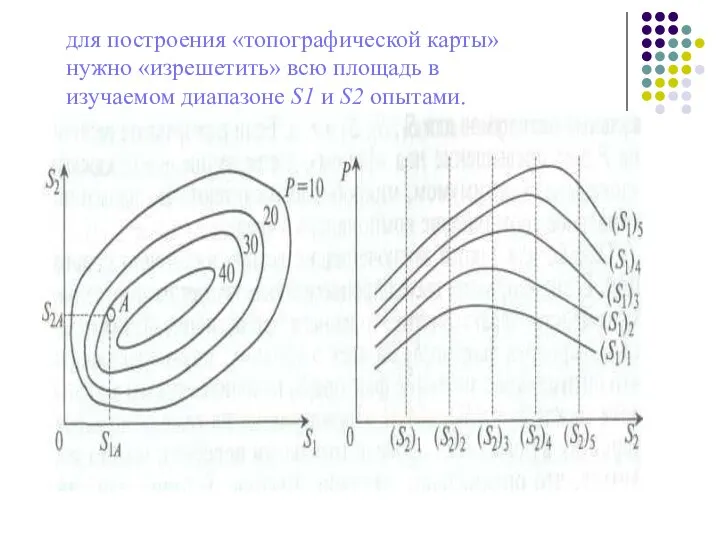
- 6. ТРАДИЦИОННЫЕ МЕТОДЫ ИЗУЧЕНИЯ МНОГОФАКТОРНЫХ ЗАВИСИМОСТЕЙ Необходимо построить поверхность отклика, напоминающую топографическую карту. На этой карте на
- 7. для построения «топографической карты» нужно «изрешетить» всю площадь в изучаемом диапазоне S1 и S2 опытами.
- 8. Отдельное изучение каждого фактора. при подборе сред микробиологи применяют исходный «фон» — определенное соотношение уровней факторов
- 9. Метод Гаусса — Зайделя этот метод называют «последовательным изучением каждого фактора». Здесь частные зависимости Р (S1),
- 10. Недостатки метода: метод Гаусса — Зайделя следует повторять пока частные оптимумы по отдельным факторам не перестанут
- 11. Процедура оптимизации по методу Гаусса-Зайделя
- 12. МЕТОД БОКСА — УИЛСОНА По этому методу вблизи исходной точки («фона») ставится специальным образом спланированная небольшая
- 13. Процедура оптимизации по методу Бокса-Уилсона
- 14. Исследовательская серия опытов сначала ставится небольшая серия опытов на двух уровнях — верхнем и нижнем. Для
- 15. Для чего ставится исследовательская серия опытов? Чтобы получить линейное уравнение, связывающее выходной параметр оптимизации Р с
- 16. для упрощения расчетов по методу Бокса—Уилсона опыты ставят не при произвольным образом измененных значениях уровней разных
- 17. Свойства матрицы: 1. в каждой серии количество вариантов опытов с верхним уровнем каждого фактора равно количеству
- 18. Планы ортогональных матриц разработаны для различного числа факторов n и могут включать разное число вариантов планирования.
- 19. Планы экспериментов имеются в различных справочниках и руководствах.
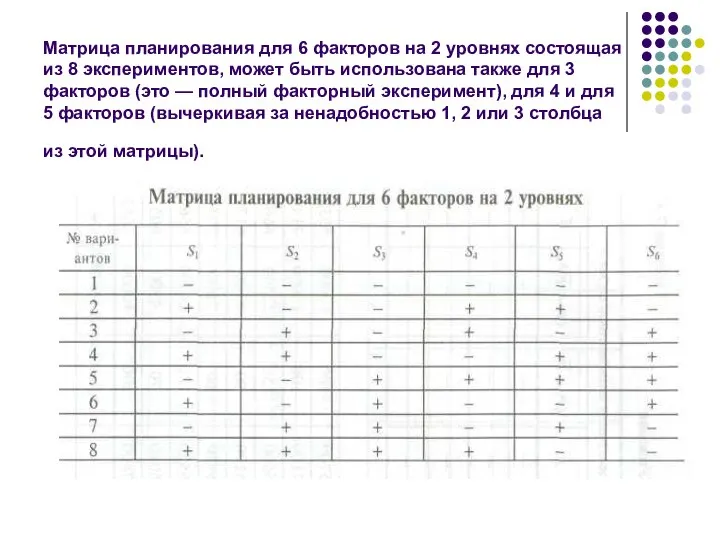
- 20. Матрица планирования для 6 факторов на 2 уровнях состоящая из 8 экспериментов, может быть использована также
- 21. После выбора матрицы планирования, числа варьируемых факторов и интервалов планирования можно переходить от условных обозначений матриц,
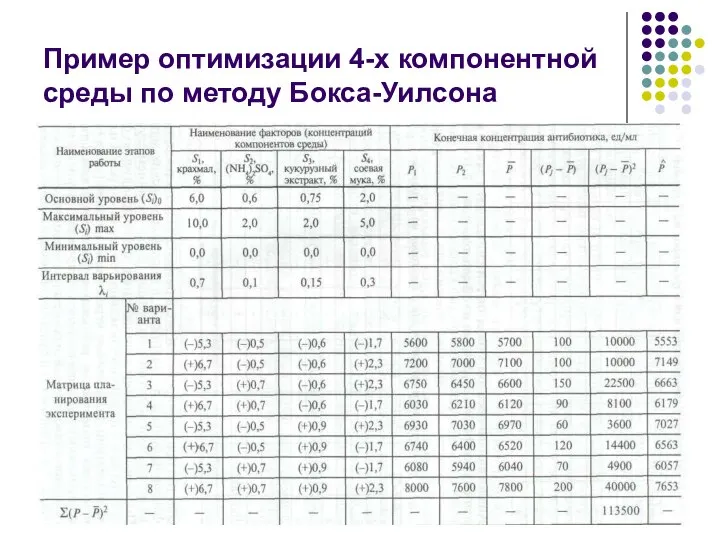
- 22. Пример оптимизации 4-х компонентной среды по методу Бокса-Уилсона
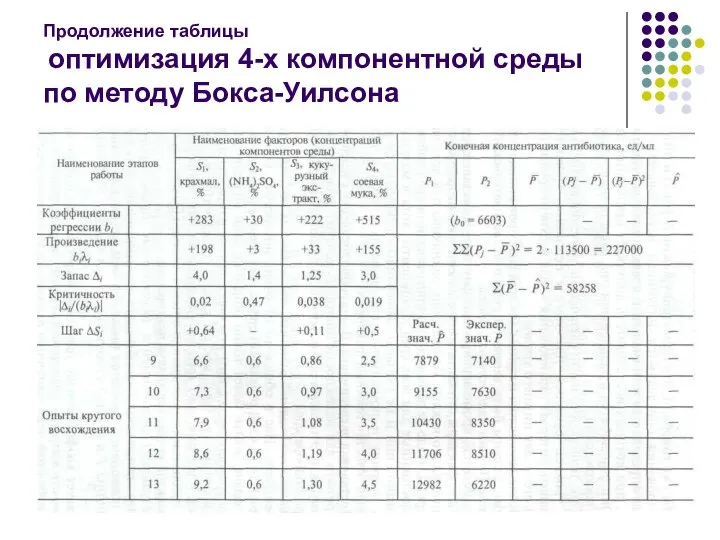
- 23. Продолжение таблицы оптимизация 4-х компонентной среды по методу Бокса-Уилсона
- 24. оптимизация среды по методу Бокса-Уилсона После выбора матрицы планирования, числа варьируемых факторов и интервалов планирования можно
- 25. МАТЕМАТИЧЕСКИЕ ПРОЦЕДУРЫ В МЕТОДЕ БОКСА—УИЛСОНА основной уровень («фон»), интервалы варьирования, минимальный и максимальный уровни фактора, при
- 26. МАТЕМАТИЧЕСКИЕ ПРОЦЕДУРЫ В МЕТОДЕ БОКСА—УИЛСОНА кроме варьируемых факторов в составе среды могут быть факторы, значение которых
- 27. Постановка эксперимента В микробиологических исследованиях принято для надежности повторять опыты и не по одному разу. Это
- 28. Расчет коэффициентов уравнения регрессии Свободный член уравнения bо находится как среднее из значений Р для всех
- 29. Коэффициент регрессии i-го фактора определяется как разность сумм выходов Ри, в которых фактор Si, находился со
- 30. Если принять кодированные значения факторов Xi т.е. Siu, как (+1) для верхнего уровня и (—1) для
- 31. Например, для фактора S2 в таблице коэффициент регрессии вычисляют следующим образом:
- 32. Рассчитанные таким образом коэффициенты имеют разные знаки. Знак (+) означает, что при увеличении данного фактора происходит
- 33. На основе коэффициентов регрессии можно записать уравнение Чтобы перейти к натуральным переменным, нужно подставить выражение для
- 34. Определение запаса для движения в направлении крутого восхождения При определении программы крутого восхождения от основного уровня
- 35. Определение вспомогательного показателя «критичность». Этот показатель представляет собой модуль отношения запаса ∆i, и произведения biλi,- и
- 36. Выбор шага крутого восхождения Обычно крутое восхождение проводится путем равномерного пошагового приращения в каждом последующем опыте
- 37. Выбор шага крутого восхождения Обычно выбирают относительно немного шагов в направлении крутого восхождения: 5—8, не более.
- 38. Выбор шага крутого восхождения Если величина базового шага равна 0,5,то пропорционально произведениям biλi,- найдем величину шага
- 39. Для фактора проставлен прочерк. Значит по результатам анализа установлено, что данный фактор не оказывает существенного влияния
- 40. СТАТИСТИЧЕСКАЯ ОЦЕНКА РЕЗУЛЬТАТОВ В биологических процессах результат процесса обычно неоднозначен. Существует какой-то уровень колебаний, возможных по
- 41. коэффициенты регрессии определяют по значениям выходного показателя, для них есть уровень случайных изменений, который находят с
- 42. Первый способ— многократное повторение опытов для одного и того же варианта (среды). В этом случае имеем
- 43. Дисперсию воспроизводимости определяют по формуле: Это не среднеквадратичное отклонение, а дисперсия воспроизводимости каждого отдельного измерения.
- 44. Если выполнить несколько серий опытов на одной и той же среде (в каждой серии число опытов
- 45. Второй способ— расчет дисперсии процесса по данным повторных экспериментов матрицы планирования. Он более удобен при планировании
- 46. Надежность вычисления дисперсии воспроизводимости определяется количеством «лишних» опытов, необходимых для нахождения дисперсии. Количество «лишних» опытов называют
- 47. для надежного определения дисперсии воспроизводимости процесса число степеней свободы f должно быть не менее 5—8. Чем
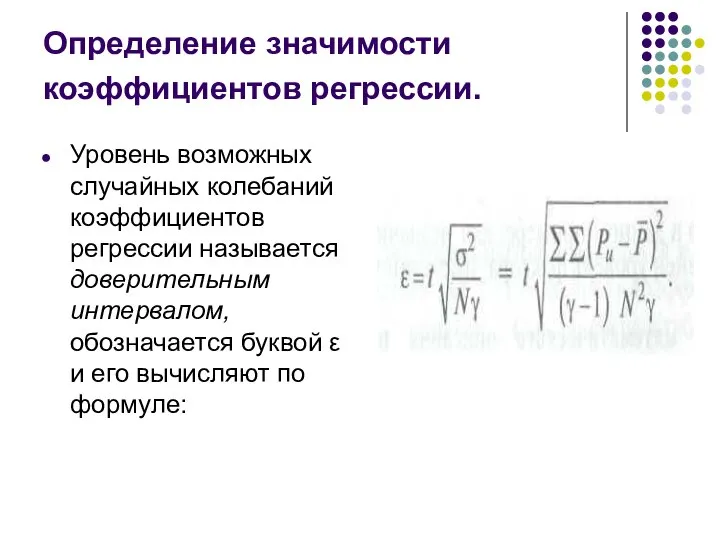
- 48. Определение значимости коэффициентов регрессии. Уровень возможных случайных колебаний коэффициентов регрессии называется доверительным интервалом, обозначается буквой ε
- 49. В этой формуле появляется новый коэффициент t — критерий Стьюдента, определяемый по таблицам. Для надежности оценки
- 50. значения критерия Стьюдента для наиболее часто встречающихся значений f при Р = 0,95: вначале критерий t
- 51. Доверительный интервал ε имеет одно и то же значение для всех коэффициентов bi (в кодированном виде).
- 52. Незначимость коэффициентов может быть вызвана различными причинами: 1. взяты слишком малые интервалы варьирования фактора; 2. плохая
- 53. Адекватность математического описания процесса Кроме оценки значимости коэффициентов в процедуре статистического анализа предусмотрена оценка адекватности полученного
- 54. для варианта 6 величину Р можно определить так
- 55. Дисперсия адекватности определяется по формуле где n — число факторов в уравнении; N — число вариантов
- 56. Знаменатель этой дроби представляет собой число степеней свободы fа дисперсии адекватности: fa = N - n
- 57. Чтобы найти адекватность уравнения, необходимо критерий Фишера сравнить с табличным FT, имеющимся в справочниках по статистике,
- 58. Расчет программы крутого восхождения Для данного примера рассчитывают условия для 6 шагов крутого восхождения, т. е.
- 59. Анализ результатов крутого восхождения сначала нужно все значения уровней факторов пересчитать в кодированные. затем рассчитать величину
- 60. В колонке рядом с расчетными данными указать экспериментальные. Часто столь высоких значений выхода, как ожидали, не
- 61. расчет по этому методу необходимо повторять до тех пор, пока линейное уравнение не станет неадекватным. В
- 62. МНОГОУРОВНЕВЫЕ ПЛАНЫ ЭКСПЕРИМЕНТА методом является аддитивно-решетчатое описание процесса. В этом случае объект описывается аддитивно-нелинейным решетчатым уравнением:
- 63. Аддитивное — значит состоящее из суммы членов, каждый из которых зависит только от одного из факторов.
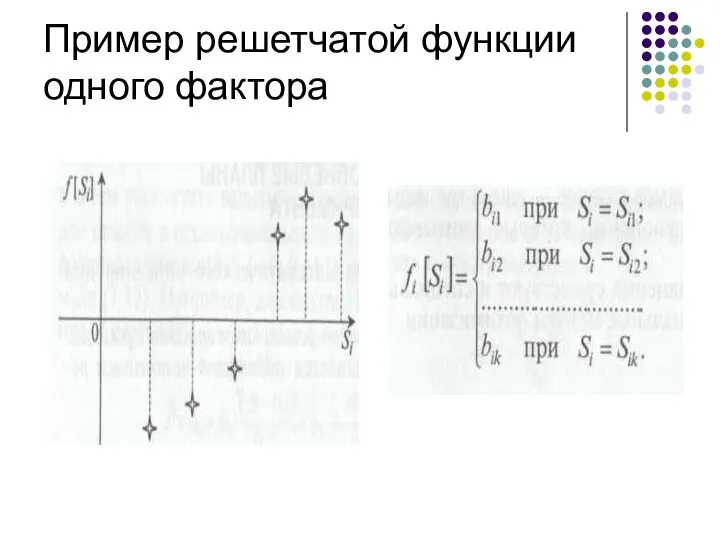
- 64. Пример решетчатой функции одного фактора
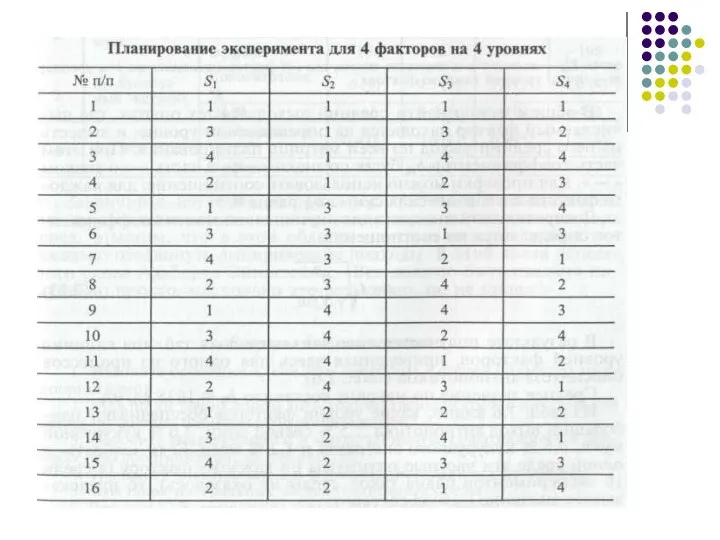
- 65. Чтобы получить зависимости с наименьшим числом опытов и упростить вычисления, целесообразно использовать ортогональные матрицы планирования уже
- 66. На практике такие схемы планирования эксперимента называют схемами ортогональных латинских прямоугольников (или квадратов, если число факторов
- 68. Величина эффектов решетчатого описания (bik) и значение bо рассчитываются почти так же просто, как в методе
- 69. нужно найти средний выход Р в тех опытах, где вычисляемый фактор находится на определяемом уровне, вычесть
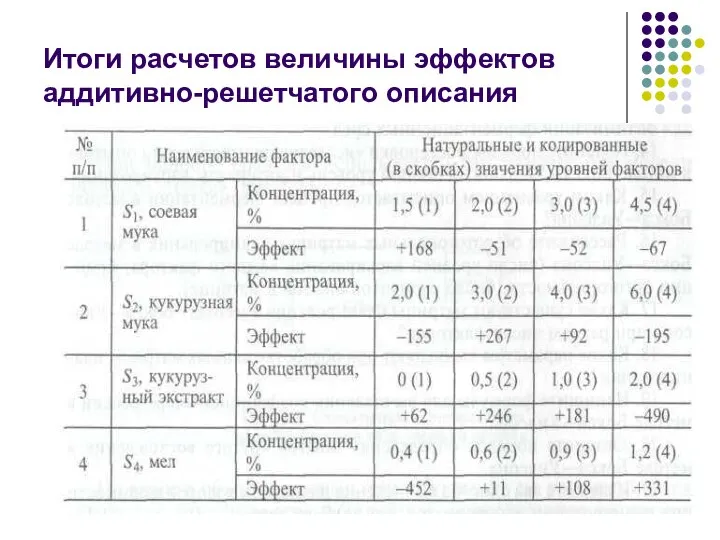
- 70. Итоги расчетов величины эффектов аддитивно-решетчатого описания
- 71. Адекватность аддитивно-решетчатого описания проверяют аналогично методу Бокса—Уилсона. При нахождении дисперсии адекватности число степеней свободы fa принимают
- 73. Скачать презентацию






























































 Поиск оптимальных условий непосредственно в процессе выращивания микроорганизмов
Поиск оптимальных условий непосредственно в процессе выращивания микроорганизмов Сенсорные системы. Зрительный анализатор
Сенсорные системы. Зрительный анализатор Воздушное питание. Фотосинтез
Воздушное питание. Фотосинтез Биология раневого процесса
Биология раневого процесса Структурная организация клеток прокариот и эукариот. Лекция 1
Структурная организация клеток прокариот и эукариот. Лекция 1 Толстая кишка
Толстая кишка Побе́г (лат. córmus) — один из основных вегетативных органов высших растений
Побе́г (лат. córmus) — один из основных вегетативных органов высших растений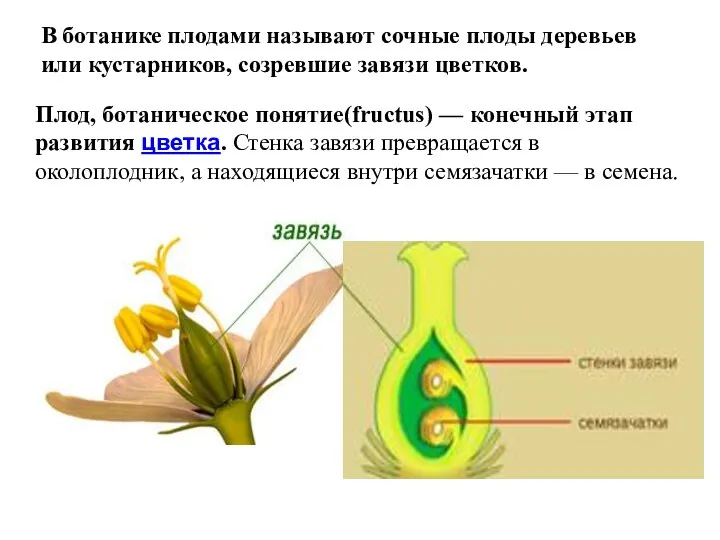 SVEZhIE_PLODY
SVEZhIE_PLODY Орталық жүйке жүйесінің құрылысы мен қызметі
Орталық жүйке жүйесінің құрылысы мен қызметі Характеристика царства Растения
Характеристика царства Растения У кого из животных есть мантия. Итоговый тест
У кого из животных есть мантия. Итоговый тест Презентация на тему Соцветия. Виды соцветий
Презентация на тему Соцветия. Виды соцветий  Взаимодействие между видами: конкуренция
Взаимодействие между видами: конкуренция Систематическое положение человека (8)
Систематическое положение человека (8) Анализ состава гетерозиготных генотипов CYP2C19 для определения цис- и трансконфигурации
Анализ состава гетерозиготных генотипов CYP2C19 для определения цис- и трансконфигурации 3. Урок - РНК и АТФ
3. Урок - РНК и АТФ Селекция растений и животных
Селекция растений и животных Типы развития насекомых
Типы развития насекомых Как зимой помочь птицам? Следы на снегу
Как зимой помочь птицам? Следы на снегу Способы движений растений
Способы движений растений Дробление
Дробление Анатомия, физиология и патология зрительного анализатора
Анатомия, физиология и патология зрительного анализатора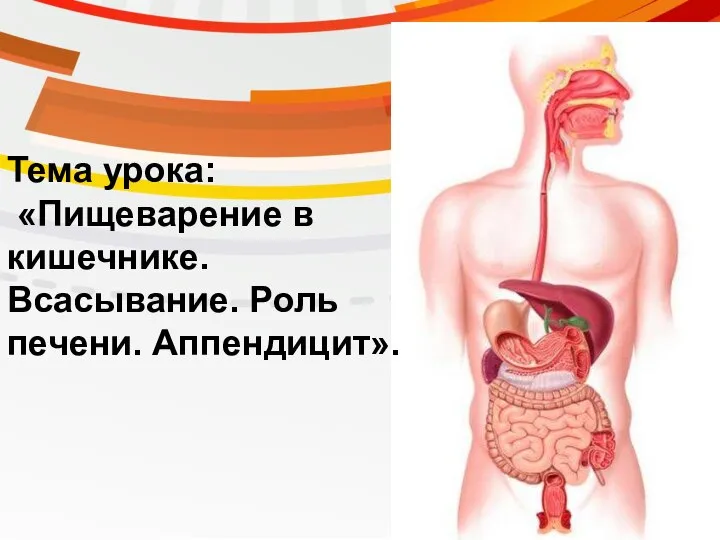 Пищеварение в кишечнике. Всасывание. Роль печени. Аппендицит
Пищеварение в кишечнике. Всасывание. Роль печени. Аппендицит Водорастворимые витамины
Водорастворимые витамины Презентация на тему Рациональное использование и охрана животных
Презентация на тему Рациональное использование и охрана животных  Сон и сновидения
Сон и сновидения Летучая мышь (фото)
Летучая мышь (фото) Животные на службе у человека
Животные на службе у человека