Сравнительный анализ алгоритмов, вычисляющих расстояния последовательностей ДНК и некоторые связанные проблемы

Задача сравнения схожести строковых последовательностей ДНК
За последние годы были описаны различные подходы к определению схожести последовательностей ДНК. Каждый из таких подходов определяет множество значений которое необходимо нуждается в качественной оценке…..
ATCGCGTCGAAACGCGCGTCGAACGCGCGTCGAACGCGTCGAA….
ATCGCGTCGAAACGCGCGTCGAACGCGCGTCGAACGCGTCGAA….
ДНК№1
ДНК№2

Качественная оценка алгоритмов
В настоящей статье предлагается новый подход к решению этой задачи, причём алгоритмы для его реализации выполнены на основе ранее разработанного нами мультиэвристического подхода к задачам дискретной оптимизации. Однако основным предметом данной статьи является описание нашего оригинального подхода к сравнению качества определяемых метрик на множестве последовательностей ДНК. Последний подход основан на том, что тройки расстояний между геномами в идеале должны образовывать равнобедренные остроугольные треугольники.

Алгоритмы для качественного
сравнения
1) Мультиэвритический алгоритм
2) Расстояние Джаро-Винклера
3) Расстояние Хэмминга
4) Расстояние Дамерау — Левенштейна
5) метрика Смита-Вотермана

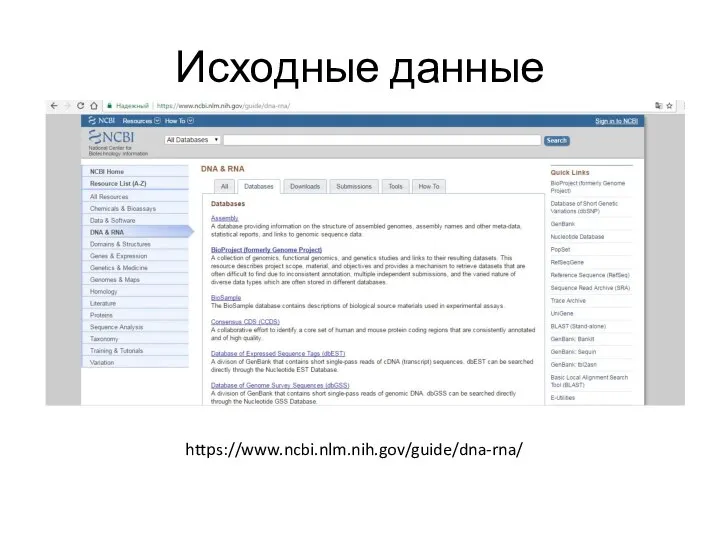
Исходные данные
https://www.ncbi.nlm.nih.gov/guide/dna-rna/

Результаты вычислений.
Матрица расстояний 100X100
Матрица расстояний рассматривается как метрическое пространство

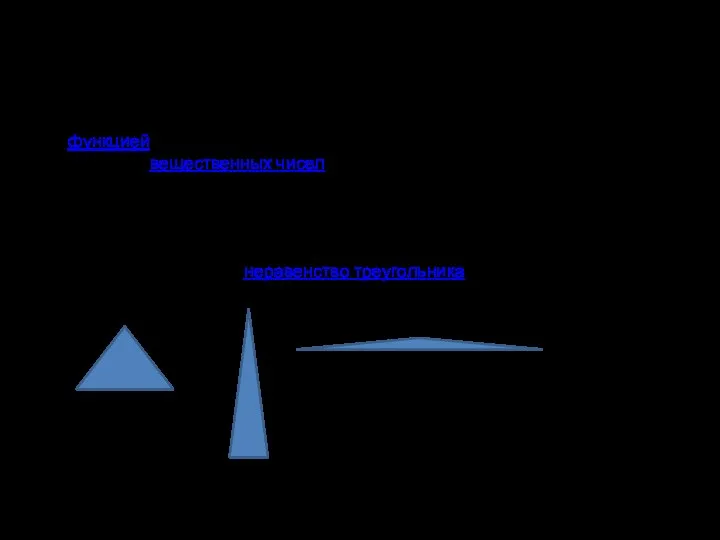
Метрическое пространство
Метрическое пространство M есть множество точек с функцией расстояния (также называется метрикой) (где обозначает множество вещественных чисел). Для любых точек x, y, z из M эта функция должна удовлетворять следующим условиям:
d(x, y) ≥ 0
d(x, y) = 0 x = y.
d(x, y) = d(y, x) (симметрия)
d(x, z) ≤ d(x, y) + d(y, z) (неравенство треугольника).

Bedness
Итак, мы в простых случаях будем считать badness (норму) всей матрицы расстояний суммой, а для badness каждого треугольника будем применять один из следующих 4 вариантов. (Всюду считаем, что в рассматриваемом треугольнике стороны – a, b и c, причём a ≥ b ≥ c; углы – α, β и γ, причём α ≥ β ≥ γ.)
(α–β) / π.
(α–β) / α.
(a–b) / a.
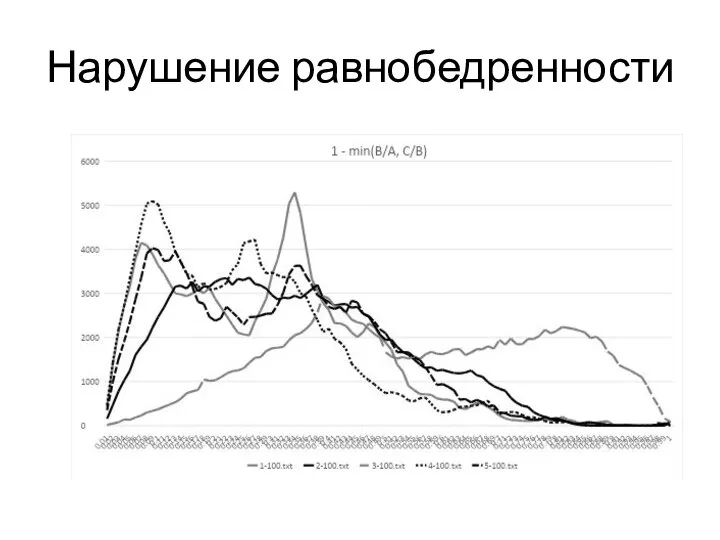
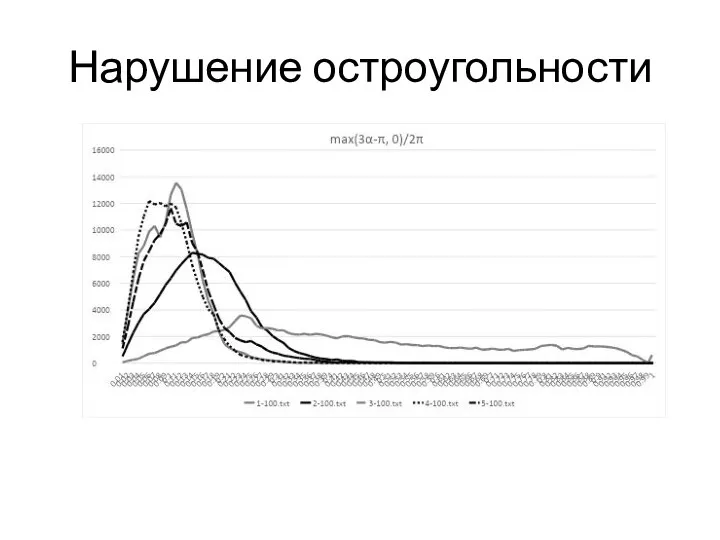
В последней норме «нарушение равнобедренности» и «нарушение остроугольности» рассмотрим отдельно:
(A) 1 – min (b/a, c/b) ;
(B) max (3 α– π, 0) / (2π) ;
общий ответ – (A+B) / 2 .
При этом максимальное значения badness (в каждом из этих 4 случаев) для некоторого треугольника может быть равно 1. В самом же плохом случае работы алгоритмов построения метрики – т.е. при возникающем нарушении неравенства треугольника – мы полагаем это значение равным от 1 до 2 (также в зависимости от количественных характеристик этого нарушения).
Отметим заранее, что мы иногда рассматриваем и несколько более сложные варианты, которые, однако, в настоящей статье не описаны.

Нарушение равнобедренности

Нарушение остроугольности