Слайд 2Вопросы для повторения
1. Что называют призмой ?
2. На рисунке показать основания, боковые

грани, ребра, вершины, высоту, диагональ призмы.
3. Какая призма называется правильной ?
4. Что называют диагональным сечением ?
Слайд 4Определение
Площадью полной поверхности призмы называется сумма площадей всех её граней
Sп.п

Слайд 5Определение
Площадью боковой поверхности призмы называется сумма площадей всех её боковых граней
Sбок

Слайд 6Обозначения
Sп.п - площадь полной поверхности
Sбок - площадь полной поверхности
Sосн -площадь полной

поверхности
Слайд 9Теорема
Площадь боковой поверхности прямой призмы равна произведению
периметра основания на высоту
(

длину бокового ребра)
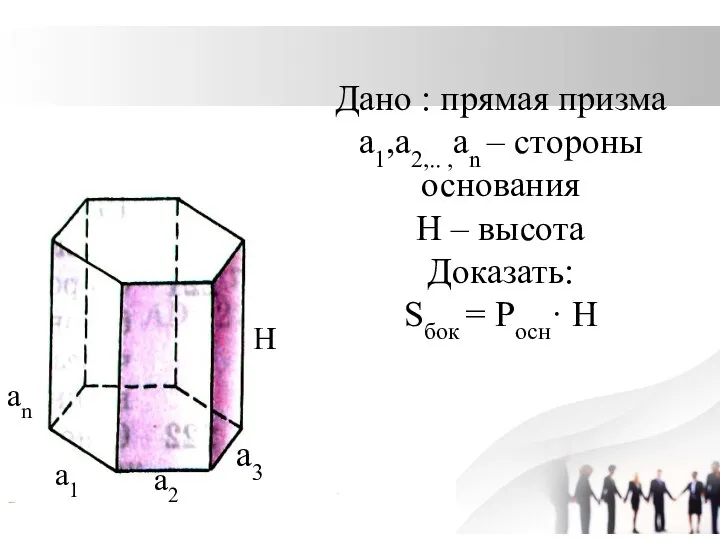
Слайд 10Дано : прямая призма
а1,а2,.. ,аn – стороны
основания
Н – высота
Доказать:
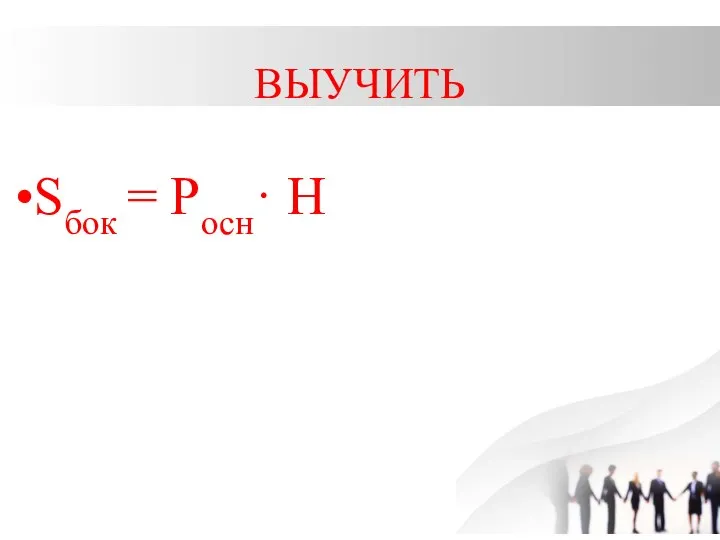
Sбок = Росн·
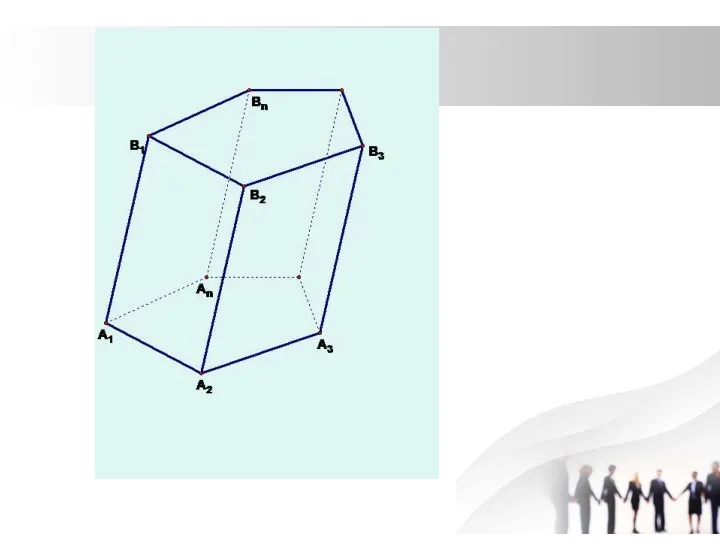
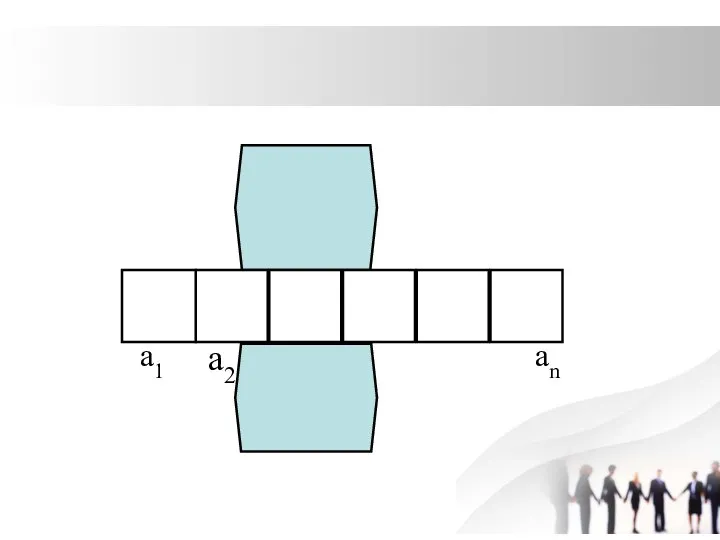
Слайд 11Доказательство:
Боковые грани прямой призмы –
прямоугольники
Sбок = S1 + S2+ S3

+ … + Sn =
= а1Н + а2Н + а3Н + … +аnН =
= (а1+ а2+ а3 + … +аn) Н =
= Росн· Н
Ч. т. д
Слайд 13Решить задачу
В правильной
n – угольной призме сторона
основания равна

а и боковое ребро Н. Вычислите площадь полной поверхности призмы, если :
а) n= 4, а = 10 см, Н = 15см,
б) n = 3, а = 12см, Н = 8 см.
Слайд 16Найти площадь полной поверхности прямой призмы, основанием которой служит параллелограмм со сторонами

5 и 10 см, угол между ними 600
Высота призмы 20 см
Слайд 17Экзаменационная задача
Основанием прямой призмы является равнобедренный прямоугольный треугольник. Большая боковая грань- квадрат

со стороной 6√2 см.Найдите площадь полной поверхности призмы










 Пропорция
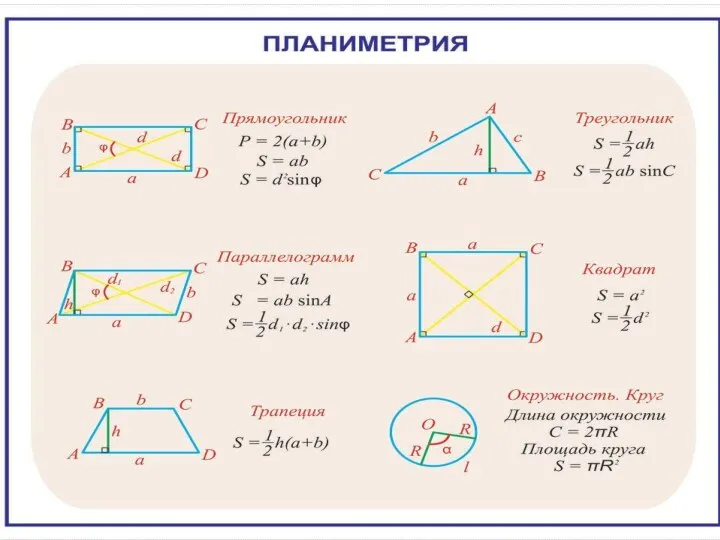
Пропорция Измерение площадей. Площадь прямоугольника
Измерение площадей. Площадь прямоугольника Графики линейных функций
Графики линейных функций Центральные и вписанные углы
Центральные и вписанные углы English System of Measures
English System of Measures Функции многих переменных. Лекция 16
Функции многих переменных. Лекция 16 Геометрические преобразования в пространстве
Геометрические преобразования в пространстве История происхождения математических знаков
История происхождения математических знаков Решение тригонометрических уравнений
Решение тригонометрических уравнений بخش دوم :حل معادله درجه 2و کاربرد آن ریاضی دهم آنسانی
بخش دوم :حل معادله درجه 2و کاربرد آن ریاضی دهم آنسانی Статистика
Статистика Начерти два отрезка
Начерти два отрезка Теория вероятностей
Теория вероятностей Единица времени - секунда
Единица времени - секунда Измерение углов, расстояний. Теодолит, устройство, поверки (лекция 5)
Измерение углов, расстояний. Теодолит, устройство, поверки (лекция 5) Решение задач на временные отношения (подготовка к олимпиаде по математике обучающихся 4 класса)
Решение задач на временные отношения (подготовка к олимпиаде по математике обучающихся 4 класса) ПГНИУ-20.09.22 МЛ Л 4
ПГНИУ-20.09.22 МЛ Л 4 Геометрические фигуры (открытый урок - игра Поле чудес)
Геометрические фигуры (открытый урок - игра Поле чудес) Интегральное исчисление
Интегральное исчисление Великие математики
Великие математики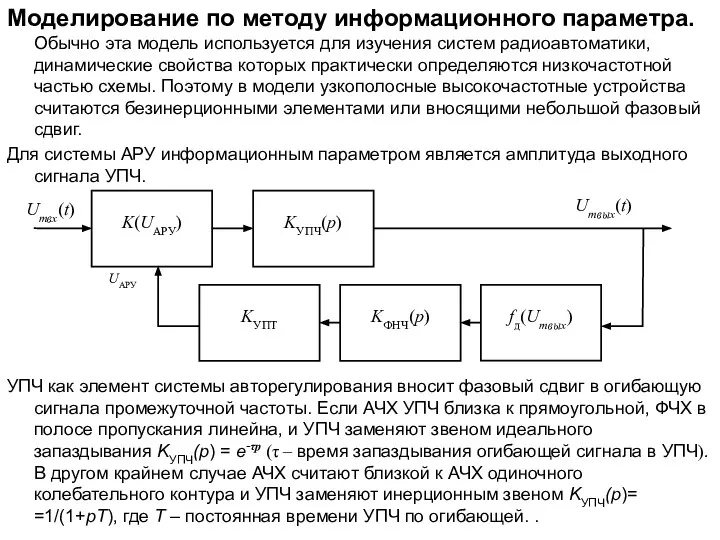 Моделирование по методу информационного параметра
Моделирование по методу информационного параметра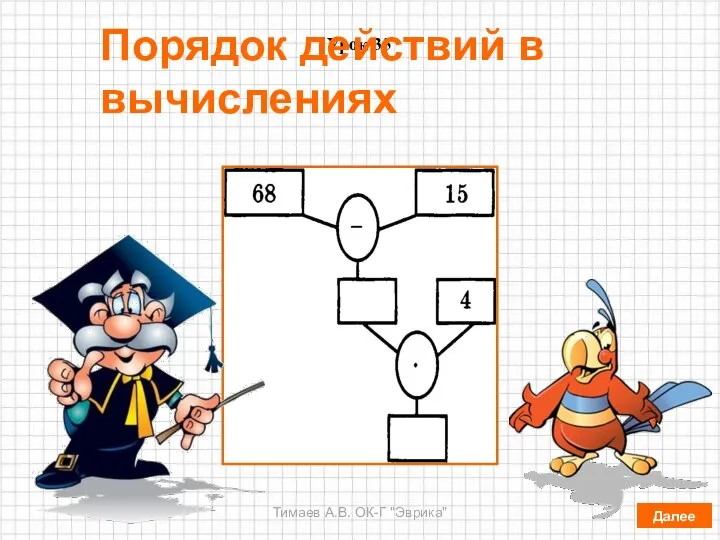 Порядок действий в вычислениях
Порядок действий в вычислениях Четырехугольники
Четырехугольники Сечения параллелепипеда
Сечения параллелепипеда Геометрические фигуры
Геометрические фигуры Линейные уравнения. Решение задач с помощью линейных уравнений. 7 класс
Линейные уравнения. Решение задач с помощью линейных уравнений. 7 класс Первообразная. Неопределенный интеграл и его свойства
Первообразная. Неопределенный интеграл и его свойства Признаки равенства треугольников
Признаки равенства треугольников