Математическое моделирование в экологии

Значения термина «модель»
1. Физическое (вещественно-натуральное) или знаковое (математическое) подобие (обычно упрощенное) реального объекта, явления или процесса;
2. Уменьшенное подобие реального объекта; отличают действующую модель и только имитирующую форму чего-то (макет);
3. Схема, изображение или описание какого-либо явления или процесса в природе и обществе.
В экологии модель – материальный или мысленно представляемый объект, который при исследовании замещает объект-оригинал, и его изучение дает новые знания об объекте-оригинале. Модель упрощает действительность, но ярко показывает элементы и связи интересные ученому.

Основные цели моделирования:
− изучение основных свойств объекта или явления: компактное описание наблюдений; анализ наблюдений (объяснение явлений);
− прогнозирование поведения объекта-оригинала в реальных условиях;
− создание эффективных систем управления объектом или процессом.
− обратная задача: когда об объекте исследования уже имеются необходимые знания, но их требуется передать другим – это тренажеры, стенды, энциклопедии.

Моделирование – метод исследования сложных объектов, явлений и процессов путем их упрощенного имитирования (натурного, математического, логического). Основывается на теории подобия (сходства) с объектом-аналогом.
Требования к моделям:
основное требование – адекватность реальным процессам или объектам, которые они моделируют;
увеличенное (клетка) или уменьшенное (глобус) подобие объекта;
замедляет быстро протекающие процессы или ускоряет медленно протекающие;
упрощает реальный процесс – возможность обратить внимание на главную сущность объекта.

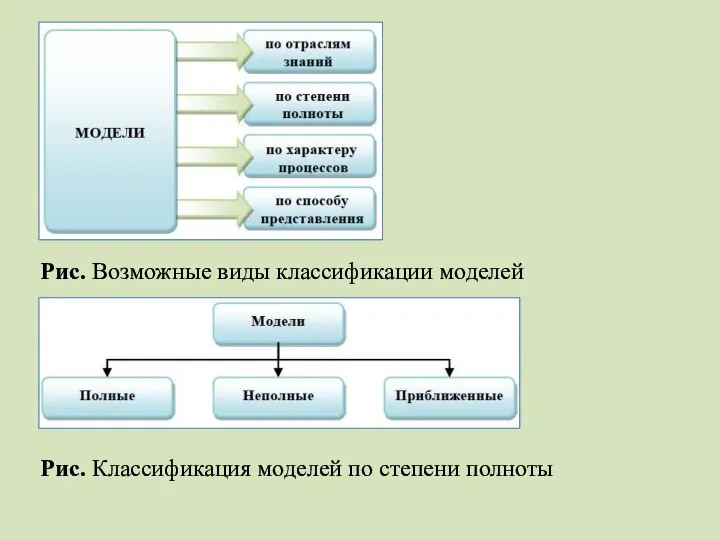
Рис. Возможные виды классификации моделей
Рис. Классификация моделей по степени полноты

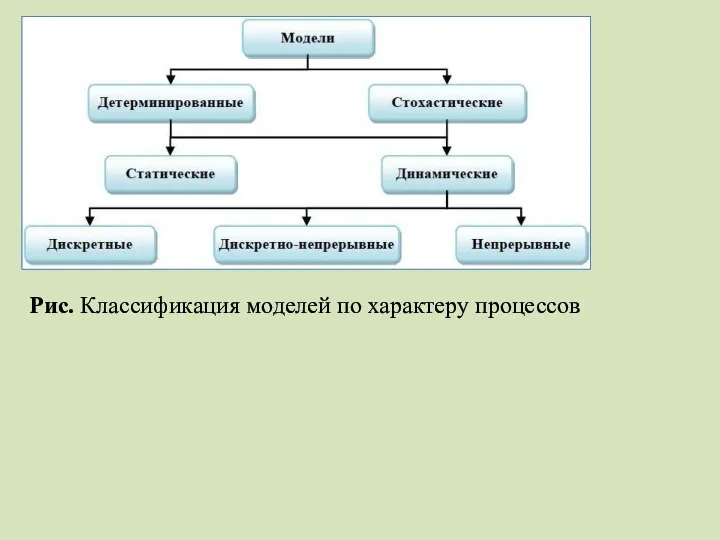
Рис. Классификация моделей по характеру процессов

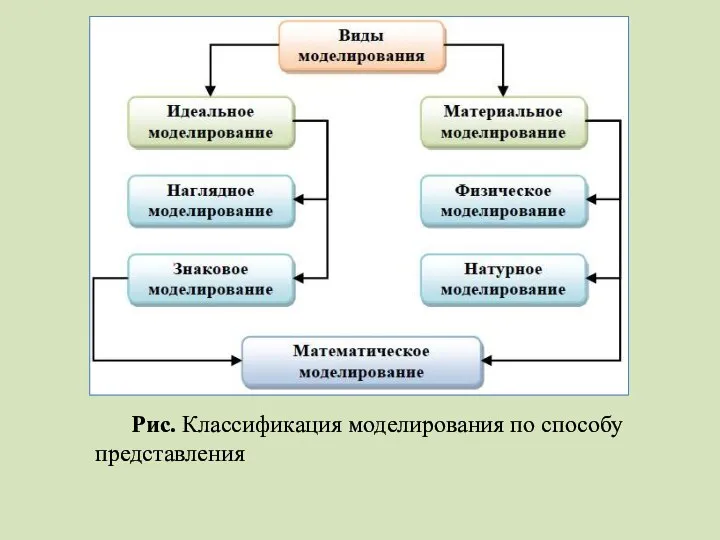
Рис. Классификация моделирования по способу представления

Основания для классификации моделей (продолжение)
- природа моделируемого объекта (наземные, водные, глобальные экосистемы) и уровень его детализации (клетка, организм, популяция и т.д.);
- используемый логический метод: дедукция (от общего к частному) или индукция (от частных, отдельных факторов к обобщающим);
- статический подход или анализ динамики временных рядов (последний, в свою очередь, может быть ретроспективным или носить прогнозный характер);
- используемая математическая парадигма (детерминированная и стохастическая).

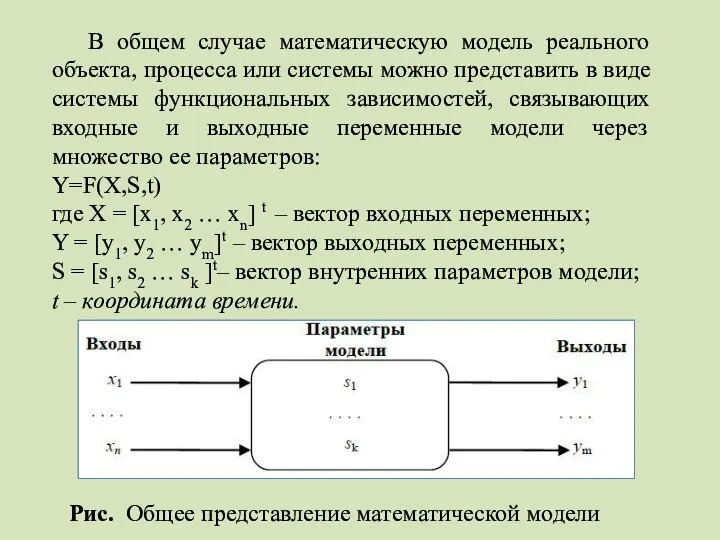
В общем случае математическую модель реального объекта, процесса или системы можно представить в виде системы функциональных зависимостей, связывающих входные и выходные переменные модели через множество ее параметров:
Y=F(X,S,t)
где X = [x1, x2 … xn] t ‒ вектор входных переменных;
Y = [y1, y2 … ym]t ‒ вектор выходных переменных;
S = [s1, s2 … sk ]t‒ вектор внутренних параметров модели;
t – координата времени.
Рис. Общее представление математической модели

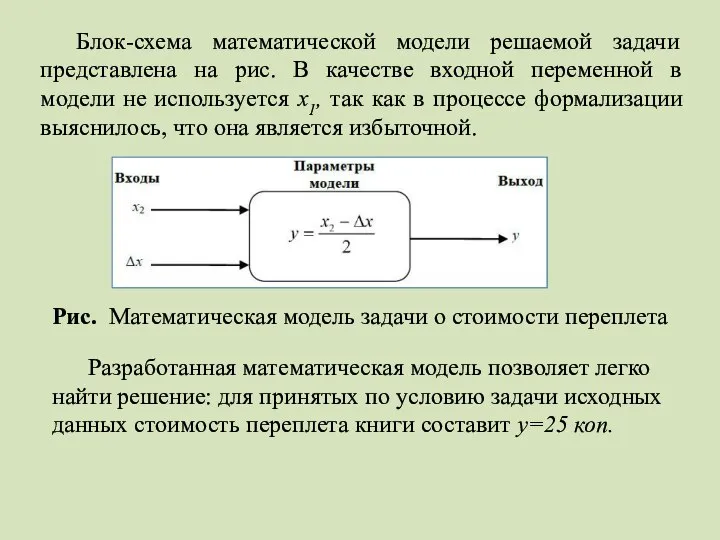
Пример: рассмотрим применение метода математического моделирования для решения простой математической задачи Я.И.Перельмана.
Задача. Книга в переплете стоит 2 руб. 50 коп. Книга на 2 руб. дороже переплета. Сколько стоит переплет?
Решение. Введем обозначение переменных:
х1 – стоимость книги без переплета;
х2 – стоимость книги с переплетом;
у – стоимость переплета;
Δх – разница в стоимости книги и переплета.
Проведем формализацию решаемой задачи и установим количественную связь между переменными (определим параметры модели). По условию задачи:
х1+у=х2
у+Δх=х1
После несложных преобразований получим характеристическое уравнение математической модели, связывающее входные и выходную переменные:
у=(х2‒Δх)/2

Блок-схема математической модели решаемой задачи представлена на рис. В качестве входной переменной в модели не используется х1, так как в процессе формализации выяснилось, что она является избыточной.
Рис. Математическая модель задачи о стоимости переплета
Разработанная математическая модель позволяет легко найти решение: для принятых по условию задачи исходных данных стоимость переплета книги составит у=25 коп.

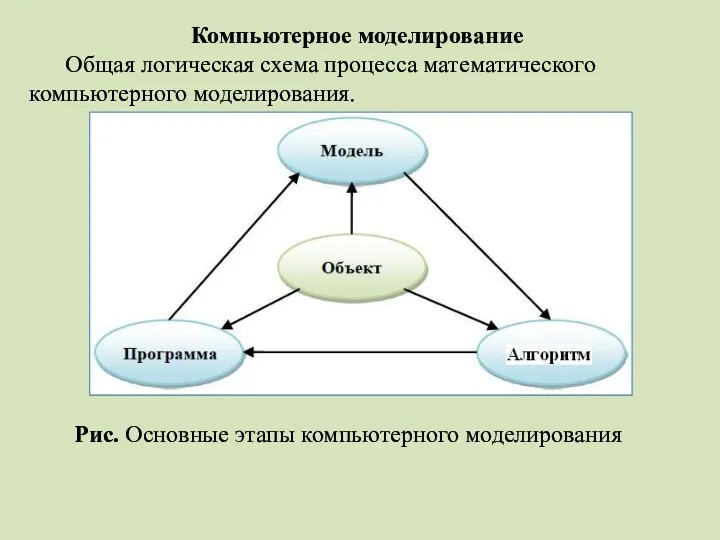
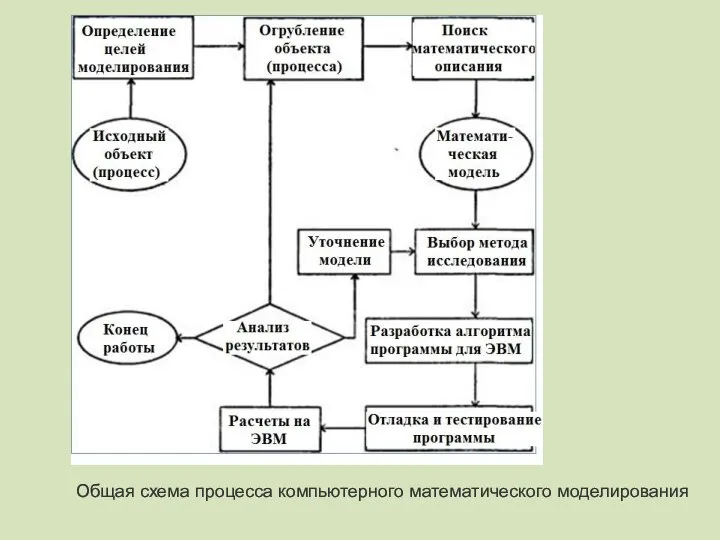
Компьютерное моделирование
Общая логическая схема процесса математического компьютерного моделирования.
Рис. Основные этапы компьютерного моделирования

Основные этапы технологии решения задач с помощью компьютерного моделирования:
1. постановка задачи;
2. математическая формализация;
3. разработка алгоритма;
4. составление программы или выбор среды программирования;
5. компьютерное моделирование.
1. Анализ объекта исследования: наиболее существенные черты и свойства. Устанавливаются упрощающие допущения, входные и выходные переменные, диапазон их возможного изменения, тип и структура переменных, форма выдачи результатов решения.
2. Строится математическая модель объекта исследования, отражающая в виде математических соотношений его основные свойства.

3. Алгоритм определяет последовательность действий, которые надо выполнить, чтобы от исходных данных перейти к искомым переменным. Не должны искажать основные свойства модели, быть экономичными и адаптирующимися к особенностям решаемых задач и используемых компьютеров.
4. Выбор языка и среды программирования и разработка компьютерной программы, или выбор готовой прикладной компьютерной программы, возможности и интерфейс которой позволяют исследовать математическую модель без написания программного кода.
5. Компьютерная программа тестируется в вычислительных экспериментах, результат которых достоверно известен. В случае необходимости математическая модель, алгоритм и программа корректируются и уточняются. Затем проводятся необходимые эксперименты с целью получения искомых результатов.

Требования к математическим моделям
Наиболее важные: точность, универсальность и экономичность.
Точность модели – это количественная оценка степени совпадения модельных результатов с действительными.

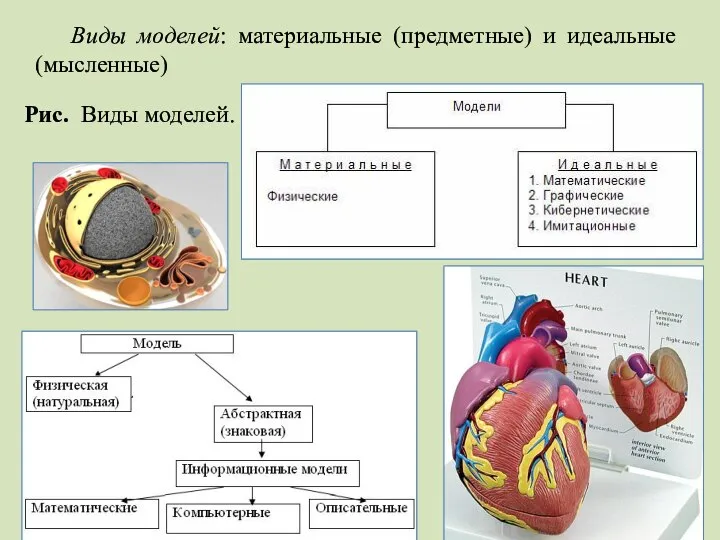
Виды моделей: материальные (предметные) и идеальные (мысленные)
Рис. Виды моделей.

Из материальных – физические модели. При строительстве ГЭС строятся уменьшенные модели устройств и сооружений.
Математические, кибернетические, имитационные, графические модели. Суть: с помощью математических символов строится абстрактное упрощенное подобие изучаемой системы. Меняя значение отдельных параметров, исследуют, как поведет себя данная искусственная система, т. е. как изменится конечный результат.

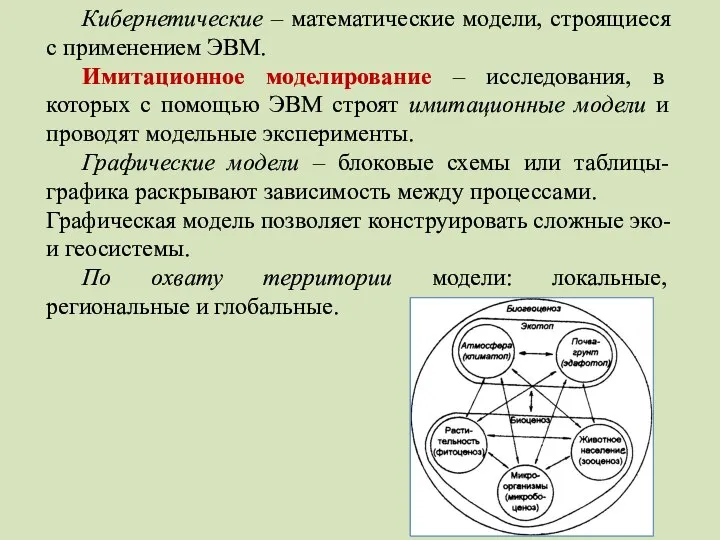
Кибернетические – математические модели, строящиеся с применением ЭВМ.
Имитационное моделирование – исследования, в которых с помощью ЭВМ строят имитационные модели и проводят модельные эксперименты.
Графические модели – блоковые схемы или таблицы-графика раскрывают зависимость между процессами. Графическая модель позволяет конструировать сложные эко- и геосистемы.
По охвату территории модели: локальные, региональные и глобальные.

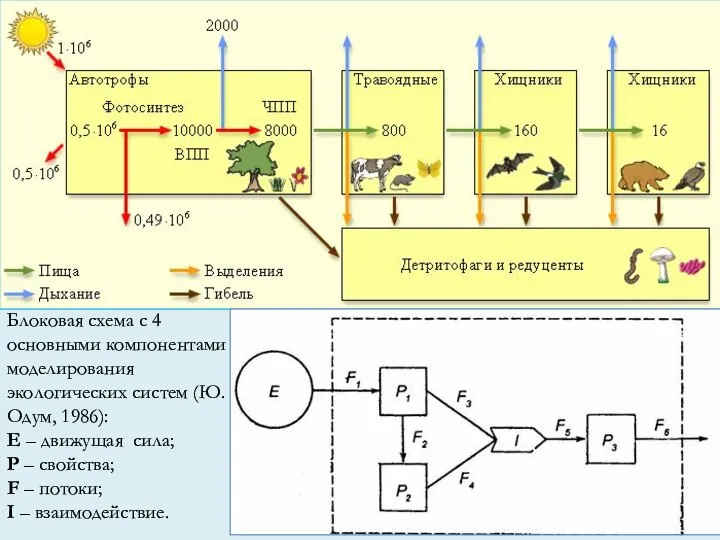
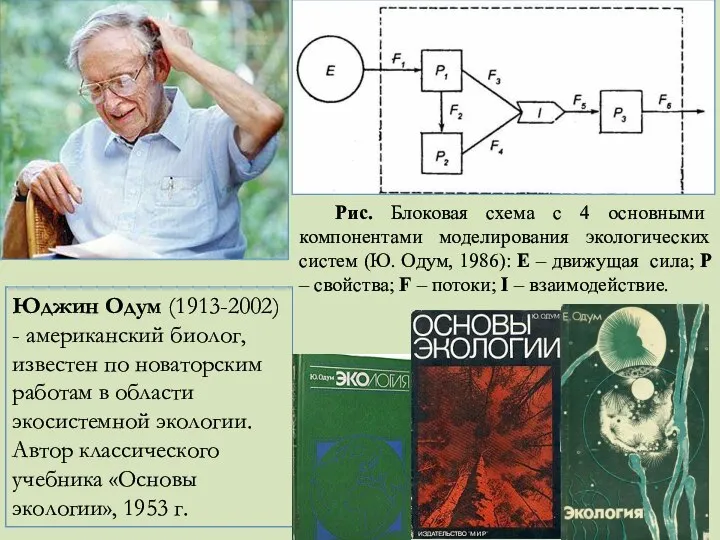
Блоковая схема с 4 основными компонентами моделирования экологических систем (Ю. Одум, 1986):
Е – движущая сила;
Р – свойства;
F – потоки;
I – взаимодействие.

Юджин Одум (1913-2002) - американский биолог, известен по новаторским работам в области экосистемной экологии. Автор классического учебника «Основы экологии», 1953 г.
Рис. Блоковая схема с 4 основными компонентами моделирования экологических систем (Ю. Одум, 1986): Е – движущая сила; Р – свойства; F – потоки; I – взаимодействие.

На рис. Р1 и Р2 - свойства, которые при взаимодействии (I) дают некое третье свойство Р3 (или влияют на него), когда система получает энергию от источника Е. Обозначены также пять направлений потоков вещества и энергии (F): F1 – вход, a F6 – выход для системы как целого. В модели экологической ситуации минимум четыре компонента:
1. источник энергии или другая внешняя движущая сила;
2. переменные состояний;
3. направления потоков, связывающих свойства между собой и с действующими силами через потоки энергии и вещества;
4. взаимодействия или функции взаимодействий между силами и свойствами, изменяя, усиливая или контролируя перемещение веществ и энергии или создавая качественно новые (эмерджентные) свойства.

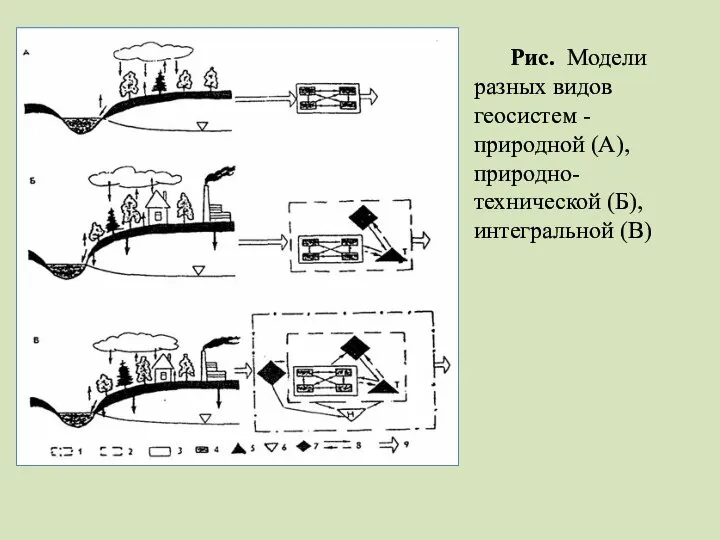
Рис. Модели разных видов геосистем - природной (А), природно-технической (Б), интегральной (В)

Блок-схема на рис. – модель лугопастбищной экосистемы: Р1 – зеленые растения, превращающие солнечную энергию Е в пищу. Р2 – растительноядное животное, поедающее растения, а Р3 – всеядное животное, которое может питаться как растительноядными, так и растениями.
Взаимодействие I - «случайный» переключатель, если наблюдения в реальном мире показали, что всеядное животное Р3 питается Р1 и Р2 без разбора в зависимости от их доступности. I имеет постоянное % значение при обнаружении, что рацион Р2 состоит, к примеру, на 80% из растительной и на 20% из животной пищи, независимо от того, каковы запасы P1 и Р2. I - «сезонный» переключатель, когда Р3 питается растениями в один сезон года и животными – в другой. Наконец, I – пороговый переключатель, если Р3 сильно предпочитает животную пищу и переключается на растения только тогда, когда уровень Р2 падает ниже определенного порога.

В качестве научной основы природопользования используется модель геосистемы (географической системы). Эта модель применяется в природопользовании для прогнозирования, а также с целью управления природопользованием посредством воздействия на один компонент для получения положительного эффекта от другого.
Природная геосистема – сравнительно простая географическая модель, саморегулирующаяся система. Ее целостность поддерживается взаимосвязью природных компонентов.
В более сложные модели в качестве нового элемента вводится человек (общество).

Схематические рисунки и соответствующие им графические модели справа показывают увеличение числа элементов, слагающих каждую геосистему, и связей между ними:
1 – граница интегральной геосистемы;
2 – граница природно-технической геосистемы;
3 – граница природной геосистемы;
4 – природные компоненты, элементы;
5 – технические элементы, подсистемы;
6 – население;
7 – орган управления, принимающий и контролирующий решения;
8 – связи между компонентами, элементами, подсистемами;
9 – связи на входе и выходе систем.

Суть метода: с помощью математических символов строится абстрактное упрощенное подобие изучаемой системы. Меняя значение отдельных параметров, исследуют, как поведет себя данная искусственная система, т.е. как изменится конечный результат.
Модели строят на основании сведений, накопленных в полевых наблюдениях и экспериментах. Чтобы построить адекватную математическую модель, требуются существенные эмпирические знания. Отразить все бесконечное множество связей популяции или биоценоза в единой математической схеме нереально. Однако, в надорганизменных системах имеется внутренняя структура и действует принцип «не все связи существенны», можно выделить главные связи и получить более или менее верное приближение к действительности.

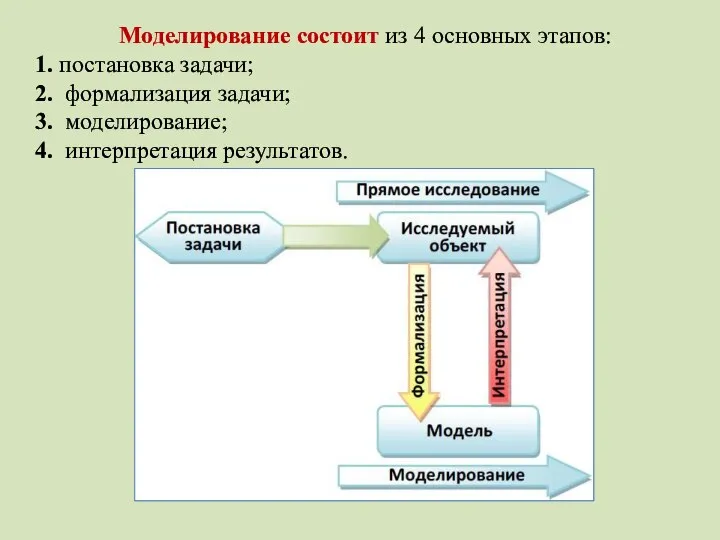
Моделирование состоит из 4 основных этапов:
1. постановка задачи;
2. формализация задачи;
3. моделирование;
4. интерпретация результатов.

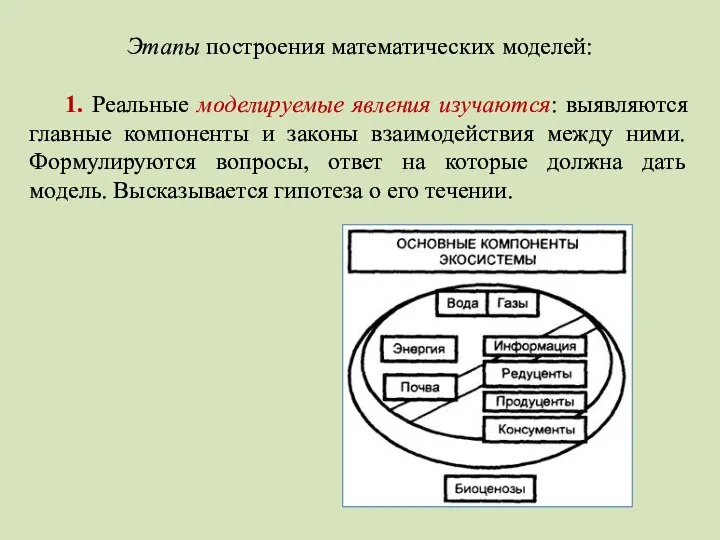
Этапы построения математических моделей:
1. Реальные моделируемые явления изучаются: выявляются главные компоненты и законы взаимодействия между ними. Формулируются вопросы, ответ на которые должна дать модель. Высказывается гипотеза о его течении.

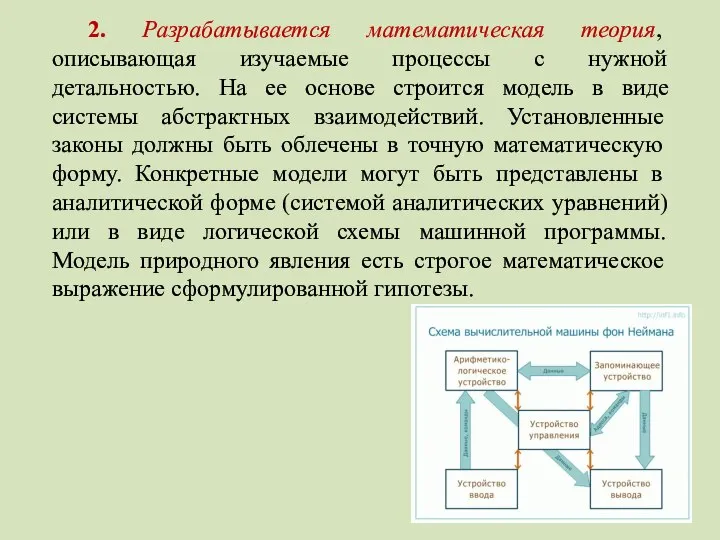
2. Разрабатывается математическая теория, описывающая изучаемые процессы с нужной детальностью. На ее основе строится модель в виде системы абстрактных взаимодействий. Установленные законы должны быть облечены в точную математическую форму. Конкретные модели могут быть представлены в аналитической форме (системой аналитических уравнений) или в виде логической схемы машинной программы. Модель природного явления есть строгое математическое выражение сформулированной гипотезы.

3. Проверка модели – расчет на основе модели и сличение результатов с действительностью. Проверяется правильность сформулированной гипотезы. При расхождении сведений модель отвергают или совершенствуют. При согласованности результатов модели используют для прогноза, вводя в них различные исходные параметры.
Математическая модель не абсолютное доказательство правильности гипотезы, так как может оказаться, что разные гипотезы приводят к сходным результатам, но она служит одним из путей анализа реальности.

В случае правильно построенной модели можно увидеть то, что трудно или невозможно проверить в эксперименте, воспроизводит процессы, наблюдение которых в природе потребовало бы много сил и времени. В математических моделях можно «проигрывать» разные варианты – вычленять разные связи, комбинировать отдельные факторы, упрощать или усложнять структуру систем, менять последовательность и силу воздействий - все это дает возможность лучше понять механизмы, действующие в природе.

Моделируют отдельные типы экологических взаимодействий хищник-жертва, паразит-хозяин, конкурентные отношения, мутуализм и др.
Математическими моделями описываются и проверяются варианты динамики численности популяций, продукционные процессы в экосистемах, условия стабилизации сообществ, ход восстановления систем при разных формах нарушений и многие др. явления.
Например, одну из простейших математических моделей для системы паразит-хозяин в динамике численности насекомых разработал в 1925 г. А. Лотка, который вывел следующие уравнения:

Альфред Джеймс Лотка (1880-1949) - амер. математик, физико-химик статистик, деморгаф. Известен за работу в области динамики популяций.

N1 – численность популяции хозяина; N2 – численность популяции паразита; r – удельная скорость увеличения популяции хозяина; d2 – удельная скорость гибели популяции паразита; р1, р2 – константы.
График процесса паразитической инвазии, построенный по таким уравнениям, обнаруживает, что в результате взаимодействия двух видов должны возникать осцилляции (колебания) с постоянной амплитудой, которая зависит от соотношения между скоростями увеличения численности двух видов.

В то же время математик В. Вольтерра выявил сходные закономерности для системы хищник-жертва, обрабатывая статистические данные рыбного промысла. Один из выведенных им законов - «закон периодического цикла»: процесс уничтожения одного вида другим может привести к периодическим колебаниям численности популяций обоих видов, зависящих только от коэффициентов роста популяций хищника и жертвы и от исходной относительной численности.
Ви́то Вольте́рра (1860-1940) — итальянский математик и физик.

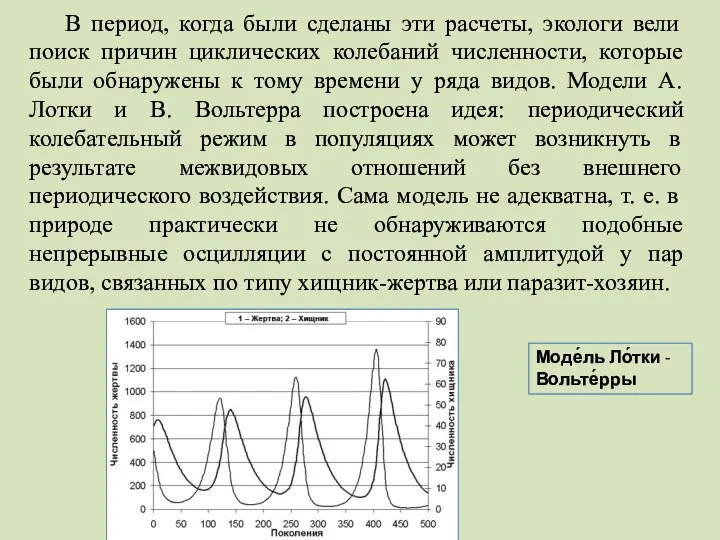
В период, когда были сделаны эти расчеты, экологи вели поиск причин циклических колебаний численности, которые были обнаружены к тому времени у ряда видов. Модели А. Лотки и В. Вольтерра построена идея: периодический колебательный режим в популяциях может возникнуть в результате межвидовых отношений без внешнего периодического воздействия. Сама модель не адекватна, т. е. в природе практически не обнаруживаются подобные непрерывные осцилляции с постоянной амплитудой у пар видов, связанных по типу хищник-жертва или паразит-хозяин.
Моде́ль Ло́тки - Вольте́рры

Уравнения А. Лотки и В. Вольтерра были чрезвычайно упрощенными, так как исходили из целого ряда допущений: что изменение численности популяции одного вида немедленно вызывает ответную реакцию популяции другого вида, что «аппетиты» хищника беспредельны, поиски жертв случайны, что плодовитость хищников пропорциональна численности всей популяции жертв.
В условиях упрощенного эксперимента с простейшими трудно добиться соблюдения этих допущений (Г. Ф. Гаузе,1934, 1935 гг.). В опытах с инфузориями удалось получить лишь два цикла хищник-жертва, после чего система пришла к разрушению. Во взаимодействиях хищника и жертвы распространен эффект «запаздывания» из-за разницы в скоростях размножения: степень насыщения («функциональная реакция») хищников, время, затрачиваемое ими на поиск и поимку добычи, способность переключаться на другую пищу, защитные приспособления жертв, размещение их в пространстве и территориальное поведение, возрастная и половая структура популяций и многое другое. Рост численности популяций может сдерживаться и другими причинами, в том числе внутривидовыми взаимоотношениями.

В 1933 г. А. Никольсон усложнил математическую модель Лотки, введя в систему дополнительных хозяев и паразитов, и показал, что это ослабляет осцилляции. В 1936 г. A. Колмогоров описал возможности устойчивого стационарного состояния системы взаимодействующих через трофические связи видов. С введением в модели дополнительных параметров сильно усложняется математический аппарат и техника расчетов. Многие из этих ограничений позволило снять использование ЭВМ.
Андрей Николаевич Колмого́ров (1903-1987) – русский советский математик, один из крупнейших математиков ХХ в. Один из основоположников современной теории вероятностей.

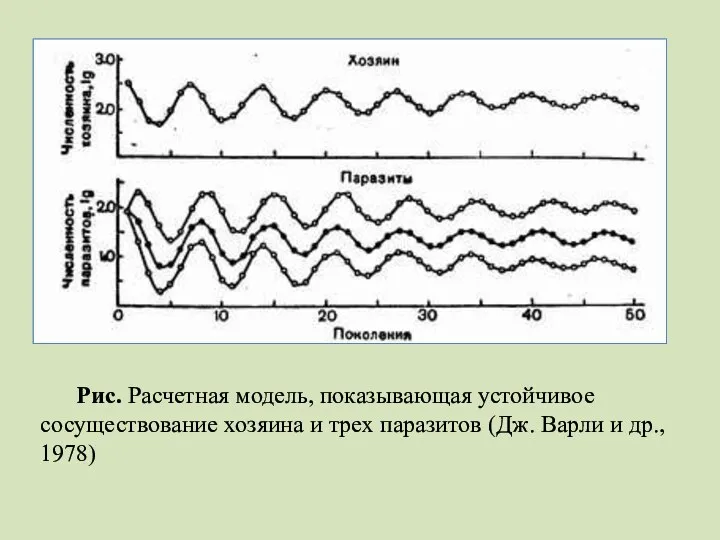
Рис. Расчетная модель, показывающая устойчивое сосуществование хозяина и трех паразитов (Дж. Варли и др., 1978)

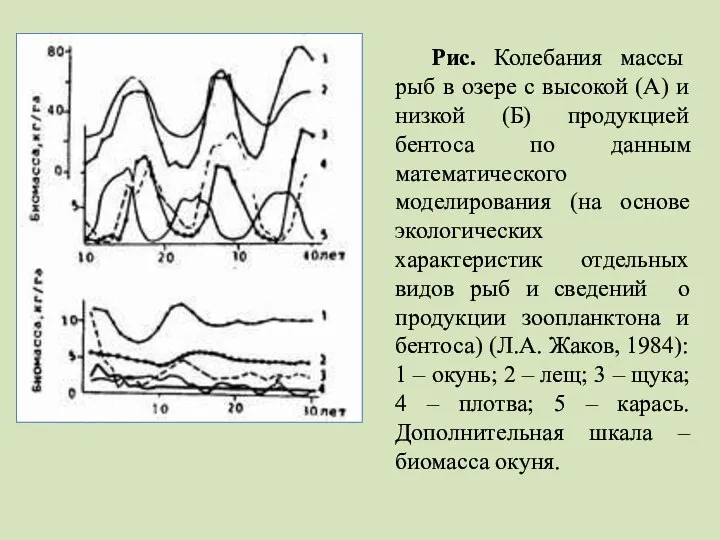
Рис. Колебания массы рыб в озере с высокой (А) и низкой (Б) продукцией бентоса по данным математического моделирования (на основе экологических характеристик отдельных видов рыб и сведений о продукции зоопланктона и бентоса) (Л.А. Жаков, 1984): 1 – окунь; 2 – лещ; 3 – щука; 4 – плотва; 5 – карась. Дополнительная шкала – биомасса окуня.

Модели хищник-жертва играют большую роль в планировании рыбного, китобойного, охотничьего промыслов, так как изъятие человеком части популяции диких животных с экологических позиций является аналогом природного хищничества.
Предельная степень эксплуатации, которую может выдержать популяция, различна у разных видов. Важно вовремя заметить симптомы, что изъятие из популяции приближается к предельно допустимому уровню, после которого нарушается ее воспроизводительная способность.

По результатам машинных экспериментов со статистикой китобойного промысла в 60-х годах выявлены показатели допустимых масштабов добычи и симптомы гибельной эксплуатации популяции синих китов.
Если популяция эксплуатируется интенсивно, но не чрезмерно, то в моделях обнаруживается уменьшение размеров и среднего возраста особей, кривые выживания изменяются, но не настолько, чтобы нарушалась плодовитость стада в целом. В реальной действительности были обнаружены предсказанные моделями симптомы гибельной эксплуатации китового стада – сокращение доли беременных самок, сильные изменения кривых выживания, уменьшение размеров уловов на единицу промыслового усилия, неспособность популяции быстро восстановить численность после прекращения промысла.
Синих китов осталось так мало, что несмотря на международный запрет их добычи 1967 г., поголовье остается на низком уровне и животные внесены в Красную книгу.

Моделирование трофических связей имеет большое значение для решения проблем борьбы с вредителями, регуляции численности популяций, стабилизации сообществ.
Математическое моделирование применяется при решении экологических проблем, связанных с антропогенными воздействиями на природную среду.
Тактические модели экосистем и популяций служат для экологического прогнозирования их состояния, в том числе при разного рода экзогенных воздействиях.
Стратегические модели строят с исследовательскими целями, для вскрытия общих законов функционирования биологических систем: стабильность, разнообразие, устойчивость к воздействиям, способность возвращаться в исходное состояние. В задачи стратегических моделей входит изучить с помощью ЭВМ последствия разных стратегий управления экосистемами, чтобы выбрать оптимальную.

Эколого-экономические модели описывают взаимодействие общества и природы и в которых учитывают не только экологические, но и экономические, демографические и социальные показатели. Такие модели разрабатывают для долгосрочного прогнозирования экономического роста и общей оценки влияния человеческой деятельности на природную среду.

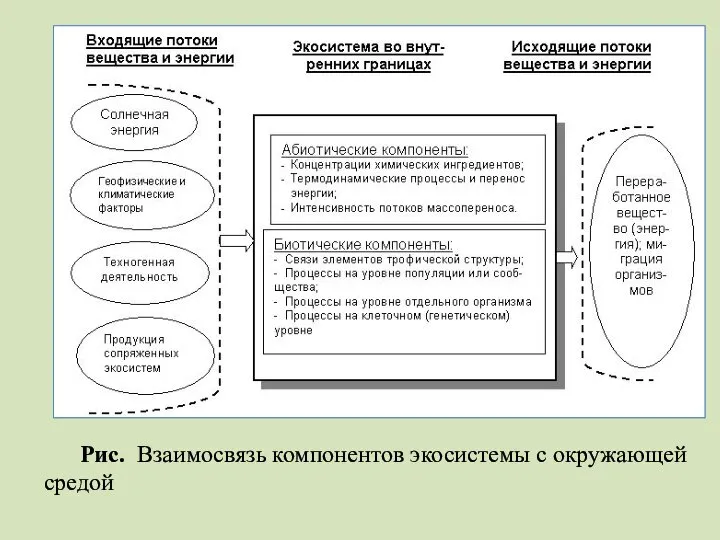
Рис. Взаимосвязь компонентов экосистемы с окружающей средой

Композиционные свойства систем определяются способом объединения элементов в функциональные группы и соотношением этих групп.
Группы элементов и подсистем:
эффекторные – способные преобразовывать воздействия и воздействовать веществом и энергией на другие подсистемы (например, техногенные компоненты экосистем);
рецепторные – способные преобразовывать внешние воздействия в информационные сигналы, передавать и переносить информацию (биоиндикаторные компоненты);
рефлексивные – способные воспроизводить внутри себя процессы на информационном уровне (измеряющие компоненты).

Основные принципы системологии (Флейшман и др., 1982; Розенберг, 1984; Розенберг с соавт., 1999):
принцип эмерджентности (Реймерс, 1990), по Ю. Одум (1986): ... «принцип не сводимости свойств целого к сумме свойств его частей должен служить первой рабочей заповедью экологов»;
принцип иерархической организации (принцип интегративных уровней; Одум, 1975);
принцип несовместимости Л. Заде (1974): чем глубже анализируется реальная сложная система, тем менее определенны наши суждения о ее поведении;
принцип контринтуитивного поведения Дж. Форрестера (1977, 1978): дать удовлетворительный прогноз поведения сложной системы на достаточно большом промежутке времени, опираясь только на собственный опыт и интуицию, практически невозможно.

Наиболее часто используются иерархические классификации [Айвазян с соавт., 1974; Жамбю, 1988], которые могут быть представлены в двух основных формах – дерева (фиг. А рис. 2.3) и вложенного множества (фиг. В). Дерево представляет собой специальный вид направленного графа – структуры, состоящей из узлов, связанных дугами. Дерево иерархической классификации обладает следующими свойствами:
имеется один и только один корень (иногда в полном противоречии с ботаникой его называют вершиной);
всегда имеется путь от корня до любого другого узла в дереве;
каждый узел, кроме корня, имеет одного и только одного родителя (т.е. граф не должен иметь циклов и петлей) и произвольное число потомков;
узлы дерева, которые не имеют потомков, называются листьями и они соответствуют исходному множеству классифицируемых объектов.
Рис. Методы представления результатов классификации (А – дерево, В – вложенное множество)

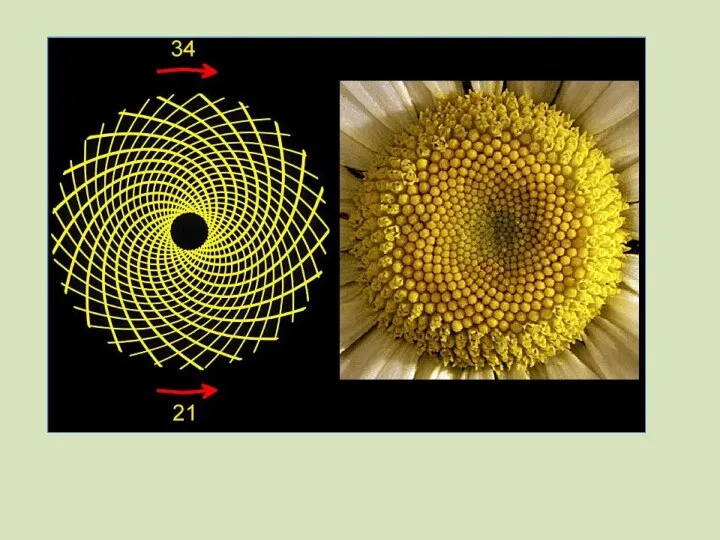
Числа Фибоначчи, названные в честь Леонарда Пизанского – итальянского математика, познакомившего Европу с десятичной системой исчисления. Он вывел последовательность, при которой каждое следующее число составляет сумму двух предыдущих чисел: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34……. и так до бесконечности. Эта последовательность есть в пчелиных сотах, сосновой шишке, узоре семян подсолнуха, расположении листьев на ветке (филотаксис). Если вы решите пересчитать спирали зерен подсолнуха, которые располагаются по и против часовой стрелки от центра до внешнего края, то обнаружите пару чисел из данной последовательности: скажем, 34 и 55 или 55 и 89, а если повезет и вы встретите очень крупный подсолнух, то возможно – 89 и 144. В Музее науки и промышленности Манчестера посредством краудсорсинга уже 4 года представители общественности занимаются выращиванием своих собственных подсолнухов и передают в музей их фотографии вместе с отчетами о спиральных узорах, проанализировано 657 цветков. В 4 случаях из 5 пары семейств парастих (рядов) демонстрируют числа из ряда Фибоначчи, а остальных случаях – из схожих последовательностей (ряд Люка 1, 3, 4, 7, 11 и т. д.) или даже более сложных моделей.

Продолжим тему математики в ботанике. Это так интересно! Многочисленные и очень далекие по родству представители флоры дружно являют приверженность ряду чисел Фибоначчи, где каждый последующий член равен сумме двух предыдущих: 1 1 2 3 5 8 13 21 34 …Начиная с Гофмейстера (1868) и Эйри (1873), рассматривают расположение не столько листьев, сколько их зачатков в верхушке почки – примордиях. Филлотаксис (листорасположение) – порядок размещения листьев на оси побега. Закономерности размещения листьев связаны с деятельностью апекса побега и отражают его радиальную симметрию. Чаще всего в природе встречается спиральное, или очередное, листорасположение с одним примордием на узле: береза, традесканция, ананас. Верхушки некоторых побегов не удлиняются при появлении новых примордиев, а раздаются в ширину, уплощаются, и получаются подсолнухи, ромашки. Рядом стоящие повторяющиеся элементы паттернов формируют ряды – парастихи. Примордии в парастихе могут быть в контакте, тогда парастиха хорошо различима и заметна. Такие парастихи называются контактными. http://filov.mypage.ru

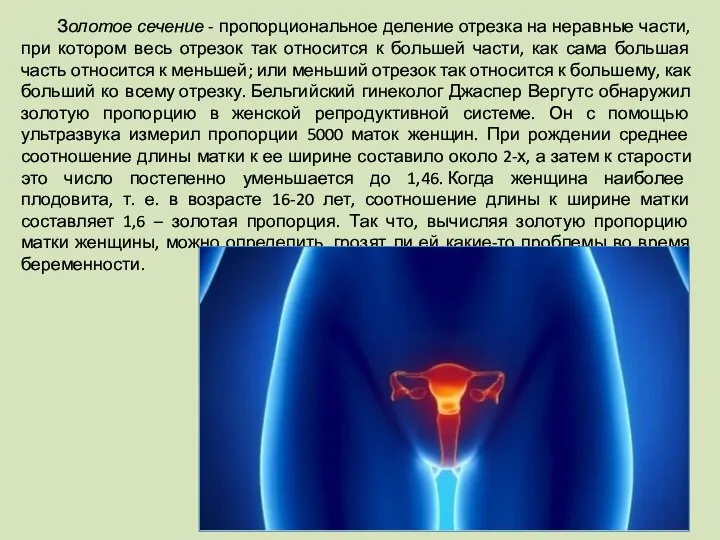
Золотое сечение - пропорциональное деление отрезка на неравные части, при котором весь отрезок так относится к большей части, как сама большая часть относится к меньшей; или меньший отрезок так относится к большему, как больший ко всему отрезку. Бельгийский гинеколог Джаспер Вергутс обнаружил золотую пропорцию в женской репродуктивной системе. Он с помощью ультразвука измерил пропорции 5000 маток женщин. При рождении среднее соотношение длины матки к ее ширине составило около 2-х, а затем к старости это число постепенно уменьшается до 1,46. Когда женщина наиболее плодовита, т. е. в возрасте 16-20 лет, соотношение длины к ширине матки составляет 1,6 – золотая пропорция. Так что, вычисляя золотую пропорцию матки женщины, можно определить, грозят ли ей какие-то проблемы во время беременности.

Странную, загадочную, божественную пропорцию мы увидим и в изгибах морских раковин, и форме цветов, и облике жуков, и красивом человеческом теле. В основе золотой спирали лежит золотое сечение - коэффициенты Фибоначчи. Золотая логарифмическая спираль - даже в основе спиральных галактик.

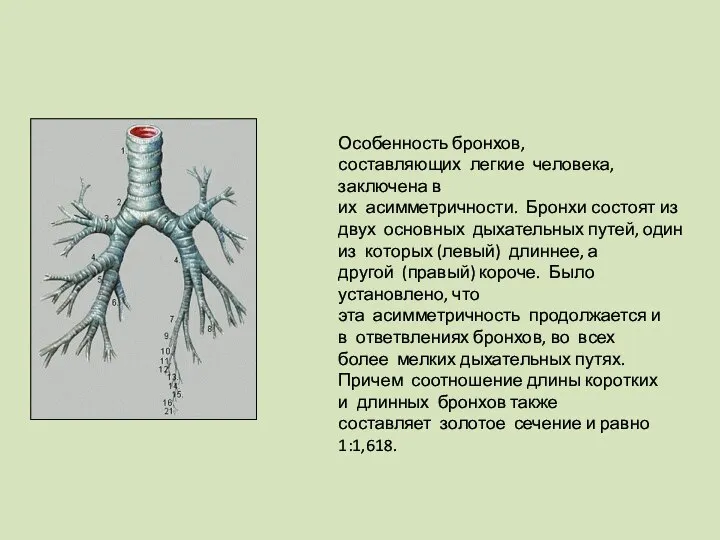
Особенность бронхов, составляющих легкие человека, заключена в их асимметричности. Бронхи состоят из двух основных дыхательных путей, один из которых (левый) длиннее, а другой (правый) короче. Было установлено, что эта асимметричность продолжается и в ответвлениях бронхов, во всех более мелких дыхательных путях. Причем соотношение длины коротких и длинных бронхов также составляет золотое сечение и равно 1:1,618.

Давление крови изменяется в процессе работы сердца. Наибольшей величины оно достигает в левом желудочке сердца в момент его сжатия (систолы). В артериях во время систолы желудочков сердца кровяное давление достигает максимальной величины, равной 115-125 мм рт. ст. у молодого, здорового человека. В момент расслабления сердечной мышцы (диастола) давление уменьшается до 70-80 мм рт.ст. Отношение максимального (систолического) к минимальному (диастолическому) давлению равно в среднем 1,6, то есть близко к золотой пропорции.

Земле все должны. День экологического долга (Overshoot Day) – точка в каждом календарном году, когда потребление природных ресурсов превышает способность территории или Земли восполнять потребление этих ресурсов в текущем году. Например, в Финляндии потребление природных ресурсов значительно выше среднего по планете. Если бы все население Земли потребляло природные ресурсы так же, как жители этой небольшой, процветающей страны, нам понадобилось бы иметь 3,6 планеты Земля для поддержания устойчивого образа жизни. В этой стране большое количество природных ресурсов потребляется в энергетике, на транспорте и в производстве продуктов питания. В глобальном масштабе День экологического долга Земли в этом году ожидается в начале августа. Методика расчета этой даты признается не всеми экологическими организациями и вызывает немало споров.

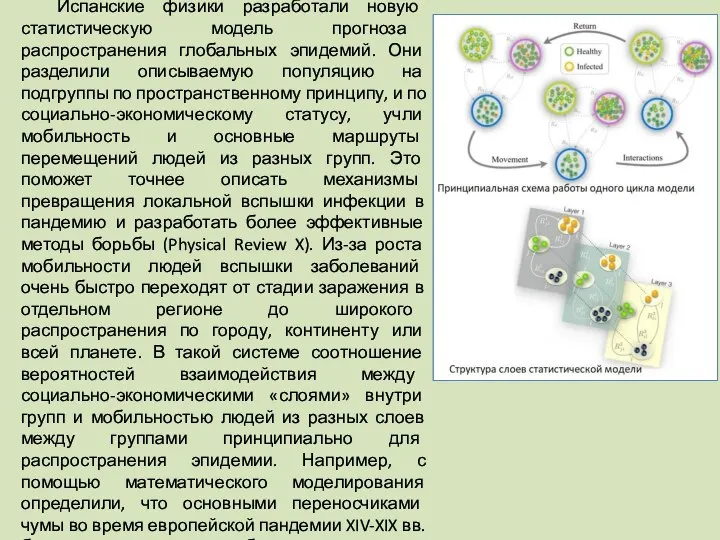
Испанские физики разработали новую статистическую модель прогноза распространения глобальных эпидемий. Они разделили описываемую популяцию на подгруппы по пространственному принципу, и по социально-экономическому статусу, учли мобильность и основные маршруты перемещений людей из разных групп. Это поможет точнее описать механизмы превращения локальной вспышки инфекции в пандемию и разработать более эффективные методы борьбы (Physical Review X). Из-за роста мобильности людей вспышки заболеваний очень быстро переходят от стадии заражения в отдельном регионе до широкого распространения по городу, континенту или всей планете. В такой системе соотношение вероятностей взаимодействия между социально-экономическими «слоями» внутри групп и мобильностью людей из разных слоев между группами принципиально для распространения эпидемии. Например, с помощью математического моделирования определили, что основными переносчиками чумы во время европейской пандемии XIV-XIX вв. были человеческие вши и блохи, а не паразиты грызунов.

Матмоделирование в действии, но не в реальности. Ученые университета Монаша в Мельбурне построили матмодель, по которой можно узнать, сколько человек погибнет из-за аномальной жары в 2031-2080 гг. По подсчетам климатологов средняя температура на планете будет расти. В расчет взяты изменения климата при различных сценариях, адаптация к ним и изменение количества населения. Использована информация о погоде и смертности 400 районов в 20 странах, собранная в Северной и Южной Америках, Европе и Азии (кроме России) в период с 1984 по 2015 гг. По расчетам волны жары станут более интенсивными, частыми и продолжительными. Летальность по причине перегрева вырастет на 770 % относительно средних уровней до 2020 г. Первыми под удар попадут Филиппины, Бразилия, Колумбия и др. страны экваториального пояса. В южных районах США прирост смертности может составить 400-525%, а в Европе не превысит 400 %. Аналогичные цифры получены для Китая и Японии.

От информатики к морфогенезу. Описаны характеристики узора из чешуек на теле акул по теории британского математика Алана Тьюринга, выдвинутой более 60 лет назад. Алан Тьюринг один из основоположников информатики и теории вычислительных машин. В конце жизни он интересовался биологией, и в 1952 г. в статье «Химические основы морфогенеза» описал при помощи системы уравнений возникновение полос, пятен и спиральных узоров в живой материи. С помощью идеи Тьюринга правильно воспроизведено расположение волосков шерсти мышей и перьев кур (журнал Science Advances). Акулы давно отделились от других челюстных, поэтому исследование их развития позволяет лучше понять, как могла выглядеть кожа ранних позвоночных. Возможно, эта работа позволит создать покрытия подводных костюмов и аппаратов, которые уменьшают сопротивление воды.

Килограмма больше нет? 130 лет платиново-иридиевый цилиндр в вакуумированном колоколе Международного бюро мер и весов во французском Севре служил эталоном килограмма. Каждые 40 лет его вывозили для калибровки подобных эталонов по всему миру. В Версальском дворце 13-16 ноября 2018 года 26-я Генеральная конференция мер и весов лишила нас физических эталонов системы СИ. Эталоны килограмма, ампера, кельвина и моля будут определены напрямую через физические фундаментальные константы, как уже это сделано для секунды, метра и канделы. Первые эталоны метра и килограмма были созданы в Париже в 1799 г. Но международная Метрическая конвенция подписана 17 государствами, в том числе и Россией, только в 1878 г. Тогда же появился Международный комитет мер и весов – организация по международным эталонам. Ясно, что любой физический эталон – это условность, так как он изменяется из-за испарения, диффузии, температуры и др. Поэтому начали выражать единицы системы СИ через фундаментальные физические константы. В практическом смысле мало что изменится, эталоны для калибровки весов останутся. Однако метрологи начнут разрабатывать максимально точно поверенные весы Киббла - устройства, при помощи которых определяется постоянная Планка (м2кг/с). Каждое измерение постоянной определит величину килограмма.

Осторожно, сейчас ты станешь слишком умным или куска аптеки пост! Двойной слепой рандомизированный плацебо-контролируемый метод – способ клинического исследования лекарств, при котором испытуемых не посвящают в важные детали проводимого исследования. «Двойной слепой» означает, кого чем лечат, не знают ни испытуемые, ни экспериментаторы, «рандомизированный» - распределение по группам случайно, а плацебо для того, чтобы показать, что действие препарата не самовнушение и данное лекарство помогает лучше, чем таблетка без действующего вещества. Этот метод против субъективного искажения результатов. Иногда группе контроля дают другой препарат с уже доказанной эффективностью, а не плацебо, чтобы показать, что препарат не просто лечит лучше, чем ничего, но и превосходит аналоги. Могла бы спросить: хотели бы поучаствовать в подобных испытаниях ради науки? Но не буду спрашивать о таком.

Куда уводят мечты и идеи? Географический детерминизм – концепция об общественном развитии под влиянием природных сил. Устройство поверхности, климат, почва, растительность, животный мир – естественные факторы, которые определяют общественный строй, хозяйственное развитие стран, и даже физические и психические черты людей: способности, наклонности, темперамент. География – это физиология и сравнительная анатомия Земли: реки, горы, ледники – органы с собственными функциями. Физическая география – основа развития общества и определяет ход жизни общества и человека. Все хорошо, но что-то пошло не так: к географическому детерминизму примыкает расовая антропология, и социал-дарвинизм Европы среди образованных людей ХХ века, восхищавшихся культом силы как фактором эволюции живой природы.