Лекция_Модель межотраслевого баланса Леонтьева

Историческая справка
Модель МОБ была предложена американским математиком Василием Леонтьевым в 1936 году, а в 1967 году Леонтьев был удостоен Нобелевской премии в области экономики.
Модель Леонтьева позволяет:
проводить исследования сложившихся пропорций,
определять горизонтальные связи,
составлять планы материально-технологического обеспечения,
определять информационные потоки, необходимые для разработки управленческих решений.

Структурный подход как один из способов анализа макроэкономических процессов
В зависимости от цели исследования экономику можно изучать как в структурированном виде, так и в форме единой, неделимой системы на различных уровнях - от уровня национальной экономики до уровня отдельных фирм и потребителей.
Целью построения модели Леонтьева является анализ перераспределения товаров между отраслями экономики, обеспечивающего такое функционирование производственного сектора, когда объем выпуска соответствует суммарному спросу на товары.
В этом случае экономика рассматривается в разукрупненном до уровня отраслей виде.

Межотраслевой баланс (МОБ) производства и распределения продукции – это инструмент анализа и планирования структуры общественного производства, учитывающий комплексные взаимосвязи отраслей производственной сферы.
Модели МОБ применяются для анализа и планирования на разных иерархических уровнях управления – от деятельности предприятия до функционирования народного хозяйства в целом.
В основе создания этих моделей лежит балансовый метод, т.е. метод взаимного сопоставления ресурсов и потребностей в них. Под балансовой моделью понимается система уравнений, каждое из которых выражает требование баланса между производимым количеством продукции и совокупной потребностью в этой продукции.

Виды балансов
В зависимости от цели и объекта исследования балансы классифицируют:
по единицам измерения – натуральные, натурально-стоимостные, стоимостные, трудовые;
по объектам анализа – народнохозяйственные, районные, внутриотраслевые межпродуктовые;
по периоду анализа – статические и динамические;
по цели исследования – отчетные, плановые.

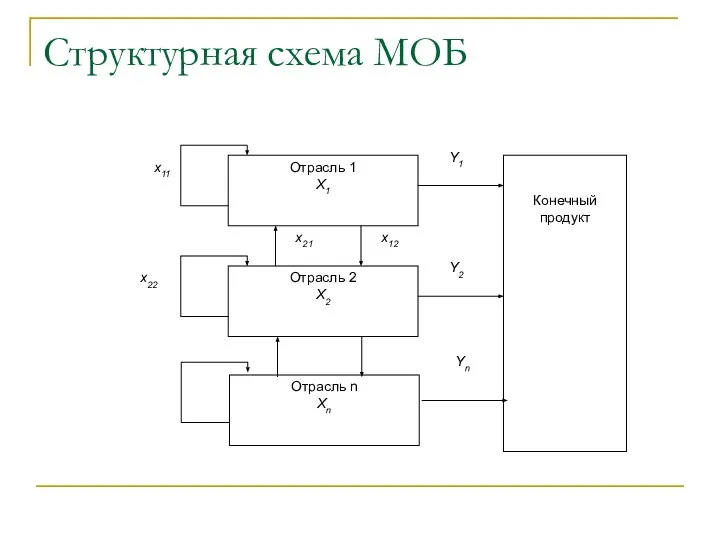
Структурная схема МОБ

Допущения модели
В основу схемы МОБ положены следующие предположения:
совокупный общественный продукт делится на две части: промежуточный и конечный продукт;
в экономической системе производятся и потребляются n- продуктов;
каждая отрасль является «чистой», то есть производит только один продукт, а различные отрасли производят разные продукты;
независимо от масштаба производства удельный выпуск и соотношение затрат предполагаются постоянными.

Обозначения
Xi – валовой продукт i-той отрасли;
Yi –конечная продукция i-той отрасли, т.е. продукция, которая выходит в область конечного использования (потребление + накопление);
xij – величины межотраслевых потоков, где i – производящие отрасли, j – потребляющие отрасли;
Сj – сумма амортизации;
Vj – оплата труда;
mj – чистый доход.
Сумму амортизации и чистой продукции будем называть условно чистой продукцией.
Zj = Cj + (Vj + mj) – условно чистая продукция.

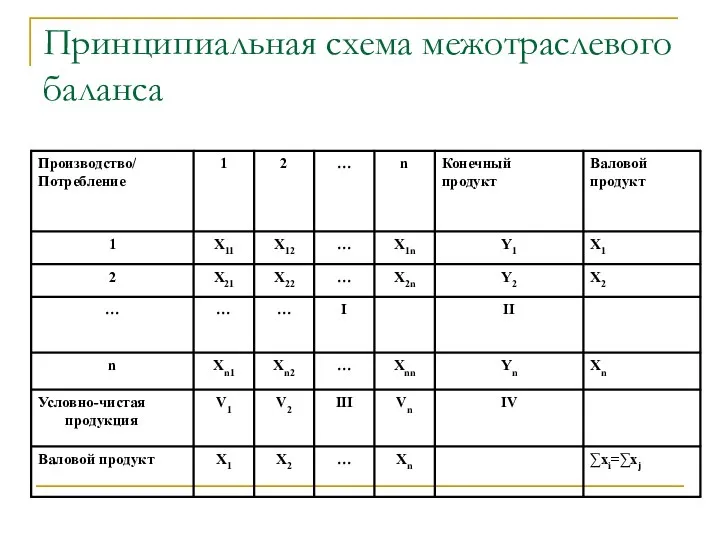
Принципиальная схема межотраслевого баланса

Схема МОБ представляет собой синтез двух таблиц, одна из которых характеризует детальную структуру затрат на производство в разрезе отдельных видов продукции, а другая – структуру распределения продукции в народном хозяйстве

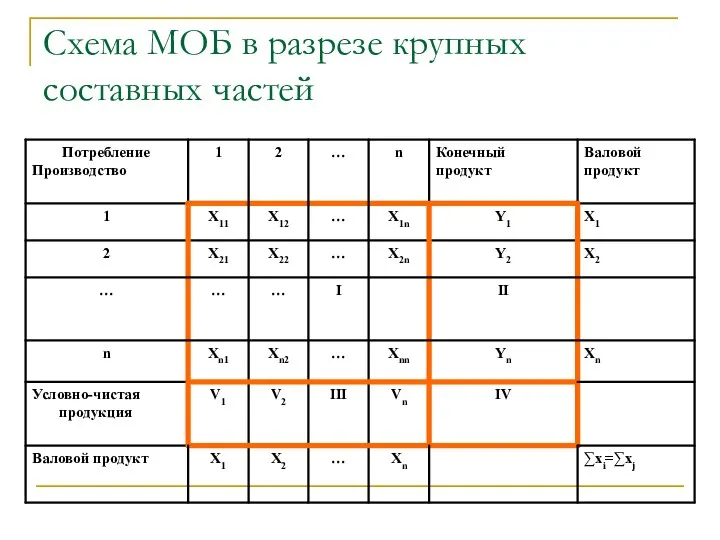
Схема МОБ в разрезе крупных составных частей

Характеристика квадрантов баланса
I квадрант МОБ – шахматная таблица межотраслевых материальных связей. По форме он представляет собой квадратную матрицу порядка n, сумма всех элементов которой равняется годовому фонду возмещения затрат средств производства в материальной сфере;
II квадрант характеризует отраслевую материальную структуру национального дохода;
III квадрант характеризует структуру национального дохода, но со стороны его стоимостного состава;
IV квадрант баланса находится на пересечении столбцов II квадранта и строк III квадранта. Он отражает конечное распределение и использование национального дохода. Данные IV квадранта важны для отражения в МОБ баланса доходов и расходов населения, источников финансирования капиталовложений, текущих затрат непроизводственной сферы, для анализа общей структуры конечных доходов по группам потребителей.

Валовая продукция отраслей представлена на принципиальной схеме МОБ в двух местах в виде столбца, расположенного справа от второго квадранта и в виде строки ниже третьего. Эти столбец и строка валовой продукции замыкают схему МОБ и играют важную роль как для проверки правильности заполнения квадрантов, так и для разработки экономико-математической модели межотраслевого баланса.

Построение модели: 1 шаг
Рассмотрим схему баланса по столбцам:
(1)
система из n уравнений, отражающих стоимостной состав продукции всех отраслей.

Шаг 2
Рассмотрим схему баланса по строкам:
(2)
система из n уравнений, которые называются уравнениями распределения продукции по направлениям использования.

Шаг 3
Просуммируем по всем отраслям уравнения (1):
Аналогично просуммируем (2):
Левые части обоих равенств равны, так как представляют собой валовой общественный продукт, первые слагаемые правых частей этих равенств также равны, следовательно должно выполняться соотношение:
(3)
(3) показывает, что в межотраслевом балансе соблюдается принцип единства материального и стоимостного состава национального дохода.

Основу информационного обеспечения модели МОБ составляет технологическая матрица, содержащая коэффициенты прямых материальных затрат на производство единицы продукции.
Определение 1.
Величины (4)
называются коэффициентами прямых материальных затрат.
С учетом (4) систему уравнений (2) можно записать
(5)

Уравнение Леонтьева
Обозначим А - матрицу коэффициентов прямых материальных затрат А=(aij);
-вектор-столбец валовой продукции;
-вектор-столбец конечной продукции.
Получим:

Система уравнений (5), или в матричном виде (6)- называется экономико-математической моделью межотраслевого баланса,
моделью Леонтьева, моделью «Затраты-выпуск».

Задачи, решаемые на основе модели
1. Задав в модели (6) величины валовой продукции Xi, можно определить объемы конечной продукции Yi:
(7)
2. Задав величины конечной продукции Yi,можно определить величины валовой продукции:
(8)
3. Для ряда отраслей задав величины валовой продукции Xi, а для всех остальных отраслей величины конечной продукции Yi, можно найти неизвестные величины Xi и Yi воспользовавшись не матричной формой модели, а системой линейных уравнений (5).

Элементы матрицы В будем обозначать через bij, тогда можно получить следующее соотношение:
Коэффициенты bij- называются коэффициентами полных материальных затрат и включают в себя как прямые, так и косвенные затраты всех порядков.
Определение 2.
Коэффициенты полных материальных затрат bij показывают, какое количество продукции i-ой отрасли нужно произвести, чтобы с учетом прямых и косвенных затрат этой продукции получить единицу конечной продукции j-ой отрасли.

Свойства матрицы А
1. Коэффициенты прямых материальных затрат не могут быть отрицательными, следовательно А >=0, то есть матрица А является неотрицательной.
2. Для собственного воспроизводства должно затрачиваться меньше продукта, нежели воспроизводится, следовательно диагональные элементы <1.
Содержательный смысл могут иметь лишь значения валовых выпусков Х>0, поэтому встает вопрос, при каких условиях экономическая система способна обеспечить положительный конечный выпуск по всем отраслям.
Определение 3. Неотрицательная матрица А называется продуктивной , если существует такой вектор Х>0, что
Х>А*Х (9)
То есть (9) обеспечивает существование положительного вектора конечной продукции Y>0.

Условия продуктивности
1. Матрица (Е-А)-неотрицательно обратима,
т. е. все элементы матрицы
B=(bij)>=0.
2. Все главные миноры матрицы (Е-А) положительны.
3. Наибольшее по модулю собственное значение матрицы А строго меньше 1.
Достаточным (но не необходимым) условием является условие

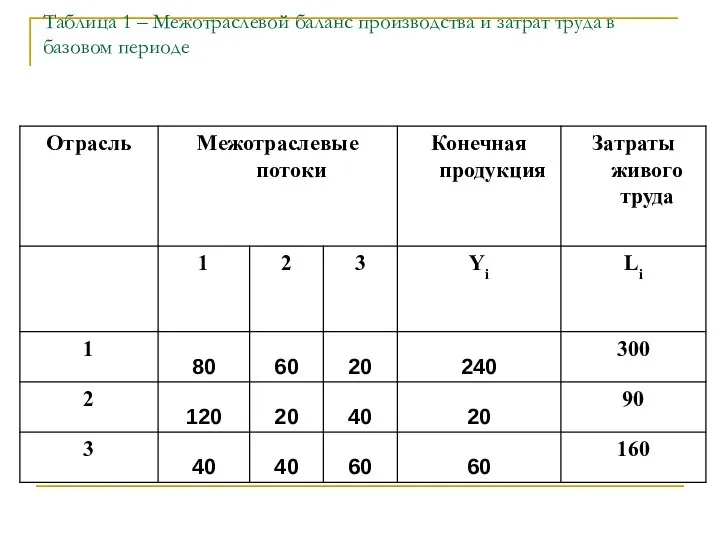
Пример практического задания
На основе матрицы межотраслевых потоков и вектора конечной продукции схемы межотраслевого баланса в базовом периоде (таблица 1) требуется:
построить матрицу коэффициентов прямых материальных затрат;
проверить продуктивность матрицы коэффициентов прямых материальных затрат;
рассчитать матрицу коэффициентов полных материальных затрат;
найти объемы валовой продукции отраслей для планового периода, если известен вектор конечной продукции в плановом периоде (таблица 2);
восстановить схему межотраслевого материального баланса в плановом периоде;
сделать вывод о возможности удовлетворения конечного спроса в плановом периоде и предложить варианты управленческих решений, если имеются ограничения, связанные с а) производственной мощностью отраслей; б) отраслевым распределением трудовых ресурсов.

Таблица 1 – Межотраслевой баланс производства и затрат труда в базовом периоде

Таблица 2 – Информация о конечной продукции и ограничения по ресурсам в плановом периоде

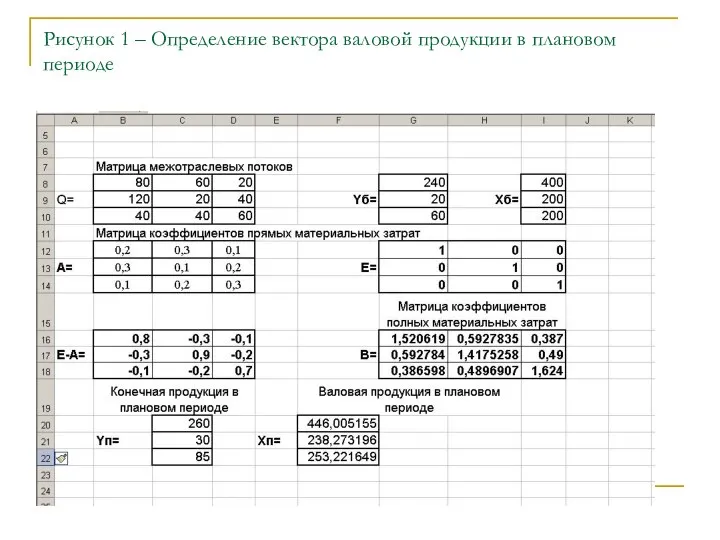
Рисунок 1 – Определение вектора валовой продукции в плановом периоде

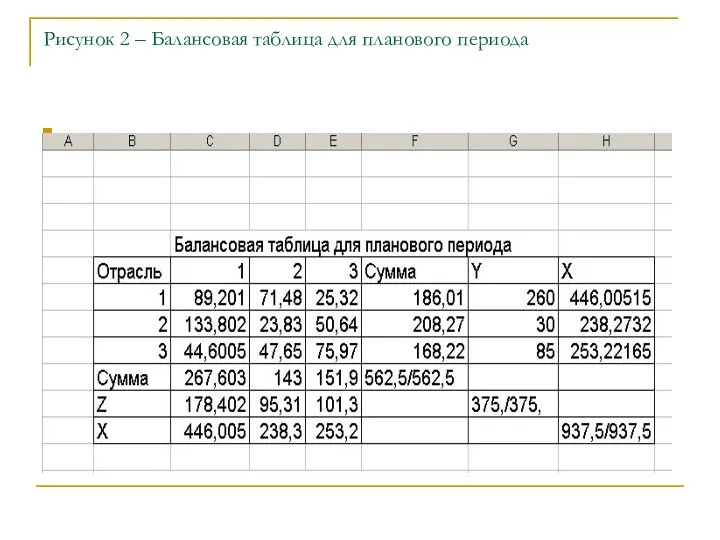
Рисунок 2 – Балансовая таблица для планового периода

Анализ возможности реализации плана
Сопоставляя планируемый валовой выпуск и имеющиеся производственные мощности можно сделать вывод о том, что выполнение плана по конечной продукции в целом невозможно ввиду недостаточной производственной мощности второй отрасли. В такой ситуации можно ставить вопрос не об удовлетворении любого вектора спроса. А только такого, на который достаточно мощностей. Если считать, что структура спроса задана, тогда при существующей технологии и ограниченности мощностей ставится задача максимизации конечного спроса в заданной структуре.

Математическая модель задачи
примет вид:
Таким образом, получили задачу линейного программирования, в которой (n+1) искомая переменная.

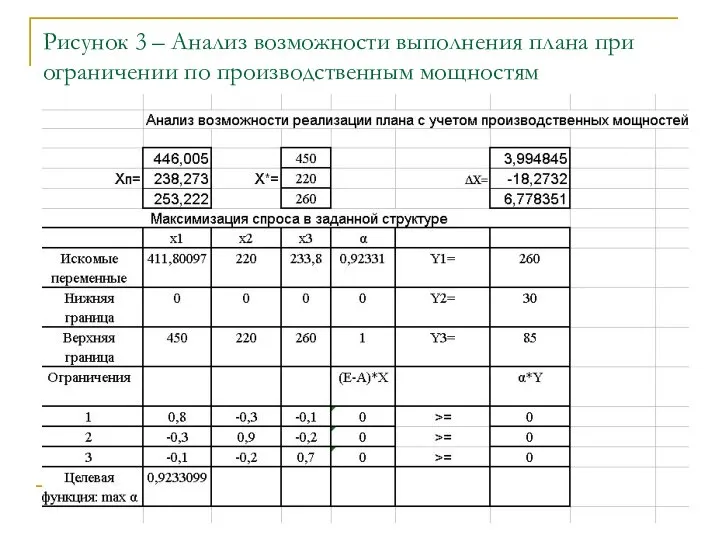
Рисунок 3 – Анализ возможности выполнения плана при ограничении по производственным мощностям

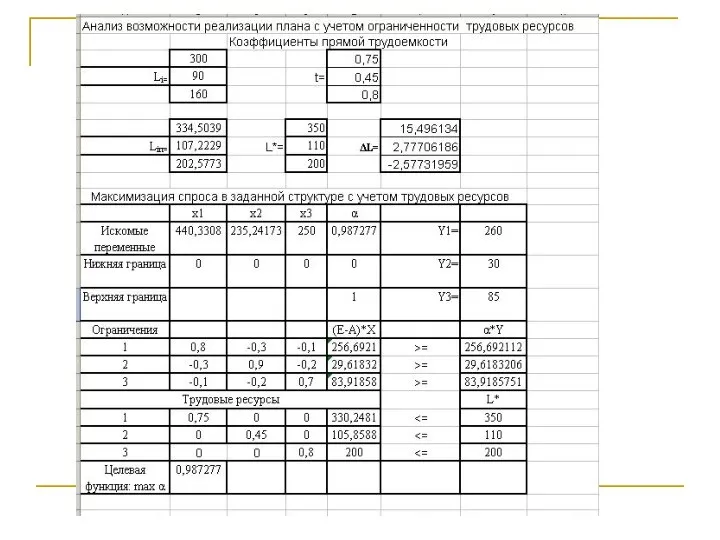
Анализ трудовых ресурсов
Проведем анализ обеспечения плановых показателей трудовыми ресурсами. Для этого определим коэффициенты прямой трудоемкости на основе информации базового периода по формуле:
Далее, зная валовую продукцию в плановом периоде можно определить потребности в трудовых ресурсах для каждой отрасли:
.

В случае невозможности достичь первоначальных плановых показателей вырабатываются рекомендации по возможным решениям в плановом периоде. Например, можно по аналогии с анализом производственной мощности, потребовать максимизации структуры конечного спроса путем решения задачи, математическая модель которой будет иметь вид:

Недостатки статической модели МОБ
Статическая модель МОБ обладает рядом недостатков, из-за которых ее трудно использовать для прогнозирования на длительный период. Например, в модели предполагаются независимыми объемы инвестиций и объемы выпуска. Кроме того, предполагаются постоянными коэффициенты затрат. Чтобы избежать несоответствия, были разработаны динамические модели планирования, которые отличаются тем, что учитывают предыдущее развитие экономики, а не только фиксируют состояние на данный период.
Динамическая модель в отличие от статической отражает обратную связь между инвестициями, с одной стороны, и объемом прироста валовой продукции, с другой. Схематически это выражается в появлении дополнительной таблицы, отражающей связь между инвестициями и приростом валовой продукции по отраслям.

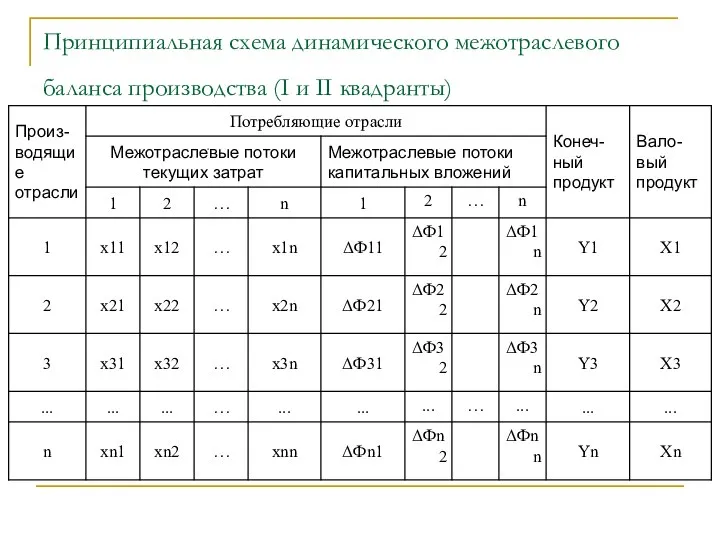
Принципиальная схема динамического межотраслевого баланса производства (I и II квадранты)

Различия
Модель содержит две матрицы межотраслевых потоков. Матрица текущих производственных затрат с элементами xij совпадает с соответствующей матрицей статического баланса. Элементы второй матрицы ΔФij показывают, какое количество продукции i-ой отрасли направлено в текущем периоде в j-ую отрасль в качестве производственных капитальных вложений в ее основные фонды. Материально это выражается в приросте в потребляющих отраслях производственного оборудования , сооружений, производственных площадей, транспортных средств.

В динамической схеме конечный продукт Yi включает продукцию i-ой отрасли, идущую в личное и общественное потребление, накопление непроизводственной сферы, прирост оборотных фондов. Таким образом, сумма потоков капиталовложений и конечного продукта динамической модели равна конечной продукции статического баланса:

Поэтому уравнение распределения продукции в динамическом балансе имеет вид:

Если текущий период обозначить через t, то прирост продукции ΔXj равен разности абсолютных уровней производства в период t и в предшествующий (t-1) –й период:
ΔXj=Xjt-Xj(t-1).
Полагая, что прирост продукции пропорционален приросту производственных фондов, можно записать:
ΔФij=ϕij*ΔXj, i,j=1,n.
Откуда ϕij =ΔФij /ΔXj.

Коэффициенты приростной фондоемкости
Экономический смысл этих коэффициентов заключается в том, что они показывают, какое количество продукции i-ой отрасли должно быть вложено в j-ую отрасль для увеличения производственной мощности j-ой отрасли на единицу продукции. Коэффициенты ϕij называются коэффициентами вложений или коэффициентами приростной фондоемкости.

С помощью введенных коэффициентов и если учесть, что все объемы валовой и конечной продукции относятся к некоторому периоду t, а прирост валовой продукции определен в соответствии с (t-1)-м периодом, можно записать следующие соотношения :

Переходя от дискретного анализа к непрерывному, для случая непрерывных изменений получим следующую систему соотношений:
Соотношения (5) представляют собой систему n линейных дифференциальных уравнений первого порядка с постоянными коэффициентами. Для ее решения помимо матриц коэффициентов прямых материальных затрат необходимо знать уровни валового выпуска в начальный момент времени t=0 и закон изменения величины конечного продукта т. е. вид функции Yi’. На основе этих данных путем решения получившейся задачи Коши для системы дифференциальных уравнений можно найти уровни валового выпуска теоретически для любого момента времени.