Содержание
- 2. Sinking into memories: A general production function in the Solow growth model Consider a general production
- 3. Sinking into memories: The Cobb-Douglas production function One simple production function that provides – as many
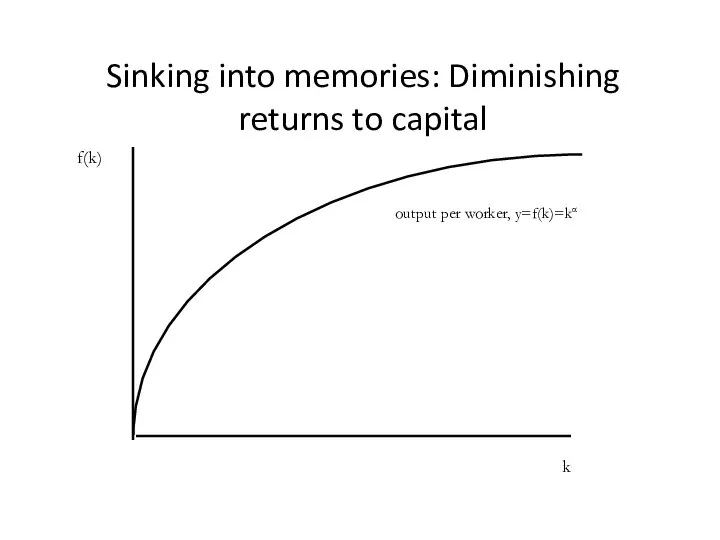
- 4. Sinking into memories: Diminishing returns to capital output per worker, y=f(k)=kα f(k) k
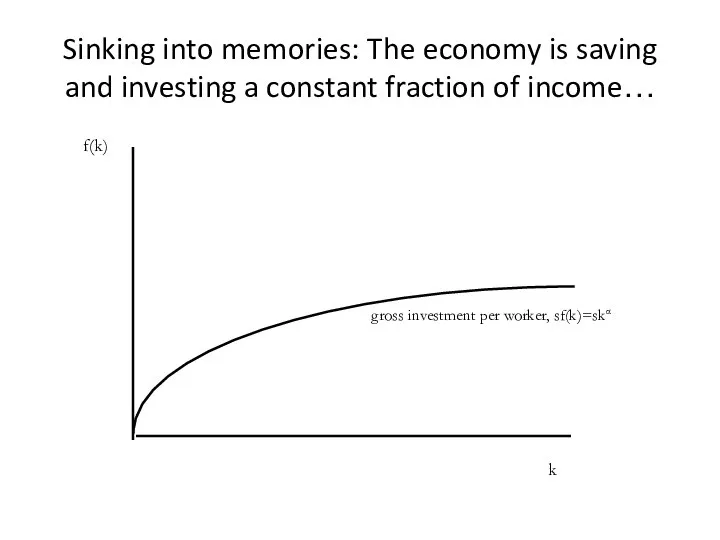
- 5. Sinking into memories: The economy is saving and investing a constant fraction of income… gross investment
- 6. Sinking into memories: What is “labor-augmenting technical progress”? This is technical progress that increases contribution of
- 7. Sinking into memories: If we take into account “labor-augmenting technical progress” that
- 8. Sinking into memories: Production function with technical progress in the intensive form
- 9. Sinking into memories: What is break-even investment?
- 10. Sinking into memories: Derivation of equilibrium capital per effective worker
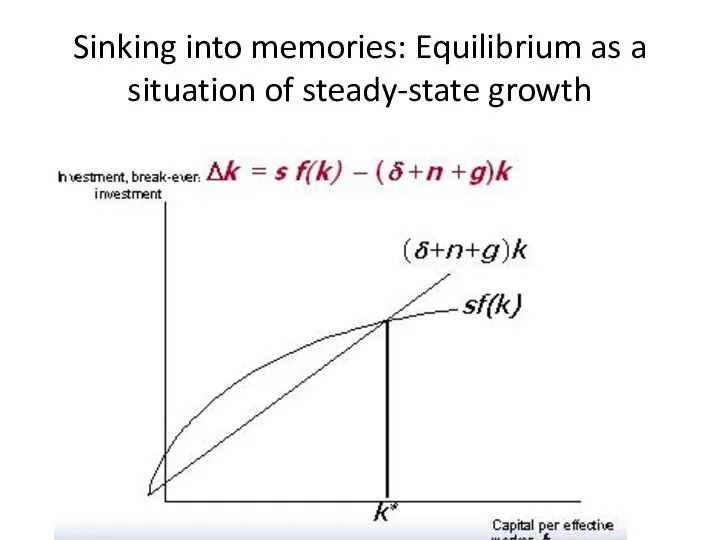
- 11. Sinking into memories: Equilibrium as a situation of steady-state growth
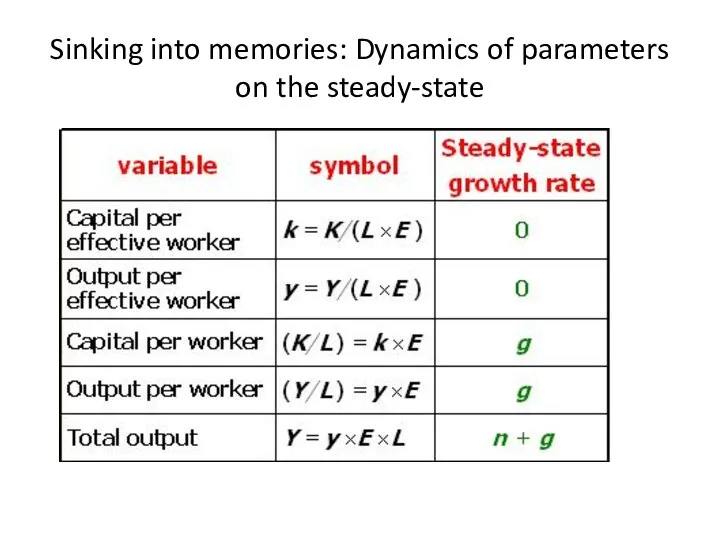
- 12. Sinking into memories: Dynamics of parameters on the steady-state
- 13. Sinking into memories: Balanced growth
- 14. Sinking into memories: Growth in steady state and outside steady state In the steady state –
- 15. Sinking into memories: Unconditional convergence
- 16. Sinking into memories: Conditional convergence
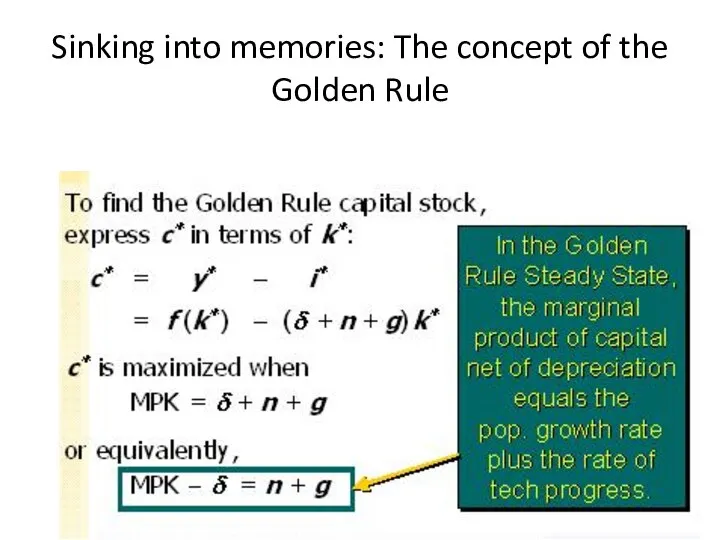
- 17. Sinking into memories: The concept of the Golden Rule
- 18. Sinking into memories: The Golden Rule – for what?
- 19. Sinking into memories: Accounting of growth in Solow model (Part 1)
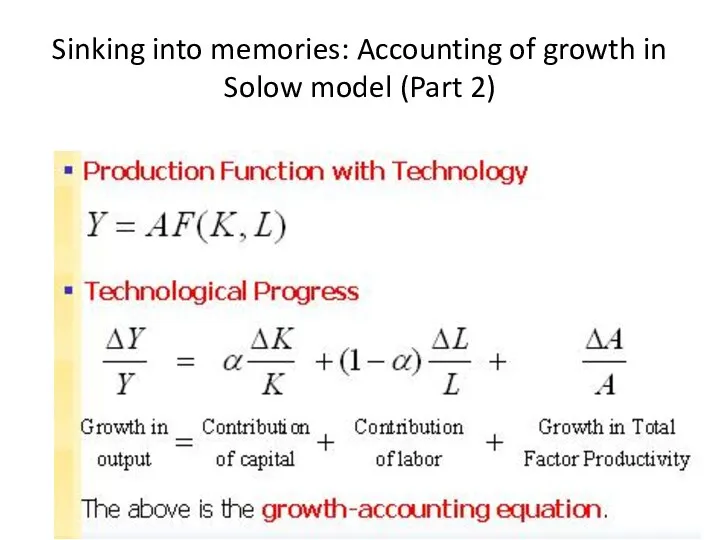
- 20. Sinking into memories: Accounting of growth in Solow model (Part 2)
- 21. Sinking into memories: Accounting of growth in Solow model (Part 3)
- 22. Accounting of growth in the U.S. economy In the end of the XX century
- 23. Accounting of growth among “Asian Tigers” In the end of the XX century
- 24. Exercise #1: the condition The savings rate = 0.3; the rate of population growth = 0.03;
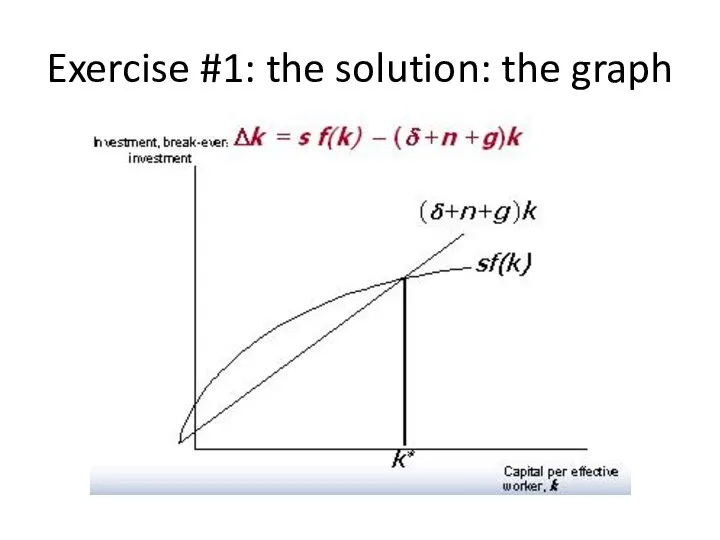
- 25. Exercise #1: the solution: the graph
- 26. Exercise #1: the solution: the figures If Y = K0.5(LE)0.5 Then y = k0.5 2) sy
- 27. Exercise #2: the condition The rate of population growth = 0.04; the rate of technical progress
- 28. Exercise #2: the solution: If Y = K0.5(LE)0.5 Then y = k0.5 2) sy = sk0.5
- 29. Exercise #2: the additional question Is this saving rate – 36% - consistent with the golden
- 30. Exercise #2: reply to the additional question Max c = (1 – s)y … If we
- 31. Exercise #3: the condition The savings rate = 0.48; the rate of population growth = 0.04;
- 32. Exercise #4: the condition The rate of population growth = 0.03; the rate of technical progress
- 34. Скачать презентацию

















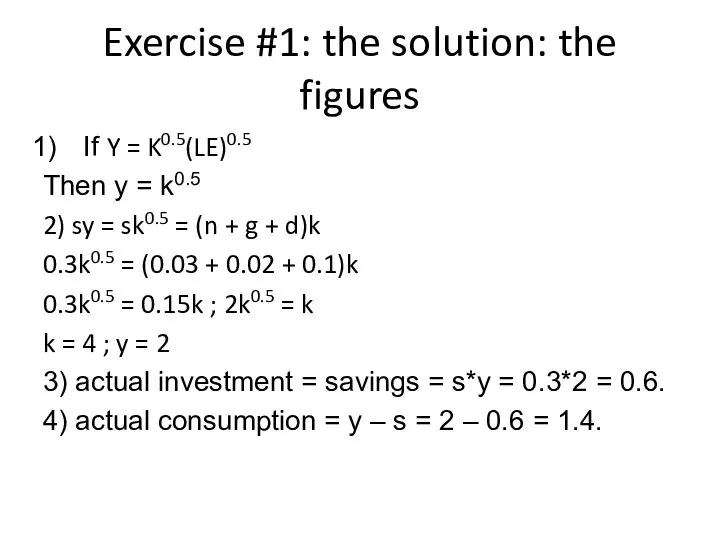

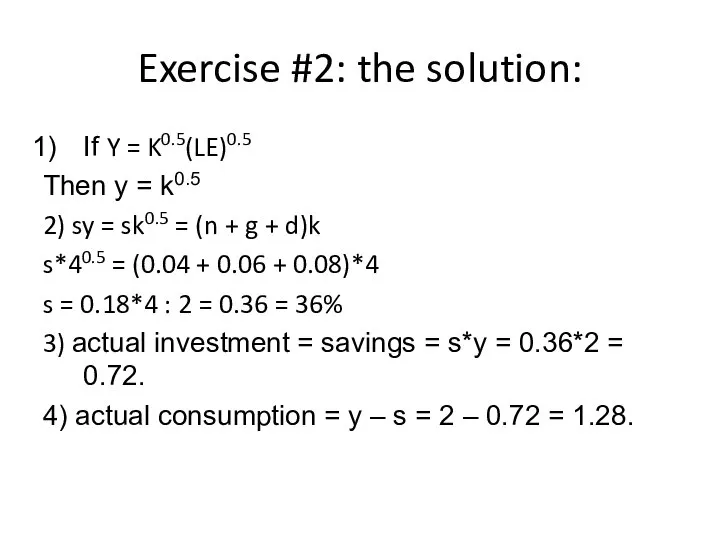




 Энергосервисные контракты в бюджетной сфере
Энергосервисные контракты в бюджетной сфере Статистика оборотного капитала
Статистика оборотного капитала Экономика
Экономика Государственный долг: причины возникновения и следствия
Государственный долг: причины возникновения и следствия Процесс живого стратегирования развития города – с участием жителей (от разработки до реализации)
Процесс живого стратегирования развития города – с участием жителей (от разработки до реализации) Методы микроэкономики
Методы микроэкономики Финансовый рынок России Выполнила: Гудимова К.С., Клеутина С.А., студентки группы МЭ091-092, ДС1
Финансовый рынок России Выполнила: Гудимова К.С., Клеутина С.А., студентки группы МЭ091-092, ДС1 Издержки производства, доход и прибыль фирмы
Издержки производства, доход и прибыль фирмы Влияние инфляции на уровень ВВП в странах с развивающейся экономикой
Влияние инфляции на уровень ВВП в странах с развивающейся экономикой Содержание экономической безопасности РФ Подготовила 4 подгруппа группы Т1202 Прутова О., Сембина А., Айтжан Д., Токманова С., Мынбол
Содержание экономической безопасности РФ Подготовила 4 подгруппа группы Т1202 Прутова О., Сембина А., Айтжан Д., Токманова С., Мынбол  Типы экономических систем
Типы экономических систем Безработица. Понятие, виды и показатели
Безработица. Понятие, виды и показатели Cущность и необходимость запасов на предприятии
Cущность и необходимость запасов на предприятии Мировые финансовые центры: роль и значение для мировой экономики Подготовила: Еросова Валерия, гр. МЭ-091
Мировые финансовые центры: роль и значение для мировой экономики Подготовила: Еросова Валерия, гр. МЭ-091 Безработица и ее формы
Безработица и ее формы Управление активами предприятия
Управление активами предприятия Экономическое развитие России в пореформенный период
Экономическое развитие России в пореформенный период Сравнение документов развития МСП в РФ
Сравнение документов развития МСП в РФ Основы организации деятельности предприятия
Основы организации деятельности предприятия Рынок
Рынок Основы экономики. Введение
Основы экономики. Введение Повышение экономической эффективности управления землями сельскохозяйственного назначения (на примере Республики Алтай)
Повышение экономической эффективности управления землями сельскохозяйственного назначения (на примере Республики Алтай) Финансовый рынок и его инструменты
Финансовый рынок и его инструменты Лекция №1.Т1
Лекция №1.Т1 Оплата труда
Оплата труда Накопление капитала и экономический рост. Тема 9
Накопление капитала и экономический рост. Тема 9 Тема 1. Предмет и метод экономической теории. Рыночная система
Тема 1. Предмет и метод экономической теории. Рыночная система Рыночный механизм
Рыночный механизм