Математические методы оценки взаимосвязи

Корреляционная связь -
это согласованное изменение двух признаков, отражающее, что изменчивость одного признака находится в соответствии с изменчивостью другого
«Когда изменяется X, то Y тоже меняется»
Не путать с причинно-следственной связью!

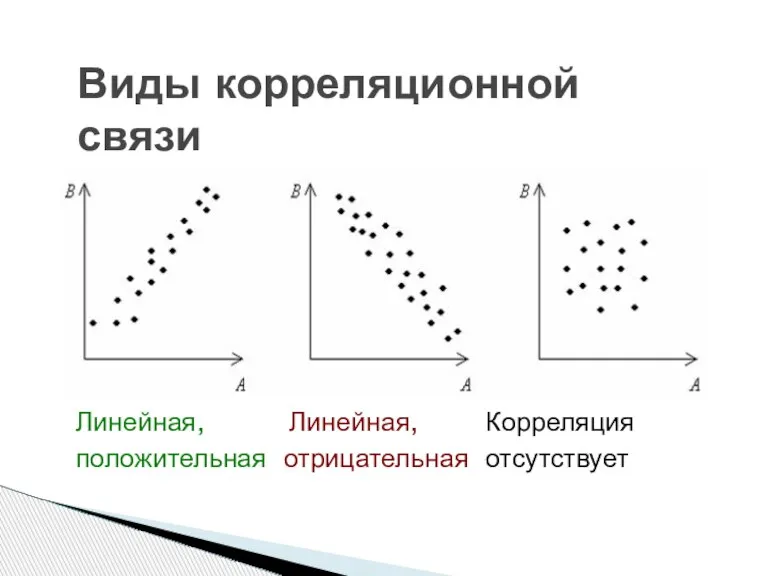
Виды корреляционной связи
Линейная, Линейная, Корреляция
положительная отрицательная отсутствует

Сила корреляционной связи
Выражается через значение коэффициента корреляции (R)
Бывает:
R(а,b)>0,70 - сильная связь между a и b
0,5
0,3
0,2
R<0,2 - очень слабая

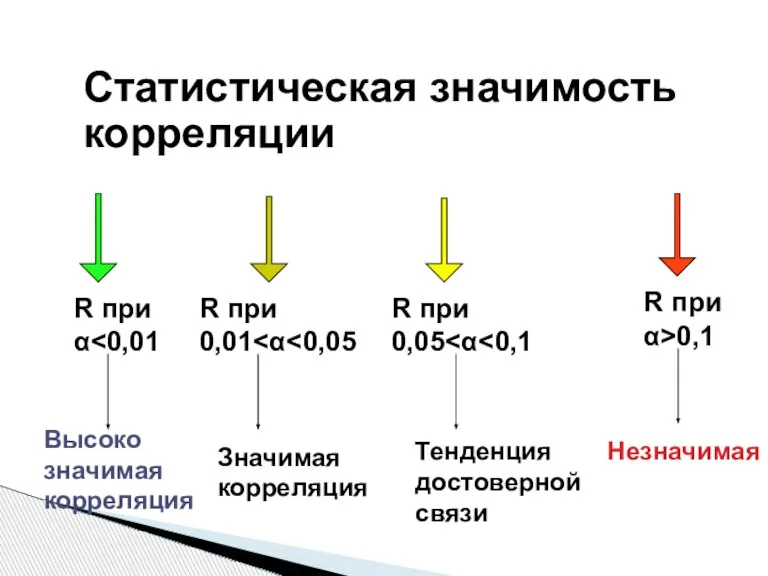
Статистическая значимость корреляции
R при α<0,01
Высоко значимая
корреляция
R при 0,01<α<0,05
R при 0,05<α<0,1
Значимая
корреляция
R при α>0,1
Тенденция достоверной связи
Незначимая

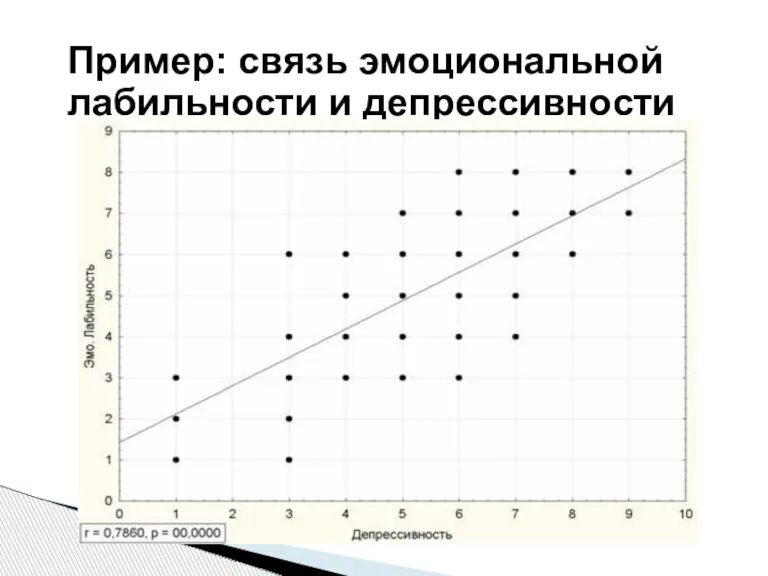
Пример: связь эмоциональной лабильности и депрессивности

для параметрических шкал - коэффициент Rx,y Пирсона
для данных ранговой и параметрических шкал - Rs Спирмена
для данных ранговых шкал — τ (тау) критерий Кендалла
для дихотомических шкал - φ коэффициент ассоциации Пирсона
Коэффициенты корреляции

Коэффициент корреляции Rx,y_Пирсона
где xi и yi — показатели под номером i,
X и Y — средние
Ограничения: параметрические данные; нормальное распределение в обеих выборках; 5>nx,ny>5000; nx=ny
Возможности: определяет силу и направление корреляционной связи между двумя признаками (измеренными в одной и той же группе или между двумя рядами значений, полученных в двух группах)

Коэффициент корреляции
Rs Спирмена
n – количество пар рангов,
d – разность между рангами по X и по Y
Возможности: измеряет силу и направление корреляционной связи; работает со всеми количественными данными; непараметрический.
Ограничения: 5< n< 40 (таблицы); при увеличении n становится менее мощным; требует поправок для связанных рангов

1. В таблице 1,2 столбцы заполнить значениями X и Y
2. В столбце 3 присвоить ранги значениям X по Правилам ранжирования. Аналогично для значений Y (в столбце 4)
3. Разности между каждой парой рангов (по строчка) занести в 5-й столбец как d
4. Возвести каждую разность в квадрат, записать в 6-й столбец как d2
5. Посчитать сумму всех d2, записать ее как ∑(d2)=
Алгоритм расчета Rs Спирмена

6. Считать значение коэффициента:
7. При наличии
связанных рангов
в числитель дроби сделать поправки +Tx и +Ty:
где ax и by — объем каждой группы одинаковых рангов в соответствующем ранговом ряду
Алгоритм расчета Rs Спирмена

8. Определить по таблицам критические значения; сопоставить с Rs
9. Если Rs попадает в интервал p<0,01 признать имеющуюся корреляцию статистически высоко значимой
10. Сделать статистический вывод
Алгоритм расчета Rs Спирмена