- Главная
- Экономика
- Механизмы коллективной ответственности, или как заставить всех честно платить налоги

Содержание
- 2. Что изучает экономическая наука 2 Наука – поиск закономерностей, прогнозирование и управление на их основе Естественные
- 3. Равновесие и общественный оптимум 3 Дилемма заключенных: 1. Равновесие ≠ общественный оптимум. 2. Равновесий может быть
- 4. Простые и не очень механизмы 4 Простейший механизм – изменение цены. Скидки – увеличивают продажи, но
- 5. Пример «Зайцы в электричке» 5 Ответ: «пофамильный принцип» упорядочения людей приводит к равновесию Нэша, в котором
- 6. Пример «Неплательщики налогов» 6 2000 – большинство не платит налогов! ## 70% предприятий торговли показывают убытки.
- 7. Механизмы наказания 7 Механизм 1 «Зверские штрафы»: pi = 1/n, T > nbmax. Проблемы: политическая неприемлемость,
- 8. Наводящий пример – 1 8 Наводящий пример 1: b = 4/3Т, T = 3/4b. Не проверять
- 9. Наводящий пример – 2 9 Наводящий пример 2: T = 1, b1=0,2, b2=0,3, b3=0,4, b4=0,9. Можно
- 10. Многоступенчатая стратегия 10 Заданы барьеры: 0 ≤ z1 Заданы вероятности проверок в каждой группе: λ1,…,λk: Σ
- 12. Скачать презентацию
Слайд 2Что изучает экономическая наука
2
Наука – поиск закономерностей, прогнозирование и управление на их
Что изучает экономическая наука
2
Наука – поиск закономерностей, прогнозирование и управление на их

Естественные науки – точные законы.
Социальные науки – свобода действий участников взаимодействия.
Предположение экономики – рациональное поведение агентов.
Фирмы – максимизируют прибыль.
Потребители – максимизируют полезность.
Идеальное государство – максимизирует общественное благосостояние.
Реальные чиновники – максимизируют некоторую функцию выигрыша
(экономический рост + власть + прямые и косвенные доходы +…)
Наблюдения → теоретическая модель → эмпирическая проверка
(теория игр) (эконометрика)
Проверка непроста! Множество факторов, воздействующих на результат.
Спрос ? цена, другие цены, доходы, реклама, сезонность.
Рост ? текущий уровень, образование, население, институты, инфляция.
Слайд 3Равновесие и
общественный оптимум
3
Дилемма заключенных:
1. Равновесие ≠ общественный оптимум.
2. Равновесий может быть много.
Равновесие
Равновесие и
общественный оптимум
3
Дилемма заключенных:
1. Равновесие ≠ общественный оптимум.
2. Равновесий может быть много.
Равновесие
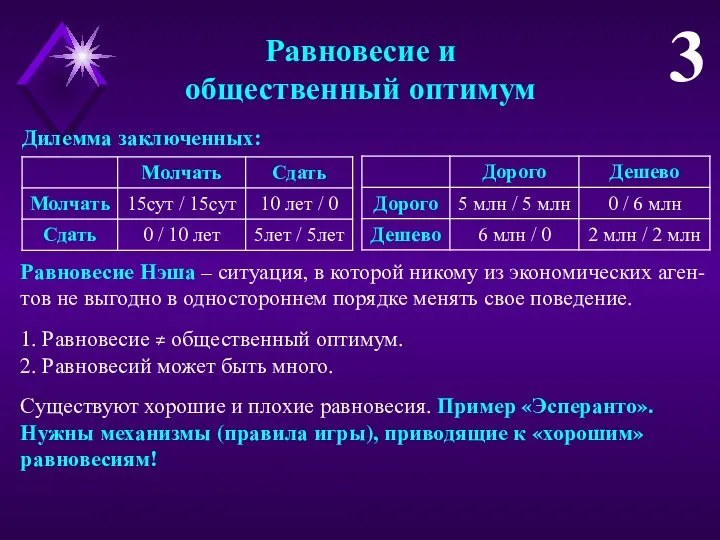
Существуют хорошие и плохие равновесия. Пример «Эсперанто».
Нужны механизмы (правила игры), приводящие к «хорошим» равновесиям!
Слайд 4Простые и не очень механизмы
4
Простейший механизм – изменение цены.
Скидки – увеличивают продажи,
Простые и не очень механизмы
4
Простейший механизм – изменение цены.
Скидки – увеличивают продажи,

Необходимы количественные оценки (в т.ч. эластичность)
Пример: p ↓ на 30%, q ↑ на 40%. Полезна ли такая распродажа?
«Найдите цену ниже, и мы продадим Вам товар по этой цене»
Выгоден ли потребителям? Выгоден ли фирмам?
Другие примеры:
Кому выдать лицензии на деятельность и как при этом собрать миллиарды долларов? Аукционы.
Как распределить между участниками прибыли или издержки? Вектор Шепли.
Как принять абитуриентов в вузы, чтобы никто не остался недо-вольным? Мэтчинги.
Как заставить всех налогоплательщиков честно платить налоги? Коллективная ответственность.
Слайд 5Пример «Зайцы в электричке»
5
Ответ: «пофамильный принцип» упорядочения людей приводит к равновесию Нэша,
Пример «Зайцы в электричке»
5
Ответ: «пофамильный принцип» упорядочения людей приводит к равновесию Нэша,

Общая постановка: как решить задачу контроля в условиях малого числа проверяющих.
Частная постановка: полицейский может гарантированно поймать и оштрафовать одного нарушителя, перепрыгнувшего через турникет, но только одного!
Два равновесия Нэша:
«Хорошее» равновесие: никто не прыгает (невыгодно прыгать, т.к. поймают и оштрафуют гарантированно!)
«Плохое» равновесие: прыгают все (невыгодно платить, т.к. шансы быть пойманным очень невелики)
Как перейти из «плохого» равновесия в «хорошее»?
Слайд 6Пример «Неплательщики налогов»
6
2000 – большинство не платит налогов!
## 70% предприятий торговли показывают
Пример «Неплательщики налогов»
6
2000 – большинство не платит налогов!
## 70% предприятий торговли показывают

При этом строятся сверкающие бизнес-центры из стекла и бетона.
Критерий инспектора: ui (xi, x–i) = bixi – T pi (x1,…,xn) xi → max.
Модель:
i = 1,…,n – отрасли, проверяемые рациональными, но потенциально коррумпированными налоговыми инспекторами.
x1,…,xn ∈ [0;1] – уровень коррупции в отрасли (известный, но сло-жно доказуемый, заданный экспертными оценками)
Возможна одна единственная честная проверка, но вероятность ее проведения можно поставить в зависимость от вектора x.
p1(x),…,pn(x) ∈ [0;1] – вероятности проверок
Σ pj(x) ≤ 1, при некоторых x можно никого не проверять: Σ pj(x) < 1.
p1(x),…,pn(x) – «взяткоемкость» отраслей, Т – штраф.
Слайд 7Механизмы наказания
7
Механизм 1 «Зверские штрафы»:
pi = 1/n, T > nbmax.
Проблемы: политическая неприемлемость,
Механизмы наказания
7
Механизм 1 «Зверские штрафы»:
pi = 1/n, T > nbmax.
Проблемы: политическая неприемлемость,

Механизм 2 «Наказать самого наглого»
Строгое упорядочение всех инспекторов и проверка первого из списка, у кого xi > 0.
Проблемы: асимметричность («неполиткорректность») процедуры, не-устойчивость к сговору даже без побочных платежей.
Можно ли сделать что-то?
Наводящий пример 1: можно ли уменьшить уровень коррупции при больших взятках и низких штрафах, например, при b = 4/3Т ?
Слайд 8Наводящий пример – 1
8
Наводящий пример 1:
b = 4/3Т, T = 3/4b.
Не проверять
Наводящий пример – 1
8
Наводящий пример 1:
b = 4/3Т, T = 3/4b.
Не проверять

Стратегия 1
x = 1, u = b – 3/4b = 0,25b.
Стратегия 2
x = 0,3, u = 0,3b > 0,25b.
Ступенчатая стратегия наказания снижает уровень коррупции больше, чем в 3 раза!
Наводящий пример 2: T = 1, b1=0,2, b2=0,3, b3=0,4, b4=0,9.
Можно ли искоренить коррупцию полностью?
Слайд 9Наводящий пример – 2
9
Наводящий пример 2: T = 1, b1=0,2, b2=0,3, b3=0,4,
Наводящий пример – 2
9
Наводящий пример 2: T = 1, b1=0,2, b2=0,3, b3=0,4,

Можно ли искоренить коррупцию полностью?
Решение: приходим с равной вероятностью ко всем, у кого xi > 0
Первый: (0,2 – 0,25) x1 < 0, брать взятки невыгодно, x1 = 0.
Второй: (0,3 – 0,33) x2 < 0, брать взятки невыгодно, x2 = 0.
Третий: (0,4 – 0,5) x3 < 0, брать взятки невыгодно, x3 = 0.
Четвертый: (0,9 – 1) x4 < 0, брать взятки невыгодно, x4 = 0.
Могут быть многоступенчатые стратегии наказания:
при уровне коррупции ниже определенной величины проверки совсем не проводятся, при его превышении – с малой вероятностью, дальше больше и т.д.
Слайд 10Многоступенчатая стратегия
10
Заданы барьеры: 0 ≤ z1 < z2 < … < zk
Многоступенчатая стратегия
10
Заданы барьеры: 0 ≤ z1 < z2 < … < zk

Заданы вероятности проверок в каждой группе: λ1,…,λk: Σ λl = 1.
Вероятность проверки для i-инспектора:
Доказано:
При любых наборах z и λ такая стратегия реализуется через сильное равновесие Нэша (устойчивое к сговору).
Соответствующее равновесие эффективно вычисляется простейшей процедурой.
Достаточно рассматривать n-ступенчатые стратегии.
 Passenger traffic at Moscow airports in August grew by almost 1.5 times compared to July
Passenger traffic at Moscow airports in August grew by almost 1.5 times compared to July Оптимизация структуры капитала предприятия розничной торговли ПАО Магнит
Оптимизация структуры капитала предприятия розничной торговли ПАО Магнит Бюджет и бюджетная система РФ
Бюджет и бюджетная система РФ Общие вопросы организации внешнеэкономической деятельности
Общие вопросы организации внешнеэкономической деятельности Мероприятие по разработке систем энергосбережения в средствах размещения
Мероприятие по разработке систем энергосбережения в средствах размещения Деятельность государственного сектора экономики: измерение масштабов и эффективности
Деятельность государственного сектора экономики: измерение масштабов и эффективности Законодательное собрание Вологодской области. Итоги четырнадцатой сессии
Законодательное собрание Вологодской области. Итоги четырнадцатой сессии Формы организации бизнеса
Формы организации бизнеса Макроэкономические процессы. Измерители экономики
Макроэкономические процессы. Измерители экономики Международное разделение труда
Международное разделение труда международная экономика
международная экономика Предпринимательство в экономической структуре общества
Предпринимательство в экономической структуре общества Кооперативная теория игр
Кооперативная теория игр Трудовые ресурсы и их влияние на эффективность деятельность предприятия
Трудовые ресурсы и их влияние на эффективность деятельность предприятия Глобализация
Глобализация Семинар № 2. Почему динамика продаж автомобилей считается одним из лучших показателей роста экономики?
Семинар № 2. Почему динамика продаж автомобилей считается одним из лучших показателей роста экономики? Влияние экономики на жизнь студента
Влияние экономики на жизнь студента Comprehensive urban planing
Comprehensive urban planing Глобализация мирохозяйственных связей
Глобализация мирохозяйственных связей Миграционная ситуация в России
Миграционная ситуация в России Экономика и ее основные участники (7 класс)
Экономика и ее основные участники (7 класс) Мировое хозяйство в ХХ - начале XXI века
Мировое хозяйство в ХХ - начале XXI века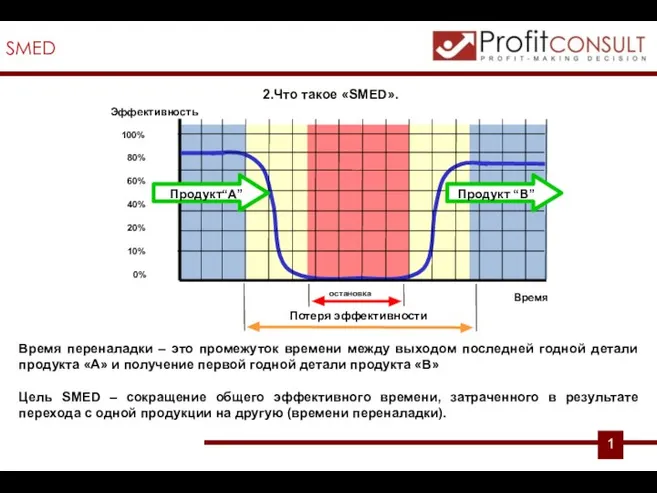 SMED (Single Minute Exchange of Dies). Быстрая переналадка
SMED (Single Minute Exchange of Dies). Быстрая переналадка Измерители экономического роста
Измерители экономического роста Тема 12. Международные экономические отношения
Тема 12. Международные экономические отношения Основные макроэкономические проблемы. Валовой внутренний продукт
Основные макроэкономические проблемы. Валовой внутренний продукт Теоретические основы социально-экономической статистики
Теоретические основы социально-экономической статистики Типы рыночных структур
Типы рыночных структур