Содержание
- 2. Аксиомы рациональности поведения потребителя Обычно от ординалистской, или порядковой, функции предпочтений экономического субъекта требуют, чтобы она
- 3. Теорема Дебре в слабой форме Если множество X качественно сравнимых наборов благ, которое должно быть замкнутым
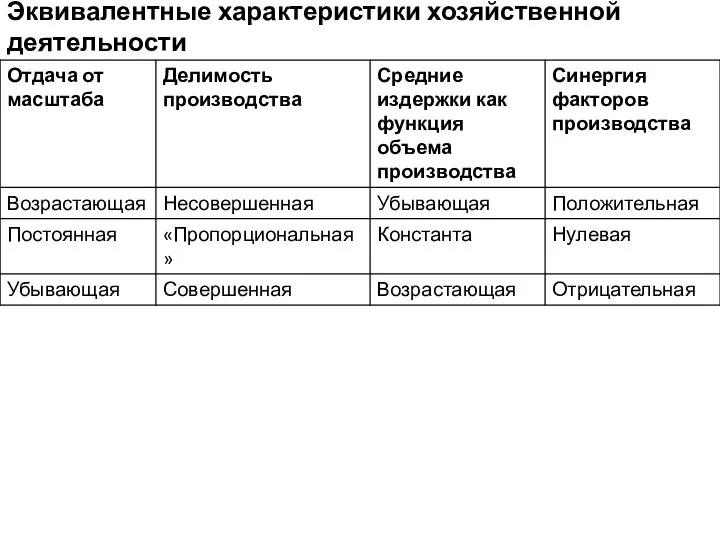
- 4. Отдача от масштаба и делимость производства Эквивалентность возрастающей отдачи от масштаба и несовершенной делимости производства: Эквивалентные
- 5. Отдача от масштаба и поведение средних издержек y=f(x) x=(xK,xL) TC(y)=TC(xK,xL) Факторизация издержек: Линейная однородность функции издержек
- 6. Отдача от масштаба и поведение средних издержек (однородная технология) Функция называется однородной степени γ, если для
- 7. Отдача от масштаба и поведение средних издержек (однородная технология) Таким образом, функция издержек имеет степенной вид
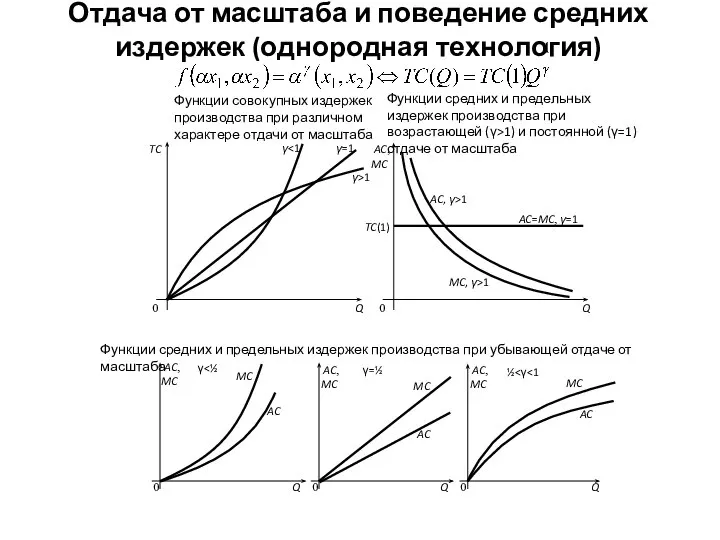
- 8. Отдача от масштаба и поведение средних издержек (однородная технология) Функции совокупных издержек производства при различном характере
- 9. Эквивалентные характеристики хозяйственной деятельности
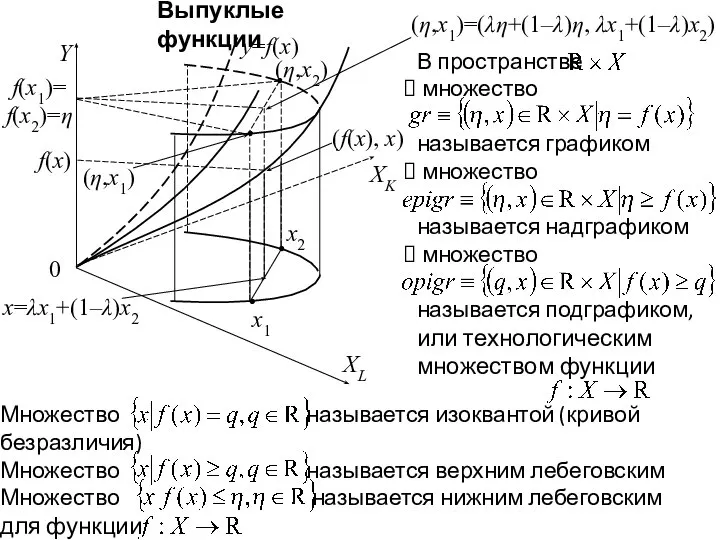
- 10. В пространстве множество называется графиком множество называется надграфиком множество называется подграфиком, или технологическим множеством функции Выпуклые
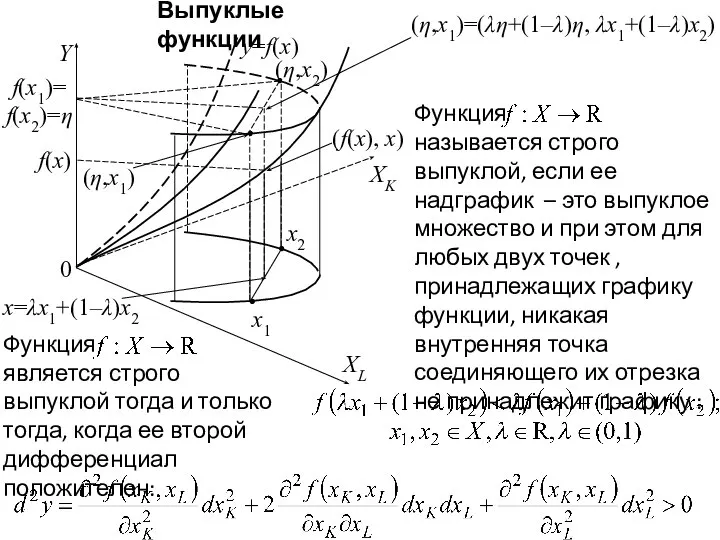
- 11. Выпуклые функции f(x) f(x1)= f(x2)=η (η,x2) y=f(x) (f(x), x) (η,x1)=(λη+(1–λ)η, λx1+(1–λ)x2) x=λx1+(1–λ)x2 XK Y x2 XL
- 12. Выпуклые функции f(x) f(x1)= f(x2)=η (η,x2) y=f(x) (f(x), x) (η,x1)=(λη+(1–λ)η, λx1+(1–λ)x2) x=λx1+(1–λ)x2 XK 0 Y x2
- 13. Выпуклые функции f(x) f(x1)= f(x2)=η (η,x2) y=f(x) (f(x), x) (η,x1)=(λη+(1–λ)η, λx1+(1–λ)x2) x=λx1+(1–λ)x2 XK Y x2 XL
- 14. Выпуклые функции f(x) f(x1)= f(x2)=η (η,x2) y=f(x) (f(x), x) (η,x1)=(λη+(1–λ)η, λx1+(1–λ)x2) x=λx1+(1–λ)x2 XK 0 Y x2
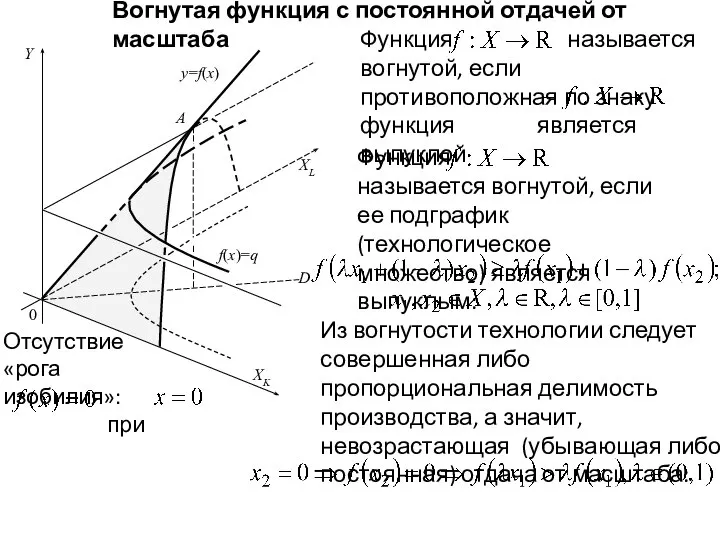
- 15. Y XL XK y=f(x) 0 f(x)=q A D Вогнутая функция с постоянной отдачей от масштаба Функция
- 16. Y XL XK y=f(x) 0 f(x)=q A D Вогнутая функция с постоянной отдачей от масштаба Функция
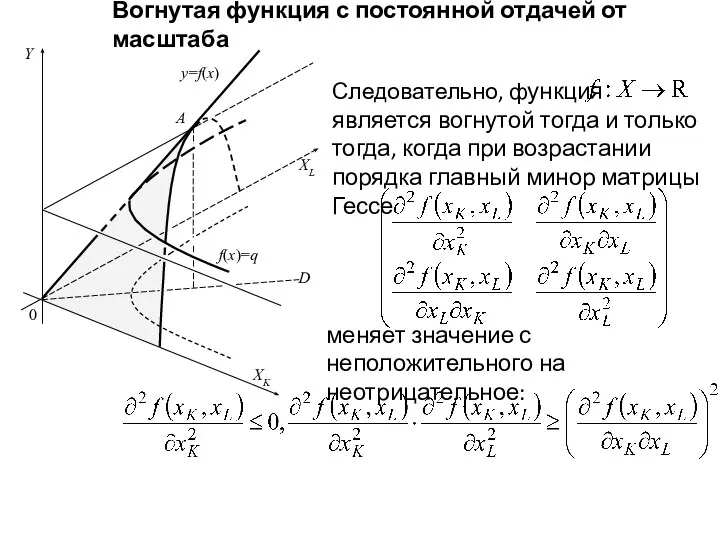
- 17. Y XL XK y=f(x) 0 f(x)=q A D Вогнутая функция с постоянной отдачей от масштаба Следовательно,
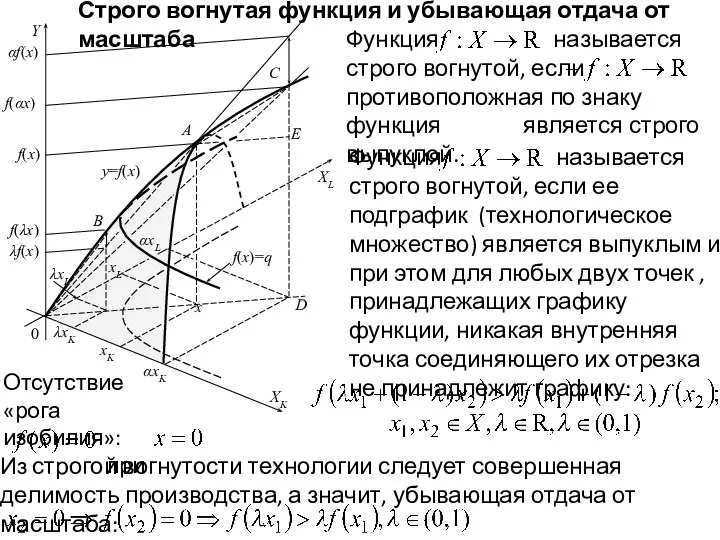
- 18. XL C f(x)=q Y XK y=f(x) 0 A D B xL xK λxK αxK αxL λxL
- 19. XL C f(x)=q Y XK y=f(x) 0 A D B xL xK λxK αxK αxL λxL
- 20. XL C f(x)=q Y XK y=f(x) 0 A D B xL xK λxK αxK αxL λxL
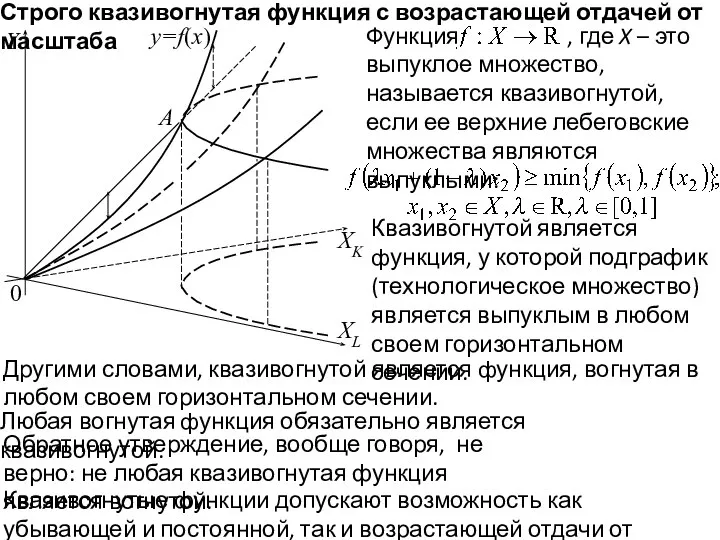
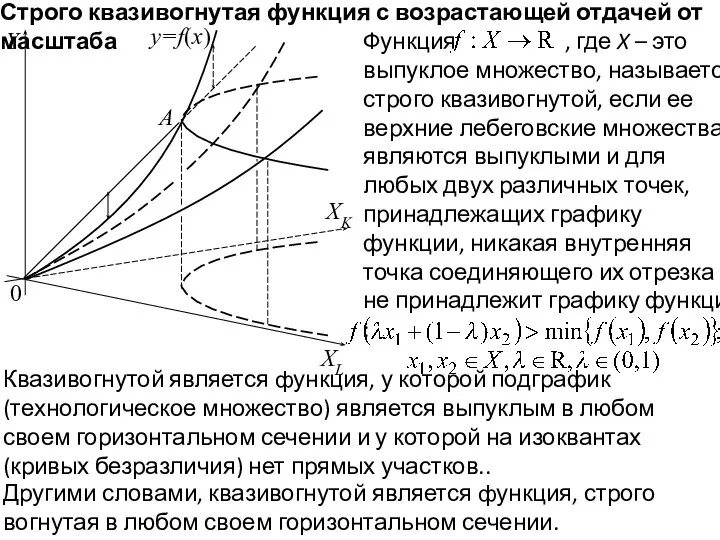
- 21. 0 Y y=f(x) XK XL A Строго квазивогнутая функция с возрастающей отдачей от масштаба Функция ,
- 22. 0 Y y=f(x) XL A Строго квазивогнутая функция с возрастающей отдачей от масштаба Функция является квазивогнутой
- 23. 0 Y y=f(x) XL A Строго квазивогнутая функция с возрастающей отдачей от масштаба Функция , где
- 24. 0 Y y=f(x) XL A Строго квазивогнутая функция с возрастающей отдачей от масштаба Выражение в левой
- 25. 0 Y y=f(x) XK A Строго квазивогнутая функция с возрастающей отдачей от масштаба Другими словами, квазивогнутой
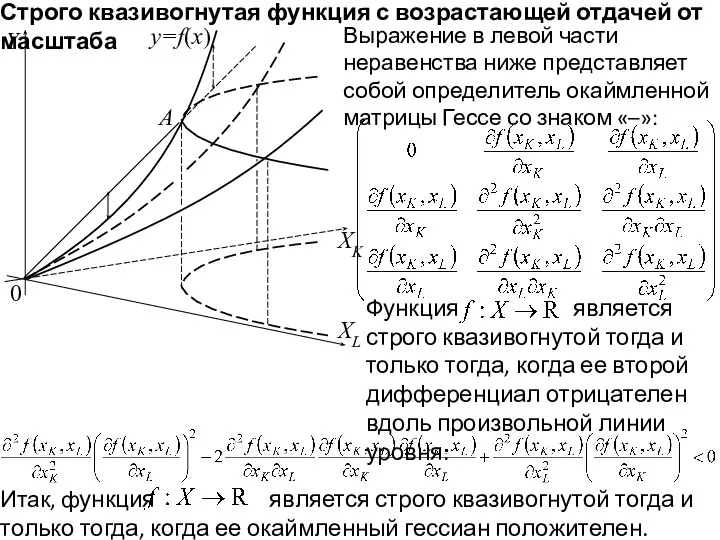
- 26. 0 Y y=f(x) XK A Строго квазивогнутая функция с возрастающей отдачей от масштаба Функция , где
- 27. 0 Y y=f(x) A Строго квазивогнутая функция с возрастающей отдачей от масштаба XK XL Функция является
- 28. 0 Y y=f(x) A Строго квазивогнутая функция с возрастающей отдачей от масштаба XK XL Функция является
- 30. Скачать презентацию

















 Бюджетный процесс в Российской Федерации
Бюджетный процесс в Российской Федерации Коммуникации в менеджменте
Коммуникации в менеджменте Безработица равна 100%, если безработный – это Вы
Безработица равна 100%, если безработный – это Вы Термины в микроэкономике. IТ для решения экономических задач
Термины в микроэкономике. IТ для решения экономических задач Сущность, цели и задачи рекламы. Функции и классификация рекламы
Сущность, цели и задачи рекламы. Функции и классификация рекламы Эколого-экономическая безопасность в новых условиях развития арктической зоны РФ
Эколого-экономическая безопасность в новых условиях развития арктической зоны РФ Podmioty globalizacji - państwa narodowe
Podmioty globalizacji - państwa narodowe Введение в микроэкономику: предмет экономики и основные понятия. 2018
Введение в микроэкономику: предмет экономики и основные понятия. 2018 Центры индустриальной медицины
Центры индустриальной медицины Экономика Челябинской области
Экономика Челябинской области Социальные груп-пы в организации и управление груп-повым поведе-нием
Социальные груп-пы в организации и управление груп-повым поведе-нием Валютный рынок и конвертируемость валют
Валютный рынок и конвертируемость валют Методология исследования А. Маршалла
Методология исследования А. Маршалла Faktory_proizvodstva
Faktory_proizvodstva Общественные формы организации производства
Общественные формы организации производства Общая и предельная полезность. Закон убывающей полезности
Общая и предельная полезность. Закон убывающей полезности Учет и контроль в управлении бизнесом
Учет и контроль в управлении бизнесом Дух предпринимательства преобразует экономику
Дух предпринимательства преобразует экономику Учёт и анализ движения, состояния и эффективности использования основных средств
Учёт и анализ движения, состояния и эффективности использования основных средств Классификация стран мира
Классификация стран мира Основы предпринимательства и предпринимательской деятельности
Основы предпринимательства и предпринимательской деятельности Издержи и прибыль коммерческого банка.
Издержи и прибыль коммерческого банка. Прогнозирование в электроэнергетике
Прогнозирование в электроэнергетике Мировые кризисы
Мировые кризисы Производство экономических благ. Лекция 4
Производство экономических благ. Лекция 4 Общее собрание собственников помещений в многоквартирном доме
Общее собрание собственников помещений в многоквартирном доме Естественная монополия и ее регулирование: от теории к российской практике
Естественная монополия и ее регулирование: от теории к российской практике Realizowanie obrotu towarowego
Realizowanie obrotu towarowego