Вероятностные модели управления запасами

Введем следующие обозначения.
▪ L — срок выполнения заказа, т.е. время от момента размещения заказа до его поставки; ▪ X1— случайная величина, представляющая величину спроса на протяжении срока выполнения заказа;
▪ μ1 — средняя величина спроса на протяжении срока выполнения заказа,
▪ σ1 — среднеквадратическое отклонение величины спроса на протяжении срока выполнения заказа;
▪ В — размер резервного запаса;
▪ α — максимально возможное значение вероятности истощения запаса на протяжении срока выполнения заказа.
Основным предположением при построении модели является то, что величина спроса Х1 на протяжении срока выполнения заказа L является нормально распределенной случайной величиной со средним μ1и стандартным отклонением σ1 т.е. имеет распределение N(μ1,σ1)

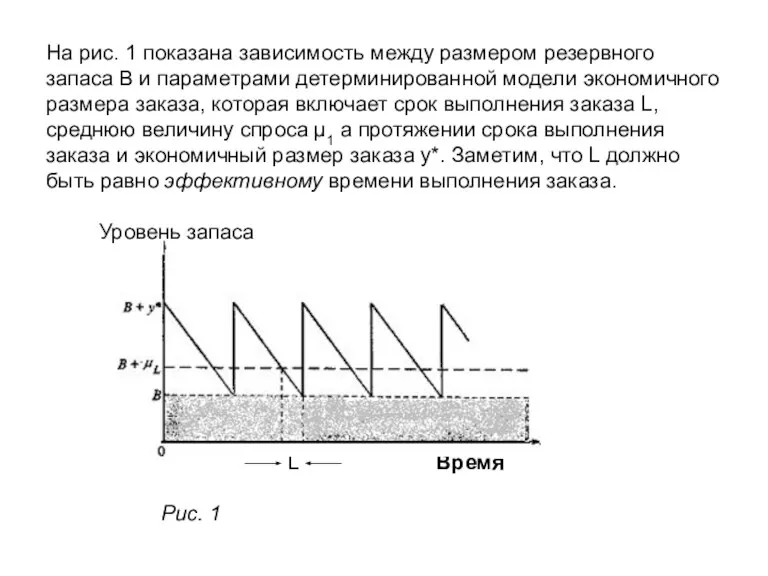
На рис. 1 показана зависимость между размером резервного запаса В и параметрами детерминированной модели экономичного размера заказа, которая включает срок выполнения заказа L, среднюю величину спроса μ1 а протяжении срока выполнения заказа и экономичный размер заказа у*. Заметим, что L должно быть равно эффективному времени выполнения заказа.
Уровень запаса
L Время
Рис. 1

Вероятностное условие, которое определяет размер резервного запаса В, имеет вид:
По определению случайная величина
является нормированной нормально распределенной случайной величиной, т.е. имеет распределение N(0, 1). Следовательно,
На рис. 2 показана величина , которая определяется из таблицы стандартного нормального распределения, так что
Следовательно, размер резервного запаса должен удовлетворять неравенству B≥σL .

Величина спроса на протяжении срока выполнения заказа L обычно описывается плотностью распределения вероятностей, отнесенной к единице времени (например, к дню или неделе), из которой можно определить распределение спроса на протяжен периода L. В частности, если спрос за единицу времени является нормально распределенной случайной величиной со средним D и стандартным отклонением σ, то общий спрос на протяжении срока выполнения заказа L будет иметь распределение N(μL, σL), где μL=DL и σL= . Формула для σL получена на основании того, что значение L является целым числом (или же округлено до целого числа).
1.2. Стохастический вариант модели экономичного размера заказа
"Рандомизированная" модель экономичного размера заказа не дает оптимальную политику управления запасами. Информация, имеющая отношение к вероятностной природе спроса первоначально не учитывается, а используется лишь независимо на последнем этапе вычислений. Рассмотрим более точную модель, в которой вероятностная природа спроса учитывается непосредственно в постановке задачи.

В новой модели допускается неудовлетворенный спрос (рис. 3). Заказ размером у размещается тогда, когда объем запаса достигает уровня R. Как и в детерминированном случае, уровень R, при котором снова размещается заказ, является функцией периода времени между размещением заказа и его выполнением. Оптимальные значения у и R определяются минимизацией ожидаемых затрат системы управления запасами, отнесенных к единице времени; они включают расходы на размещение заказа, на хранение, так и потери, связанные с неудовлетворенным спросом.
Рис. 3

В рассматриваемой модели приняты три допущения.
1. Неудовлетворенный в течение срока выполнения заказа спрос накапливается.
2. Разрешается не более одного невыполненного заказа.
3. Распределение спроса в течение срока выполнения заказа является стационарным (неизменным) во времени.
Для определения функции, отражающей суммарные затраты, отнесенные к единице времени, введем следующие обозначения.
▪ f(x) — плотность распределения спроса х в течение срока выполнения заказа,
▪ D — ожидаемое значение спроса в единицу времени, ▪ h — удельные затраты на хранение (на единицу продукции за единицу времени),
▪ р — удельные потери от неудовлетворенного спроса (на единицу продукции за единицу времени),
▪ К — стоимость размещения заказа.

Основываясь на этих определениях, вычислим компоненты функции затрат.
1. Стоимость размещения заказов. Приближенное число заказов в единицу времени равно D/y, так что стоимость размещения заказов в единицу времени равна KD/y.
2. Ожидаемые затраты на хранение. Средний уровень запаса равен
Следовательно, ожидаемые затраты на хранение за единицу времени равны hI.
Приведенная формула получена в результате усреднения ожидаемых запасов в начале и конце временного цикла, т.е. величин у + M{R-х} и M{R-х} соответственно. При этом игнорируется случай, когда величина R - М{х} может быть отрицательной, что является одним из упрощающих допущений рассматриваемой модели.

3. Ожидаемые потери, связанные с неудовлетворенным спросом.
Дефицит возникает при х > R. Следовательно, ожидаемый дефицит за единицу времени равен
Так как в модели предполагается, что р пропорционально лишь объему дефицита, ожидаемые потери, связанные с неудовлетворенным спросом, за один цикл равны pS. Поскольку единица времени содержит D/y циклов, то ожидаемые потери, обусловленные дефицитом, составляют pDS/y за единицу времени.
Результирующая функция общих потерь за единицу времени TCU имеет следующий вид.

Оптимальные значения у* и R* определяются из представленных ниже уравнений.
Следовательно, имеем
(1) (2)
Так как из уравнений (1) и (2) у* и R* нельзя определить в явном виде, для их нахождения используется численный алгоритм, предложенный Хедли и Уайтин (Hadley, Whitin) [1]. Доказано, что алгоритм сходится за конечное число итераций при условии, что допустимое решение существует.

При R = 0 последние два уравнения соответственно дают следующее.
Если ≥ , тогда существуют единственные оптимальные значения для у и R. Вычислительная процедура определяет, что наименьшим значением у* является , которое достигается при S = 0.
Алгоритм состоит из следующих шагов.
Шаг 0. Принимаем начальное решение и считаем R0 = 0. Полагаем i = 1 и переходим к шагу i.
Шаг i. Используем значение уi для определения Ri, из уравнения (2). Если Ri≈ R i-1, вычисления заканчиваются; оптимальным решением считаем у* = уi и R* = Ri. Иначе используем значение Ri в уравнении (1) для вычисления уi. Полагаем i=i+1 и повторяем шаг i.

2. Одноэтапные модели
Одноэтапные модели управления запасами отражают ситуацию, когда для удовлетворения спроса в течение определенного периода продукция заказывается только один раз. Например, модный сезонный товар устаревает к концу сезона, и, следовательно, заказы на него могут не возобновляться. В данном разделе рассматривается два типа таких моделей: с учетом и без учета затрат на оформление заказов.
При изложении данного материала используются следующие обозначения.
с — стоимость закупки (или производства) единицы продукции,
К — стоимость размещения заказа,
h — удельные затраты на хранение единицы продукции в течение рассматриваемого периода,
р — удельные потери от неудовлетворенного спроса (на единицу продукции за рассматриваемый период),
D — величина случайного спроса за рассматриваемый период,
f(D) — плотность вероятности спроса за рассматриваемый период,
у — объем заказа,
х — наличный запас продукта перед размещением заказа.
Модель определяет оптимальный объем заказа у, который минимизирует суммарные ожидаемые затраты, связанные с закупкой (или производством), хранением и неудовлетворенным спросом. При известном оптимальном значении у (обозначается у*) оптимальное управление запасами состоит в размещении заказа объемом у* - х, если х < y; в противном случае заказ не размещается.

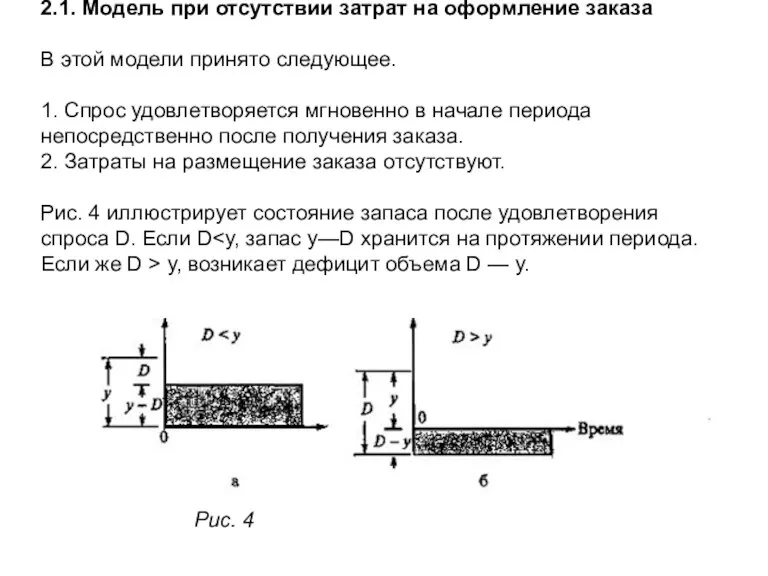
2.1. Модель при отсутствии затрат на оформление заказа
В этой модели принято следующее.
1. Спрос удовлетворяется мгновенно в начале периода непосредственно после получения заказа.
2. Затраты на размещение заказа отсутствуют.
Рис. 4 иллюстрирует состояние запаса после удовлетворения спроса D. Если D
у, возникает дефицит объема D — у.
Рис. 4

Ожидаемые затраты М{С(у)} на период выражаются следующей формулой.
Можно показать, что функция М{С(у)} является выпуклой по у и, таким образом, имеет единственный минимум. Следовательно, вычисляя первую производную функции М{С(у)} по у и приравнивая ее к нулю, получим
или
Отсюда имеем
Правая часть последней формулы известна как критическое отношение. Значение у* определено только при условии, что критическое отношение неотрицательно, т.е. . Случай, когда , является бессмысленным, так как это предполагает, что стоимость закупки единицы продукции выше потери от неудовлетворенного спроса.

Ранее предполагалось, что спрос D является непрерывной случайной величиной. Если же D является дискретной величиной, то плотность распределения вероятностей f(D) определена лишь в дискретных точках и функция затрат определяется в соответствии с формулой.
Необходимыми условиями оптимальности являются неравенства
М{С(у - 1)} ≥ М{С(у)} и М{С(у + 1)} ≥ М{С(у)}.
Эти условия в данном случае являются достаточными, так как функция М{С(у)} выпукла. Применение этих условий после некоторых алгебраических преобразований приводит к следующим неравенствам для определения у*.

2.2. Модель при наличии затрат на оформление заказа
Данная модель отличается от выше представленной тем, что учитывается стоимость К размещения заказа. Используя обозначения, введенные выше, получаем следующее выражение для суммарной ожидаемой стоимости.
Как показано в разделе 2.1, оптимальное значение y* должно удовлетворять соотношению

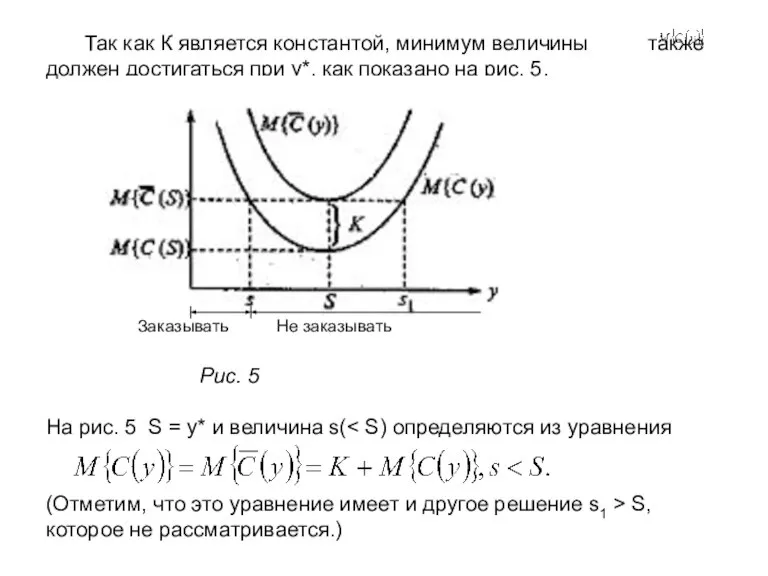
Так как К является константой, минимум величины также должен достигаться при у*, как показано на рис. 5. Заказывать Не заказывать
Рис. 5
На рис. 5 S = y* и величина s(< S) определяются из уравнения
(Отметим, что это уравнение имеет и другое решение s1 > S, которое не рассматривается.)

Задача формулируется следующим образом. Какое количество продукции необходимо заказывать, если наличный запас перед размещением заказа составляет х единиц? Ответ на этот вопрос рассматривается по отдельности при выполнении следующих условий.
1. x
S.
Случай 1 (х < s). Так как в наличии имеется х единиц продукции, соответствующие издержки содержания запаса составляют М{С(х)}. Если заказывается любое дополнительное количество продукции у (у > х), то соответствующие затраты при заданной величине у равны величине М{С(у)}, которая учитывает стоимость К размещения заказа. Из рис. 5 следует, что
Следовательно, оптимальной стратегией управления запасами в этом случае будет заказ в S - х единиц.

Случай 2 (s≤x≤S). Из рис. 5 видно, что
Следовательно, в данном случае дополнительных затрат не возникает, если новый заказ не размещается. Поэтому у* =х.
Случай 3 (х> S). Из рис. 5 видно, что при у > х
Это неравенство показывает, что в данном случае экономнее будет не размещать заказ, т.е. у*=х.
Описанная стратегия управления запасами, часто именуемая (s-S)-стратегией, определяется следующим правилом.
Если х < s, делать заказ объемом S - х,
если х ≥ s, заказывать не следует.
(Оптимальность (s-S)-стратегии следует из того, что соответствующая функция затрат является выпуклой. Если это свойство не выполняется, данная стратегия перестает быть оптимальной.)

3. Многоэтапные модели
Рассматривается многоэтапная модель в предположении, что не учитывается стоимость размещения заказа. Кроме того, в модели предусматривается возможность задолженности и нулевое время поставки. Предполагается также, что спрос D в каждый период описывается стационарной (независящей от времени) плотностью вероятности f(D).
В многоэтапной модели учитывается приведенная стоимость денег. Если α (< 1) – коэффициент дисконтирования (процент скидки) для одного этапа, то сумма А спустя n этапов будет эквивалентна сумме α n А в настоящий момент.
Предположим, что горизонт планирования охватывает n этапов и неудовлетворенный спрос может оставаться таковым лишь на протяжении одного этапа. Пусть Fi(xi) — максимальная суммарная ожидаемая прибыль для этапов от i до n, определенная при условии, что хi — уровень имеющегося запаса перед размещением заказа на i-м этапе.

Используя обозначения из раздела 2 и предполагая, что r — удельный доход от реализации единицы продукции, сформулируем задачу управления запасами в виде следующей задачи динамического программирования.
где F n+1 (yn-D) ≡ 0. Величина xi может принимать отрицательные значения, так как неудовлетворенный спрос может накапливаться. Величина αr(D-yi) включена во второй интеграл, поскольку D-yi представляет собой неудовлетворенный спрос на i-м этапе, который должен быть удовлетворен на этапе i+1 .

Задачу можно решить рекуррентно методами динамического программирования. Если число этапов является бесконечным (бесконечный горизонт планирования), приведенное выше рекуррентное уравнение сводится к следующему.
где х и у представляют собой уровни запаса на каждом этапе до и после получения заказа соответственно.
Оптимальное значение у можно определить из приведенного ниже необходимого условия, которое в данном случае есть также достаточным, так как функция ожидаемой прибыли F(x) является вогнутой.

Величина
определяется следующим образом. Если на начало следующего этапа уровень запаса еще составляет β (> 0) единиц, то прибыль на этом этапе возрастает на величину cβ, так как объем последующего заказа уменьшается именно на эту величину. Это означает, что
Следовательно, необходимое условие принимает вид
Поэтому оптимальный уровень заказа у* определяется из уравнения
Оптимальная стратегия каждого этапа при заданном исходном запасе х выражается следующим правилом.
Если х < у*, делать заказ объемом у* - х,
если х ≥ у*, заказа не делать.

4. Заключение
В моделях управления запасами спрос является случайным. Предложен широкий спектр методов решения построенных моделей — от вероятностной (рандомизированной) версии детерминированной модели экономичного размера заказа до более сложных, связанных с применением методов динамического программирования.
Литература
Хедли Дж., Уайтин Т. Анализ систем управления запасами.— М: Наука, 1969.)
Кофман А. Методы и модели исследования операций. — М.: Мир, 1966.

Основные соотношения СМО
В теории МО обычно рассматривается один параметр – время. Базовый случайный процесс – пуассоновский.
Распределение Пуассона ,
где Pn(t) – вероятность того, что за промежуток t поступит n требований.
Свойства:
е-λt - вероятность отсутствия требований в интервале t;
λt(e-λt) - вероятность поступления одного требования за время t;
следовательно вероятность поступления за время t более одного требования
т.е. функция, которая ведет себя как t2.
Отсюда следует, что при малых t, все члены с t2 - пренебрежимо малы.
При малых t вероятность наступления более одного требования пренебрежимо мала

Рассмотрим стационарный режим. Понятие стационарного состояния классически поясняется в решении двух задач МО:
- модель Эрланга (изменение Pn(t) в зависимости от t описывается Pn/(t), т.е. Pn/(t) = 0);
- формула Поллачека- Хинчина (из рассмотрения , что также приводит к Pn(t), не зависящим от t.
(1) - исходные выражения для
пуассоновского распределения

Модель Эрланга
Допущения:
-процесс начинается при отсутствии требований в очереди;
- СМО с пуассоновским входящим потоком с параметром λ;
- экспоненциальное время обслуживания с параметром μ;
- дисциплина очереди FIFO.
Исходные уравнения
Замечание: член, содержащий (∆t)2 опускается. Поэтому, например, выражение (1-λ∆t)(1-μ∆t) (за время ∆t в систему не поступит и не покинет ни одно требование) преобразуется в 1-(λ+μ)∆t.
(2)

Перенесем Pn(t) в левую часть и при ∆t→0 имеем
Исследуем стационарное состояние, приравняв производные по времени к нулю.
Введем понятие загрузки системы α = λ/μ.
Если λ/μ ≥1, то число ожидающих требований растет неограниченно и стационарный режим не устанавливается .
Для стационарного состояния при λ/μ <1 найдем выражения для :
- математического ожидания числа требований, находящихся в очереди;
- среднего времени ожидания.
(3)

Приравняв к нулю производные в (3), получим:
Учитывая, что α=λ/μ преобразуем (4)
Пусть в первом уравнении системы (5) n=1. Тогда (1+α)P1=P2+αP0 и, учитывая, что P1=αP0, имеем P2=α2P0.
Повторяя этот процесс, получаем Pn=αnP0. (6)
Напомним, что , поэтому или
, откуда P0=1-α и Pn= αn(1-α) (7)
Выражение (7) представляет собой геометрическое распределение.
(4)
(5)

Математическое ожидание (L) числа требований, находящихся в системе (с учетом (7))
Математическое ожидание числа требований, находящихся в очереди
(8)
(9)

Формула Поллачека-Хинчина
Рассматривается одноканальная СМО, находящаяся в стационарном режиме с входным пуассоновским случайным процессом с параметром λ.
Время обслуживания имеет произвольное распределение с интенсивностью μ клиентов в ед. времени. Дисциплина очереди FIFO.
Анализируем стационарный режим при λ/μ < 1; t→∞.
q/ = max (q-1,0)+r = q-1+δ+r, δ(q)=
«δ» вводится, чтобы не использовать символ max.
остается q
клиентов
q-1
время
t – время
обслуживания
клиентов
моменты времени,
когда обслуженные
клиенты попадают
в систему и начало
обслуживания новых
0, если q>0
1, если q=1
↑ r клиентов поступает в систему