Содержание
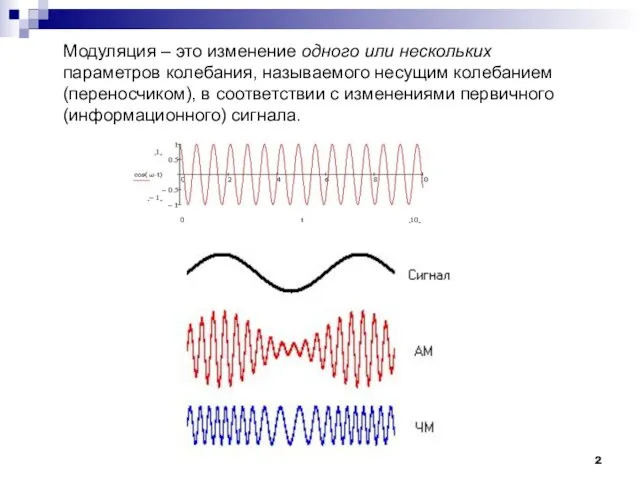
- 2. Модуляция – это изменение одного или нескольких параметров колебания, называемого несущим колебанием (переносчиком), в соответствии с
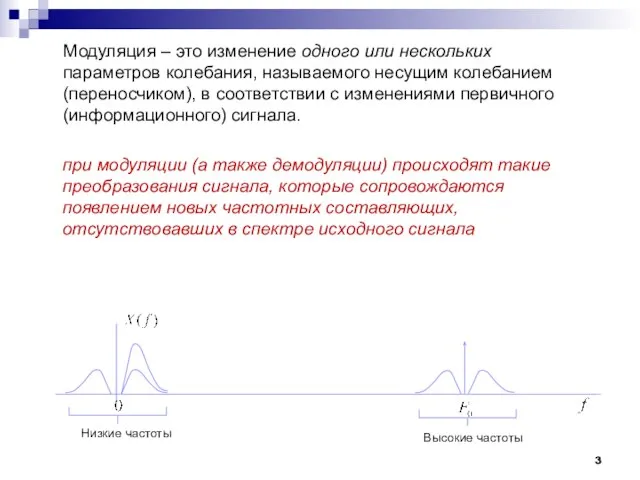
- 3. Модуляция – это изменение одного или нескольких параметров колебания, называемого несущим колебанием (переносчиком), в соответствии с
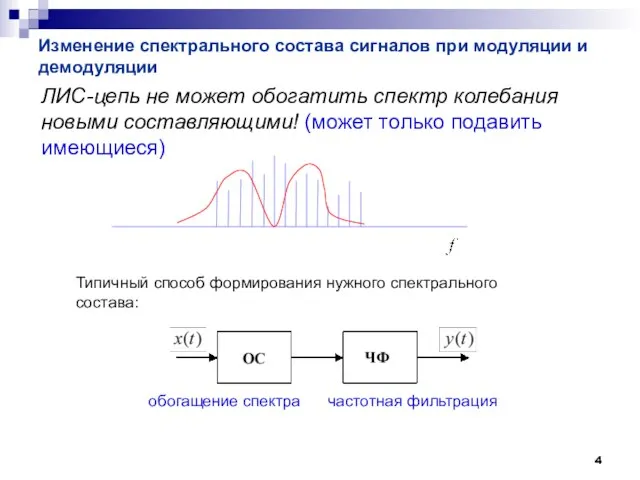
- 4. Изменение спектрального состава сигналов при модуляции и демодуляции ЛИС-цепь не может обогатить спектр колебания новыми составляющими!
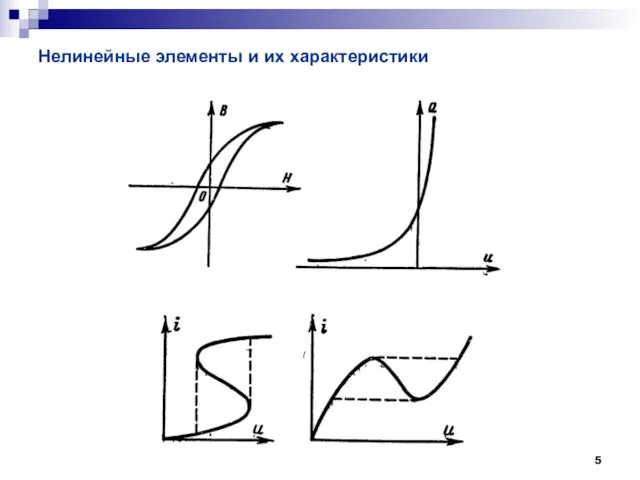
- 5. Нелинейные элементы и их характеристики
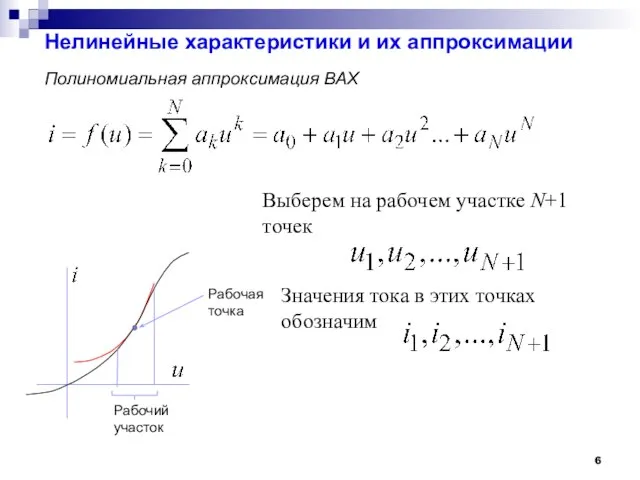
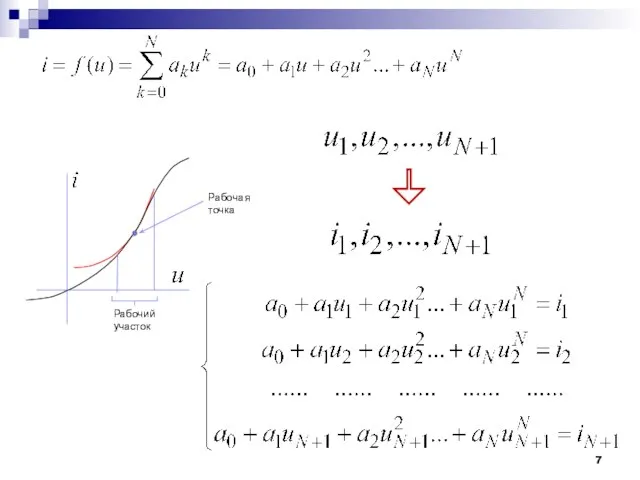
- 6. Нелинейные характеристики и их аппроксимации Рабочая точка Рабочий участок Выберем на рабочем участке N+1 точек Значения
- 7. Рабочая точка Рабочий участок
- 8. Аппроксимация методом наименьших квадратов МНК:
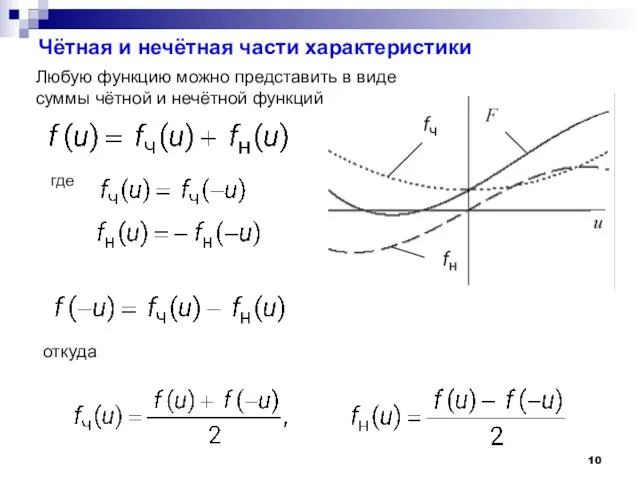
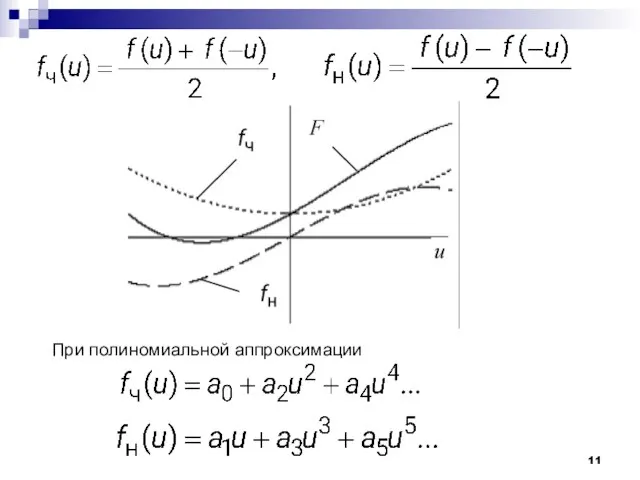
- 10. Чётная и нечётная части характеристики Любую функцию можно представить в виде суммы чётной и нечётной функций
- 11. При полиномиальной аппроксимации
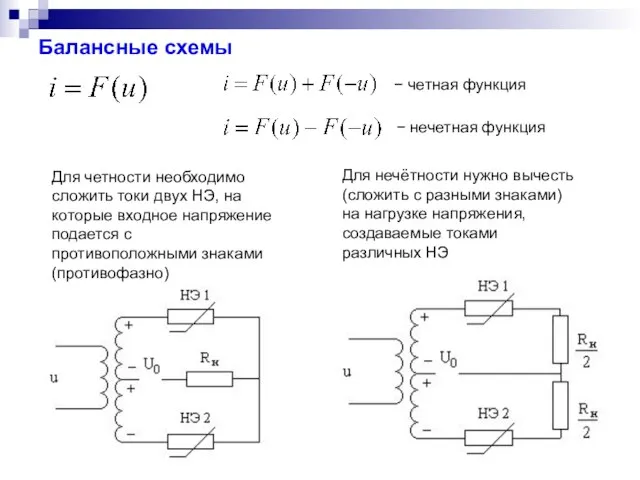
- 12. Балансные схемы − четная функция − нечетная функция Для четности необходимо сложить токи двух НЭ, на
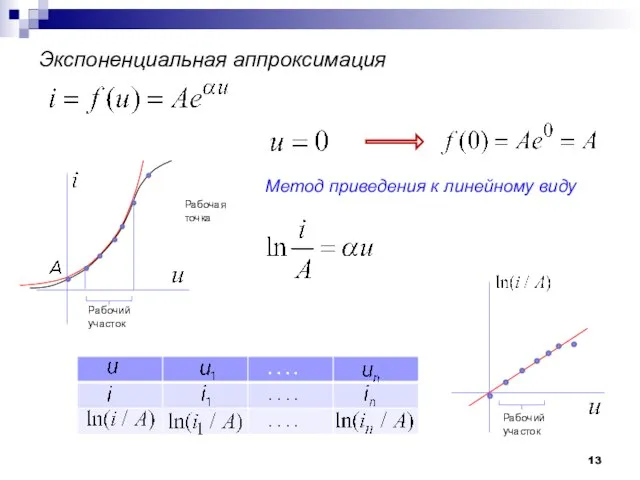
- 13. Экспоненциальная аппроксимация Рабочая точка Рабочий участок Метод приведения к линейному виду Рабочий участок
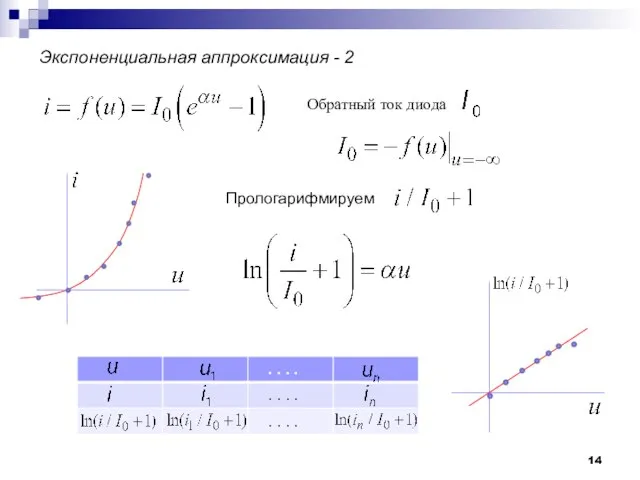
- 14. Экспоненциальная аппроксимация - 2 Обратный ток диода Прологарифмируем
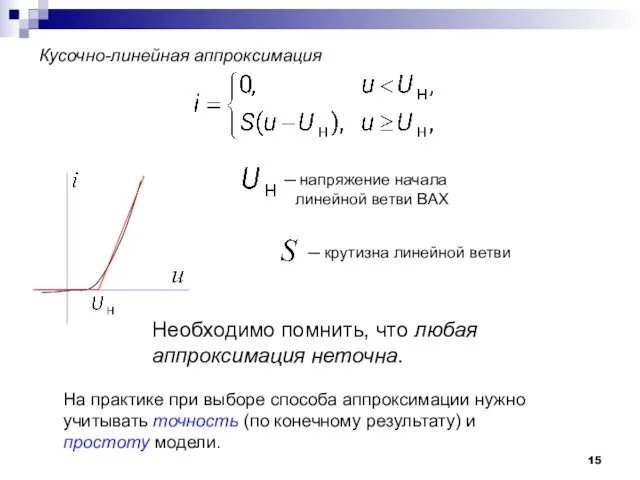
- 15. Кусочно-линейная аппроксимация напряжение начала линейной ветви ВАХ На практике при выборе способа аппроксимации нужно учитывать точность
- 16. Воздействие гармонического колебания на нелинейный элемент − напряжение смещения для выбора р.т. кратные гармоники
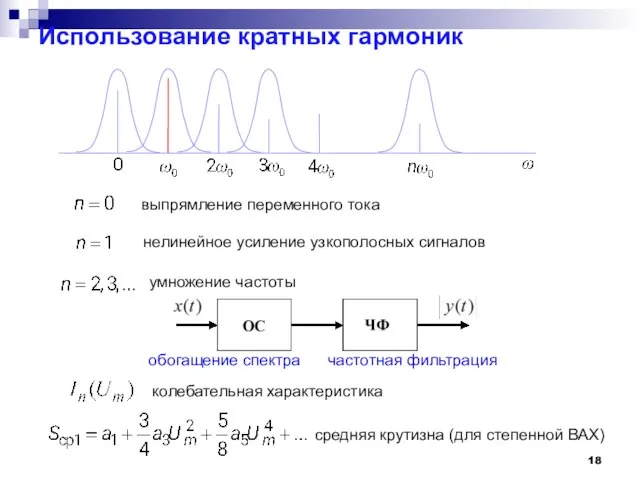
- 18. Использование кратных гармоник выпрямление переменного тока нелинейное усиление узкополосных сигналов обогащение спектра частотная фильтрация умножение частоты
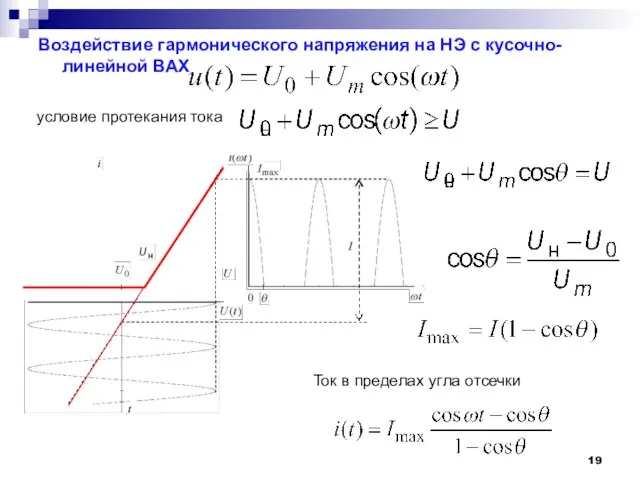
- 19. Воздействие гармонического напряжения на НЭ с кусочно-линейной ВАХ условие протекания тока Ток в пределах угла отсечки
- 20. разлагаем в ряд Фурье Коэффициенты ряда
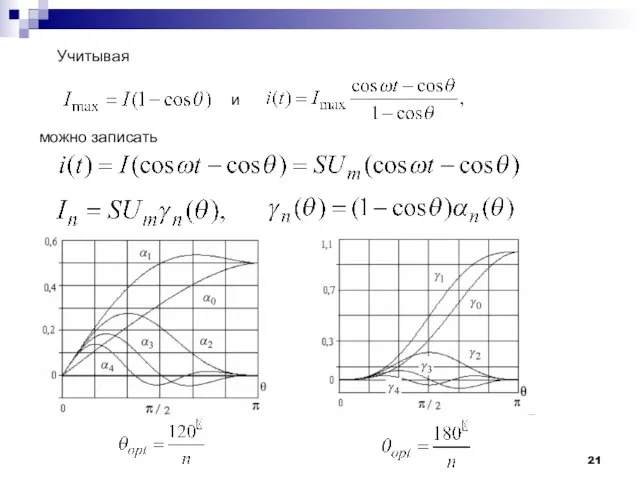
- 21. Учитывая и можно записать
- 22. Бигармоническое воздействие на НЭ При возведении суммы гармонических составляющих в целые степени будут получаться произведения согласно
- 23. Например, если полином имеет степень 2, в спектре тока будут частоты Если полином имеет степень 3,
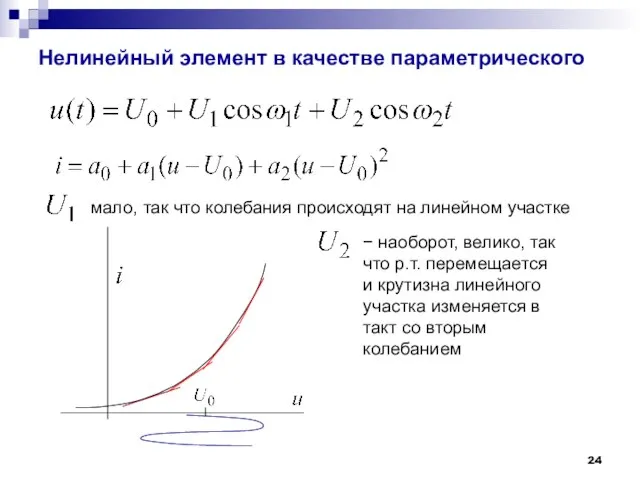
- 24. Нелинейный элемент в качестве параметрического − наоборот, велико, так что р.т. перемещается и крутизна линейного участка
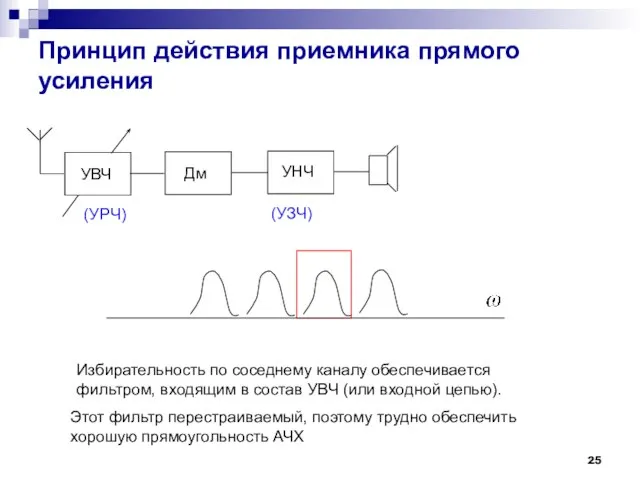
- 25. Принцип действия приемника прямого усиления УВЧ Дм УНЧ Избирательность по соседнему каналу обеспечивается фильтром, входящим в
- 26. Принцип действия супергетеродинного приемника Узкополосный ВЧ-сигнал слабый Крутизна ПЧ (См) изменяется по закону УВЧ ПЧ Гет
- 28. Скачать презентацию








 Diagnostirovanie_i_TO_transmissii
Diagnostirovanie_i_TO_transmissii Основные характеристики гребных винтов
Основные характеристики гребных винтов Техническая механика. Раздел: Теоретическая механика. Лекция 1
Техническая механика. Раздел: Теоретическая механика. Лекция 1 Механические волны
Механические волны Зенкерование и развертывание отверстий
Зенкерование и развертывание отверстий Сверхпроводимость. Эффект Мейсснера
Сверхпроводимость. Эффект Мейсснера Кинематика. Равномерное прямолинейное движение
Кинематика. Равномерное прямолинейное движение Топливный бак. Назначение, устройство
Топливный бак. Назначение, устройство Теория кварков
Теория кварков Методы наблюдения и регистрации элементарных частиц
Методы наблюдения и регистрации элементарных частиц Первый закон термодинамики
Первый закон термодинамики Физика и технология наноструктур
Физика и технология наноструктур Законы Ньютона. Введение в космодинамику
Законы Ньютона. Введение в космодинамику Ядерный реактор
Ядерный реактор Аксиомы динамики
Аксиомы динамики Нагревание проводников электрическим током. Закон Джоуля – Ленца. 8 класс
Нагревание проводников электрическим током. Закон Джоуля – Ленца. 8 класс Ракетный двигатель. Импульс тела
Ракетный двигатель. Импульс тела Импульс тела. Закон сохранения импульса
Импульс тела. Закон сохранения импульса Нобелевская премия. Физика и религия. Высшая цель физика
Нобелевская премия. Физика и религия. Высшая цель физика Строительный экскаватор. Гидравлический цилиндр
Строительный экскаватор. Гидравлический цилиндр Элементы машиноведения. Составные части машин
Элементы машиноведения. Составные части машин Строение атомов химических элементов
Строение атомов химических элементов Презентация на тему Шкала электромагнитных излучений
Презентация на тему Шкала электромагнитных излучений  Магнитное поле Земли 8 класс - Презентация
Магнитное поле Земли 8 класс - Презентация Презентация на тему Взаимодействие тел
Презентация на тему Взаимодействие тел  Современное состояние прецизионной кварцевой стабилизации частоты применительно к задачам частотно-временного обеспечения
Современное состояние прецизионной кварцевой стабилизации частоты применительно к задачам частотно-временного обеспечения Буровые машины для открытых горных пород. Лекция 8
Буровые машины для открытых горных пород. Лекция 8 Газораспределительный механизм
Газораспределительный механизм