Содержание
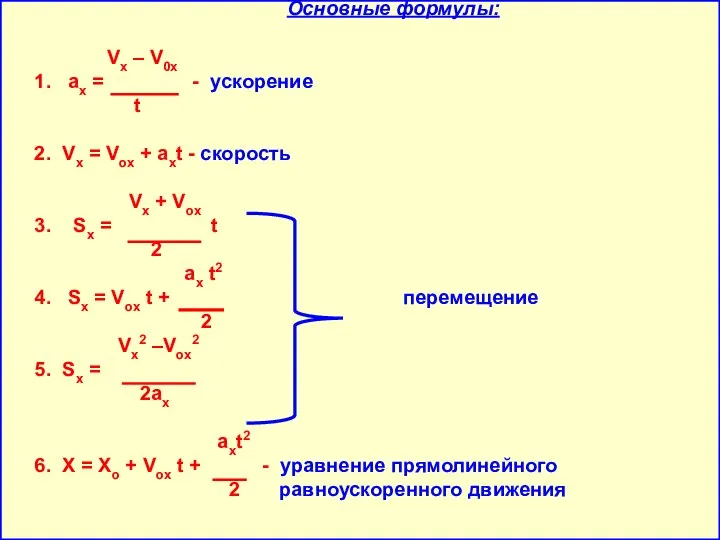
- 2. Основные формулы: Vx – V0x 1. аx = - ускорение t 2. Vx = Vox +
- 3. Задача №1. С каким ускорением движется гоночный автомобиль, если его скорость за 6 с увеличивается со
- 4. Задача №1. С каким ускорением движется гоночный автомобиль, если его скорость за 6 с увеличивается со
- 5. Задача №2 За какое время ракета приобретает первую космическую скорость 7,9 км/с, если она будет двигаться
- 6. Задача №2 За какое время ракета приобретает первую космическую скорость 7,9 км/с, если она будет двигаться
- 7. Задача №3 Рассчитайте длину взлетной полосы, если скорость самолета 300 км/ч, а время разгона 40 с.
- 8. Задача №3 Рассчитайте длину взлетной полосы, если скорость самолета 300 км/ч, а время разгона 40 с.
- 9. Задача №4 Скорость гоночного автомобиля в момент начала разгона 10 м/с, ускорение 5 м/с2. Определите путь,
- 10. Задача №4 Скорость гоночного автомобиля в момент начала разгона 10 м/с, ускорение 5 м/с2. Определите путь,
- 11. Задача №5 Тормозной путь автомобиля, движущегося со скоростью 50 км/ч, равен 10 м. Чему равен тормозной
- 12. Задача №5 Тормозной путь автомобиля, движущегося со скоростью 50 км/ч, равен 10 м. Чему равен тормозной
- 13. Задача №6 Какова длинна пробега самолета при посадке, если его посадочная скорость 140 км/ч, а ускорение
- 14. Задача №6 Какова длинна пробега самолета при посадке, если его посадочная скорость 140 км/ч, а ускорение
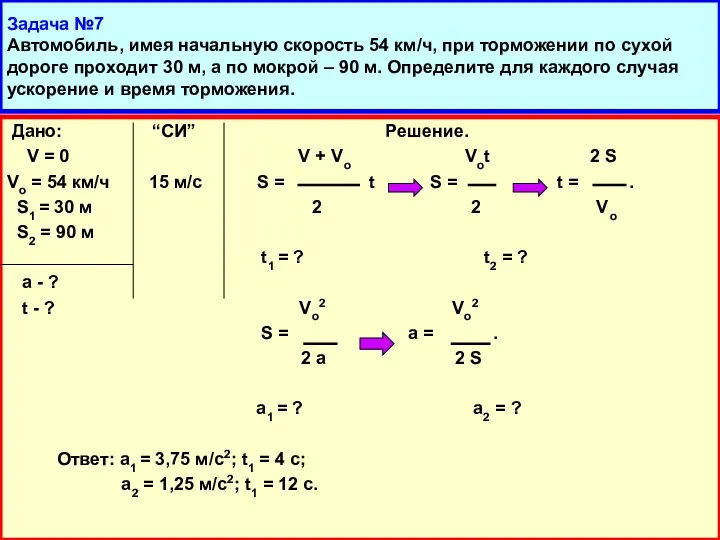
- 15. Задача №7 Автомобиль, имея начальную скорость 54 км/ч, при торможении по сухой дороге проходит 30 м,
- 16. Задача №7 Автомобиль, имея начальную скорость 54 км/ч, при торможении по сухой дороге проходит 30 м,
- 17. Задача №8 При равноускоренном движении с начальной скоростью 5 м/с тело за 3 с прошло 20
- 18. Задача №8 При равноускоренном движении с начальной скоростью 5 м/с тело за 3 с прошло 20
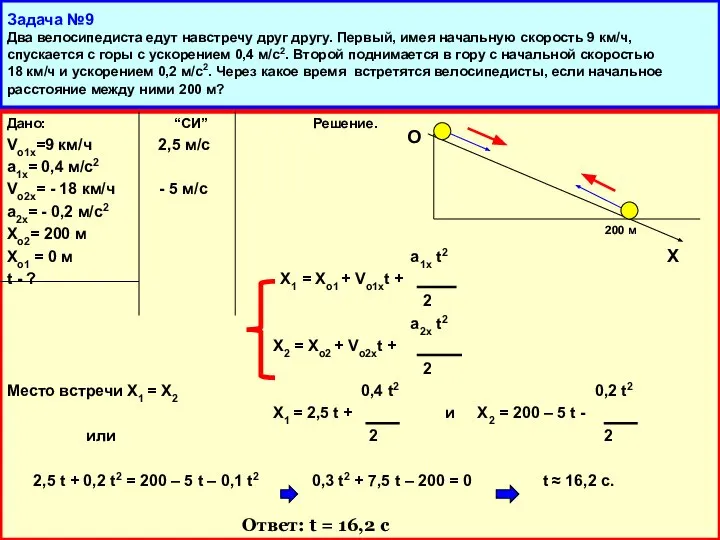
- 19. Задача №9 Два велосипедиста едут навстречу друг другу. Первый, имея начальную скорость 9 км/ч, спускается с
- 20. Задача №9 Два велосипедиста едут навстречу друг другу. Первый, имея начальную скорость 9 км/ч, спускается с
- 21. Задача №10 Уравнение координаты имеет вид Х = 4 + 1,5t + t2. Какое это движение?
- 23. Скачать презентацию

















 Электроника и микропроцессорная техника
Электроника и микропроцессорная техника Условия плавания тел
Условия плавания тел Расчет статических нагрузок тела под собственным весом
Расчет статических нагрузок тела под собственным весом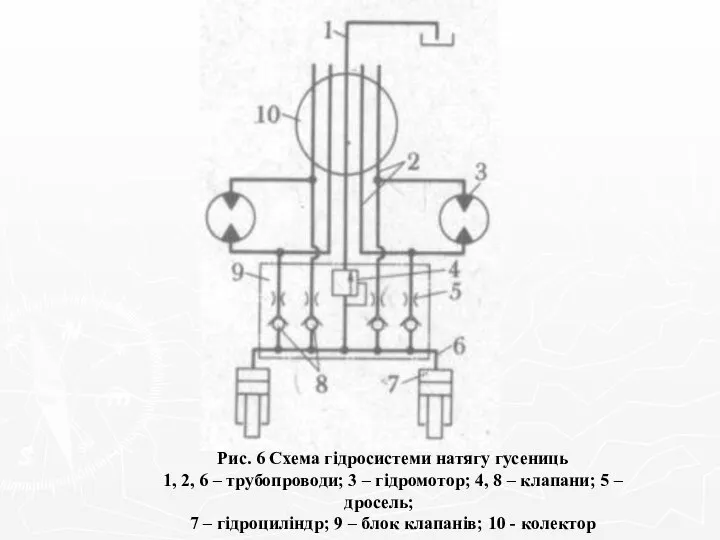 Схема гідросистеми натягу гусениць
Схема гідросистеми натягу гусениць Газообразное состояние
Газообразное состояние Применение ядерной энергии: проблемы и перспективы
Применение ядерной энергии: проблемы и перспективы Виды движения по форме траектории
Виды движения по форме траектории Энергия топлива
Энергия топлива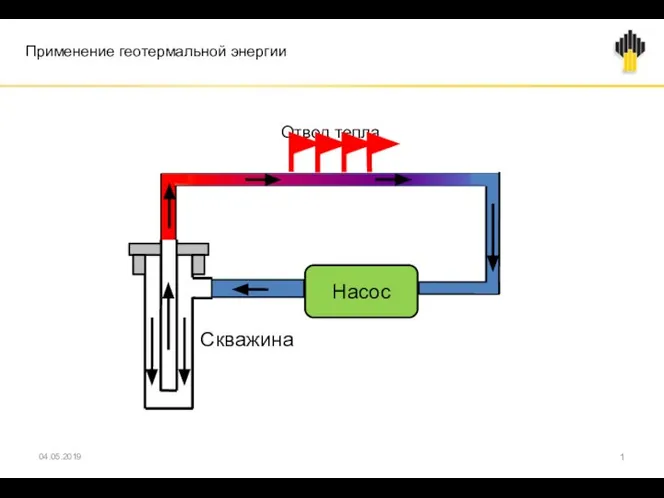 Применение геотермальной энергии
Применение геотермальной энергии Судовые двигатели внутреннего сгорания. Лекция 17
Судовые двигатели внутреннего сгорания. Лекция 17 Расчет бункеров
Расчет бункеров Монтаж оптических кабелей
Монтаж оптических кабелей Станция Физический калейдоскоп
Станция Физический калейдоскоп Ядерные реакции и их воздействия
Ядерные реакции и их воздействия Магнитное поле в веществе. Закон полного тока. Граничные условия
Магнитное поле в веществе. Закон полного тока. Граничные условия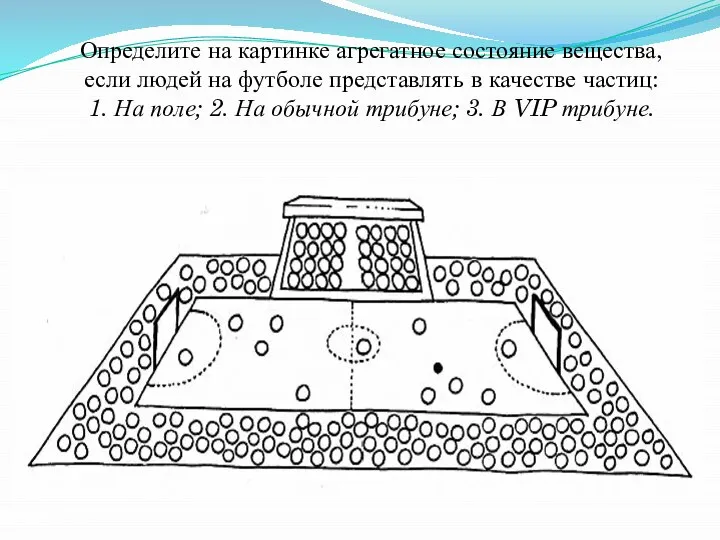 Физические свойства вещества: текучесть, плотность, тепло и электропроводность, ковкость и пластичность
Физические свойства вещества: текучесть, плотность, тепло и электропроводность, ковкость и пластичность Правила и приёмы решения задач
Правила и приёмы решения задач Направление тока и направление линий его магнитного поля
Направление тока и направление линий его магнитного поля Тепловые двигатели
Тепловые двигатели Ионное испарение. Механизм распыления при ионном испарении. Катодное испарение: диодное, диодное со смещением и триодное
Ионное испарение. Механизм распыления при ионном испарении. Катодное испарение: диодное, диодное со смещением и триодное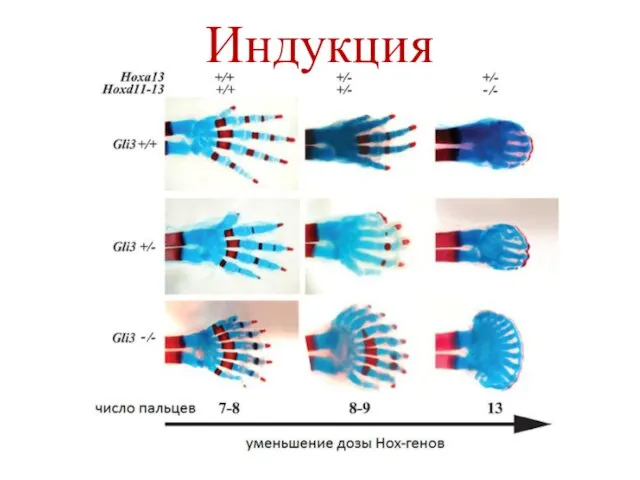 Индукция
Индукция Трение - полезное или вредное явление?
Трение - полезное или вредное явление? Презентация на тему Магнитное поле и его графическое изображение
Презентация на тему Магнитное поле и его графическое изображение  Лекция 23. Оптика. Волновая оптика
Лекция 23. Оптика. Волновая оптика Характеристики неявного метода и основные пути решения. Программный комплекс LS-Dyna
Характеристики неявного метода и основные пути решения. Программный комплекс LS-Dyna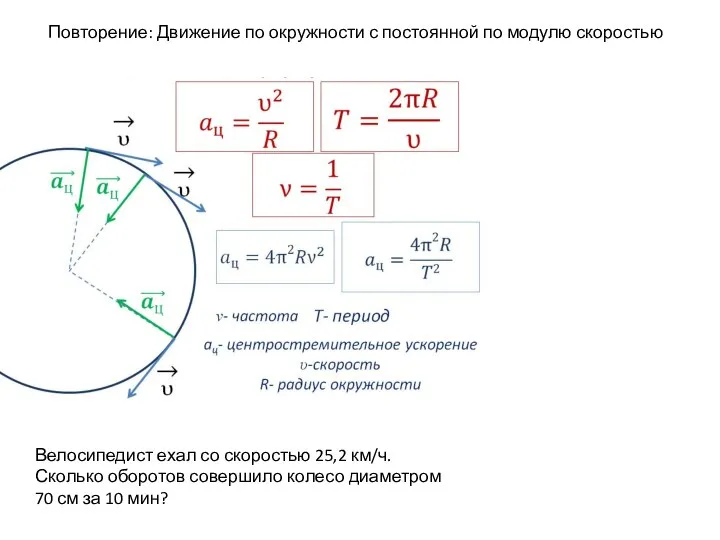 Закон всемирного тяготения
Закон всемирного тяготения Презентация на тему Механика Ньютона
Презентация на тему Механика Ньютона  Законы Ньютона
Законы Ньютона