Слайд 2Аннотация
В данном практическом занятии изучены теоретические основы контактно взаимодействия на которых

основывается в своих расчетах программный комплекс LS-Dyna. Рассмотрены характеристики неявного метода и основные пути решения.
Слайд 3План практического занятия
Характеристика неявного метода
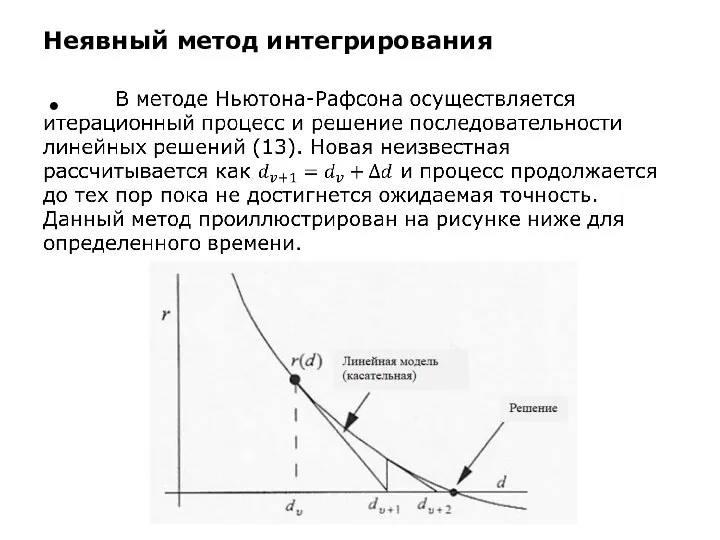
Неявный метод интегрирования
Метод Ньютона для расчета

n неизвестных
Пример. Одномерная нелинейная пружина
Линейная динамика неявного метода
Статический нелинейный неявный метод
Статический линейный неявный метод
Слайд 4Характеристика неявного метода
Производится вычисление глобальной матрицы жесткости, инверсия матрицы (нахождение обратной матрицы),

после чего к узлам прикладывается разуравновешивающая сила для получения приращения перемещения. Достоинство такого подхода заключается в том, что пользователь может сам задать величину временного шага. Недостатком является большая сложность формирования, хранения, разложения на множители матрицы жесткости. Поэтому задачи с неявным решением обычно включают сравнительно небольшое число временных шагов интегрирования.
Слайд 5Характеристика неявного метода

Слайд 6Характеристика неявного метода

Слайд 7Неявный метод интегрирования

Слайд 8Неявный метод интегрирования

Слайд 9Неявный метод интегрирования

Слайд 12Метод Ньютона для расчета n неизвестных

Слайд 13Метод Ньютона для расчета n неизвестных
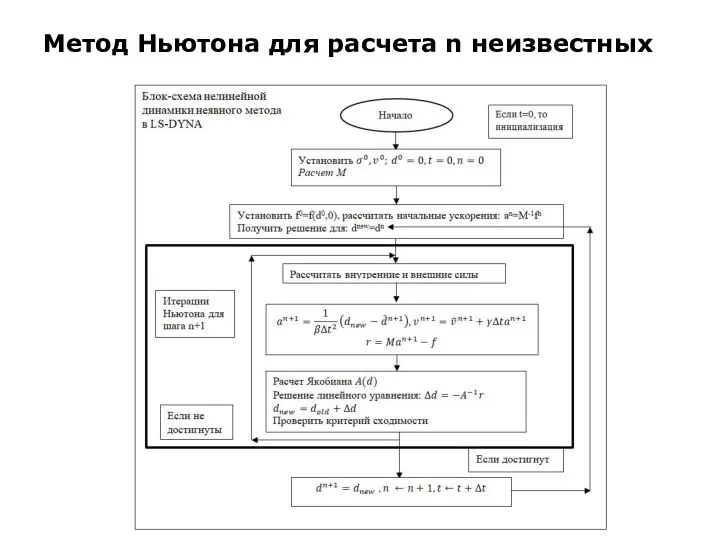
Слайд 14Метод Ньютона для расчета n неизвестных
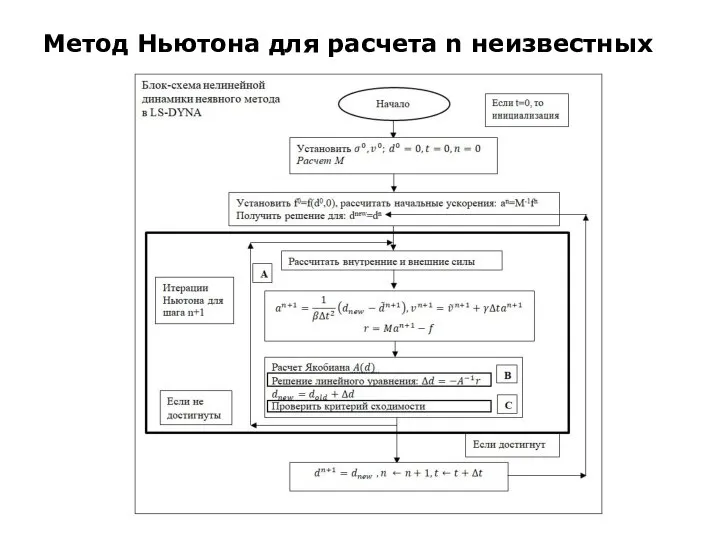
Слайд 15Метод Ньютона для расчета n неизвестных
Ниже более детально описываются три аспекта, отраженные

в блок-схеме:
A: Для решения уравнений равновесия используются итерационные методы. В данном пособии рассматривался метод Ньютона-Рафсона, хотя пользователь может выбрать любой другой метод, встроенный в программный комплекс LS-DYNA. Сделать это можно через карточку *CONTROL_IMPLICIT_SOLUTION, где также задаются параметры итерационного процесса. Более подробно эти методы рассмотрены в разделе Implicit in LS-DYNA.
B: Для нахождения Δd решается линейное уравнение, при этом матрица A инвертируется (находится обратная матрица). Выбрать решатель для этой задачи можно с помощью карточки *CONTROL_IMPLICIT_SOLVER.
C: Производится проверка критерия сходимости. В LS-DYNA существует три критерия. В карточке *CONTROL_IMPLICIT_SOLUTION можно задать критерий и другие параметры. Далее эти критерии рассмотрены более подробно. Настройки управления можно найти в разделе Implicit in LS-DYNA.
Слайд 16Метод Ньютона для расчета n неизвестных

Слайд 17Метод Ньютона для расчета n неизвестных
Видно, что, если внешняя нагрузка не изменяется

после предыдущего шага, то величина невязки r будет изначально равна нулю. Это вызовет проблемы для энергетического критерия, поскольку знаменатель обратится в ноль. В этом случае LS-DYNA отображает критерий энергии 1,000. Рекомендуется применять нагрузку, которая меняется на каждом шаге.
Слайд 18Метод Ньютона для расчета n неизвестных

Слайд 19Метод Ньютона для расчета n неизвестных
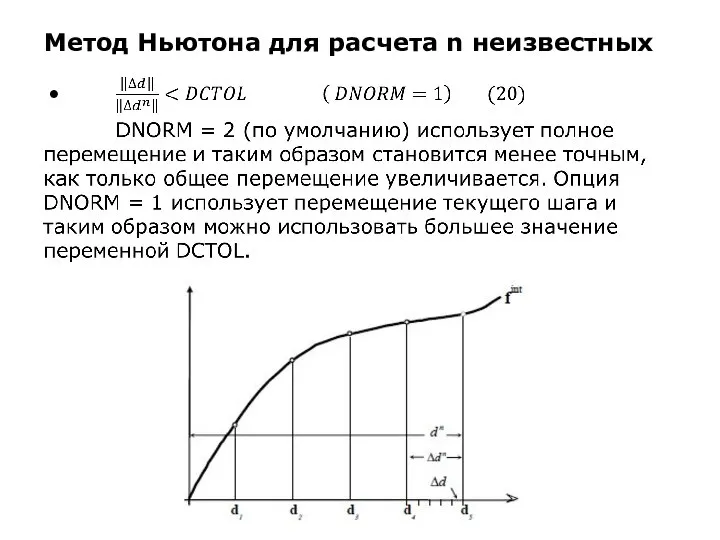
Слайд 20Пример. Одномерная нелинейная пружина
Для того, что проиллюстрировать метод Ньютона, рассмотрим простую нелинейную
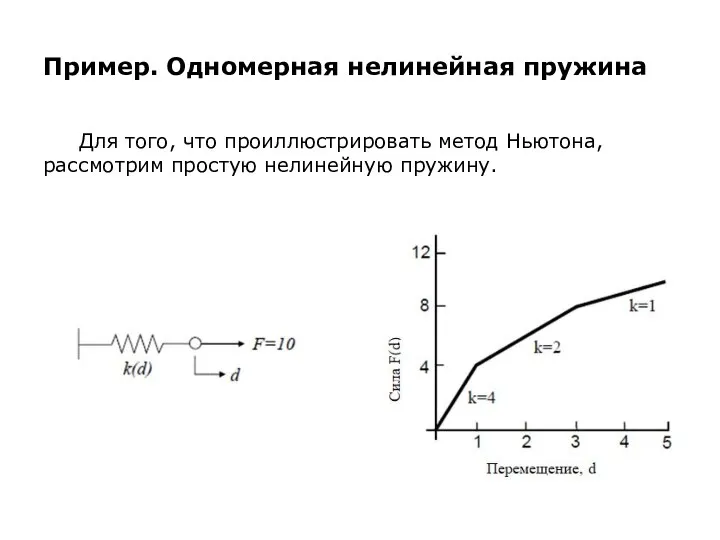
пружину.
Слайд 21Пример. Одномерная нелинейная пружина

Слайд 22Пример. Одномерная нелинейная пружина
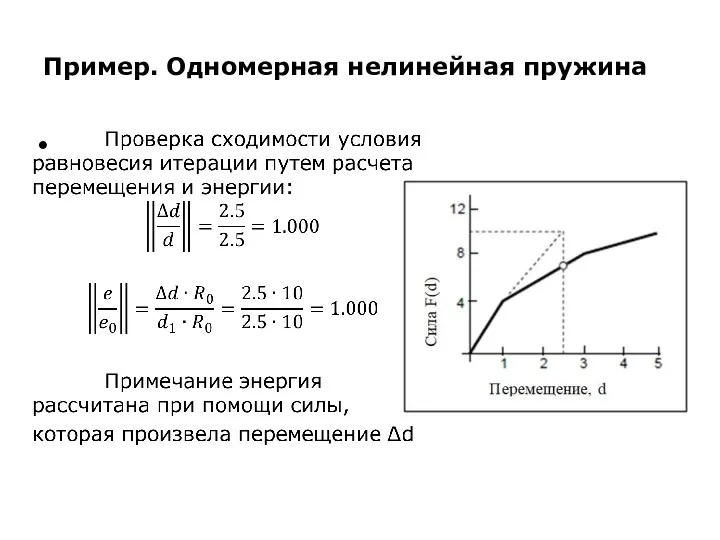
Слайд 23Пример. Одномерная нелинейная пружина
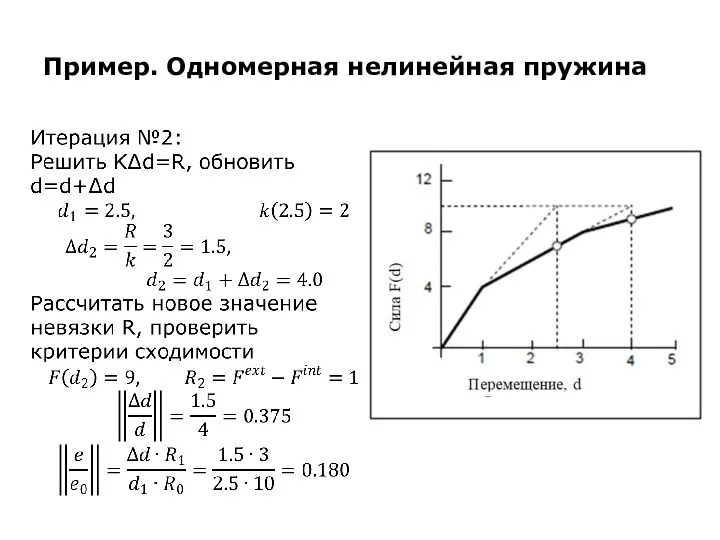
Слайд 24Пример. Одномерная нелинейная пружина
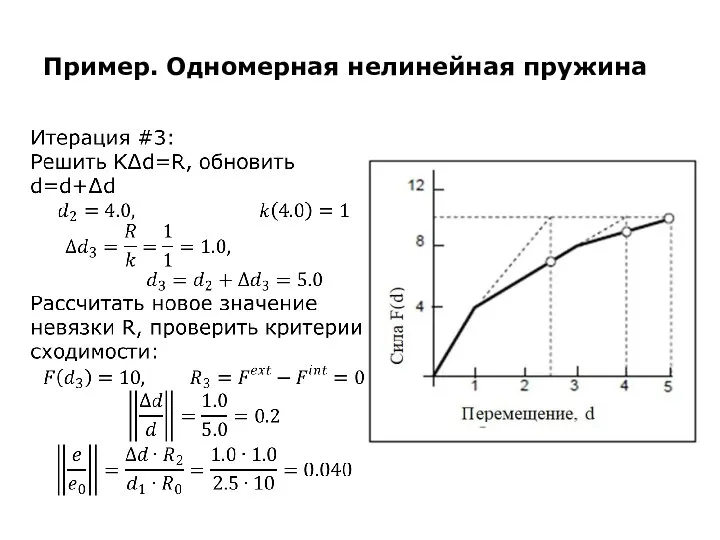
Слайд 25Пример. Одномерная нелинейная пружина

Слайд 26Пример. Одномерная нелинейная пружина

Слайд 27Линейная динамика неявного метода
Ранее была показана нелинейная динамика, но иногда модель

может быть рассчитана как линейная. Это значит, что деформация, материалы и т.д. линейно зависимы. Как задать линейный анализ в LS-DYNA показано в разделах Activate the Implicit Solver и Implicit in LS- DYNA. Ниже дана блок-схема. Стоит запомнить одну вещь, что если задан любой вид контакта в задаче, то это превращает модель в нелинейную.
Слайд 28Линейная динамика неявного метода
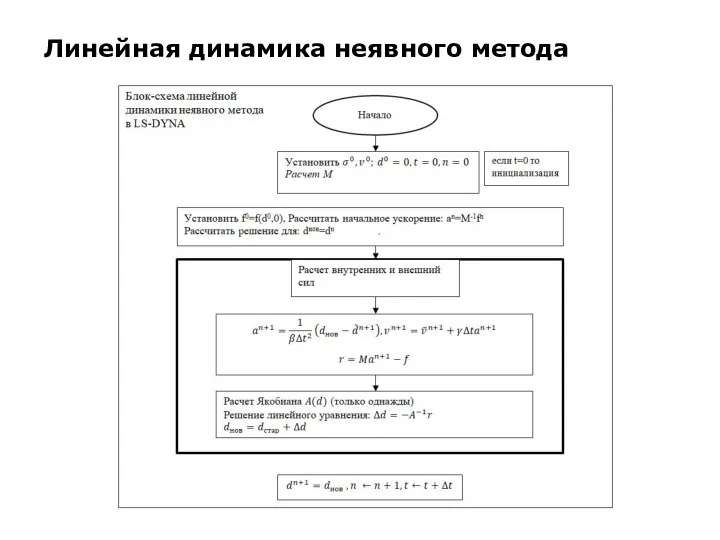
Слайд 29Статический нелинейный неявный метод
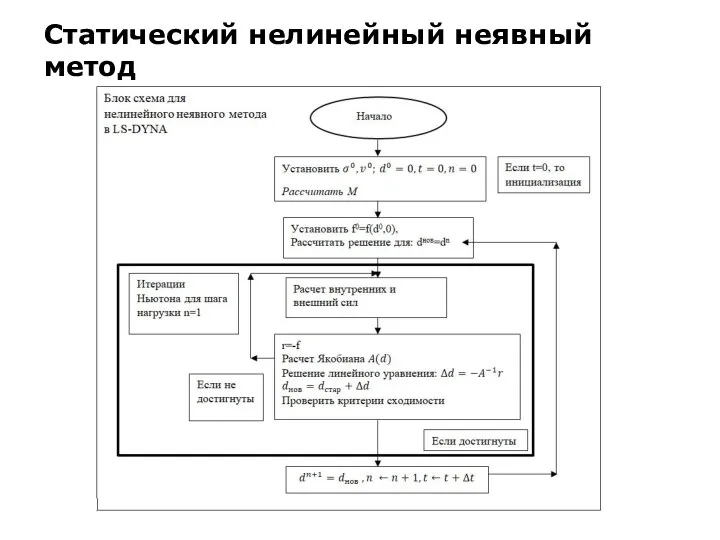
Некоторые расчетный модели могут считаться статическими, уравнение (4) не

учитывая массу (δ=0). Блок схема для статического нелинейного неявного метода показана на рисунке ниже. Статический расчет установлен по умолчанию в LS-DYNA, можно изменить в карточке *CONTROL_IMPLICIT_DYNAMICS.
Слайд 30Статический нелинейный неявный метод




























 Давление жидкости и газа. Закон Паскаля
Давление жидкости и газа. Закон Паскаля Разработка технологии и организация работ по текущему ремонту тормозной системы автобуса ПАЗ-32054
Разработка технологии и организация работ по текущему ремонту тормозной системы автобуса ПАЗ-32054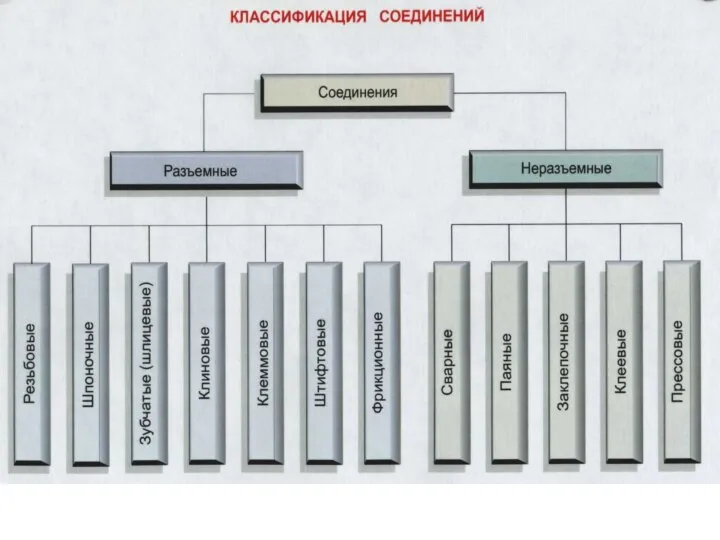 Классификация соединений
Классификация соединений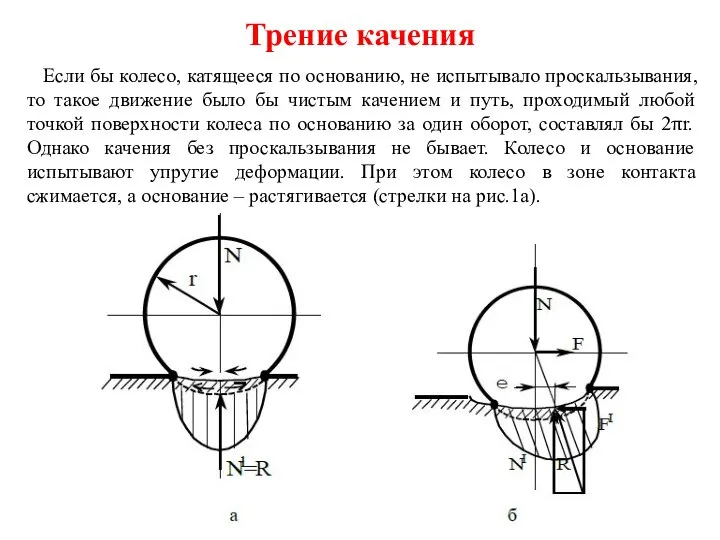 Трение качения
Трение качения Измерение мощности
Измерение мощности Возможна ли машина времени
Возможна ли машина времени Выпускная квалификационная работа: Проектирование шиномонтажного участка АТП
Выпускная квалификационная работа: Проектирование шиномонтажного участка АТП Равномерное движение
Равномерное движение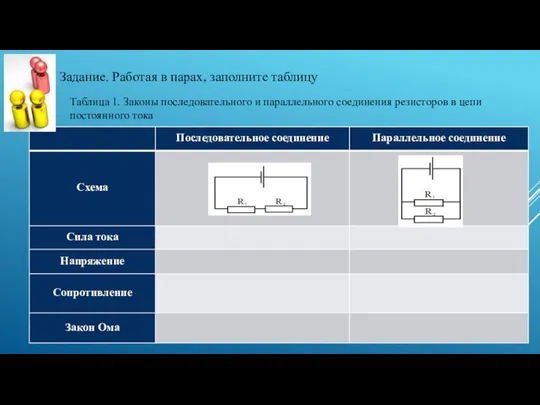 Закон Ома для последовательной электрической цепи переменного тока, содержащей активное и реактивное сопротивления
Закон Ома для последовательной электрической цепи переменного тока, содержащей активное и реактивное сопротивления Постоянные магниты. Магнитное поле Земли
Постоянные магниты. Магнитное поле Земли Достижения современной физики в нашей жизни. Производные предлоги. Узкоспециальные термины. Глаголы с абстрактным значением
Достижения современной физики в нашей жизни. Производные предлоги. Узкоспециальные термины. Глаголы с абстрактным значением Конвекция. Примеры конвекции
Конвекция. Примеры конвекции Типология современного урока (ФГОС)
Типология современного урока (ФГОС) Klassifikatsia_dvigateley_vnutrennego_sgorania
Klassifikatsia_dvigateley_vnutrennego_sgorania Оптика. Уравнения Максвелла. (Лекция 1)
Оптика. Уравнения Максвелла. (Лекция 1) Механическая работа. Мощность
Механическая работа. Мощность Элементы теории относительности
Элементы теории относительности Презентация на тему Движение тел по наклонной плоскости
Презентация на тему Движение тел по наклонной плоскости  Свободные и вынужденные электромагнитные колебания
Свободные и вынужденные электромагнитные колебания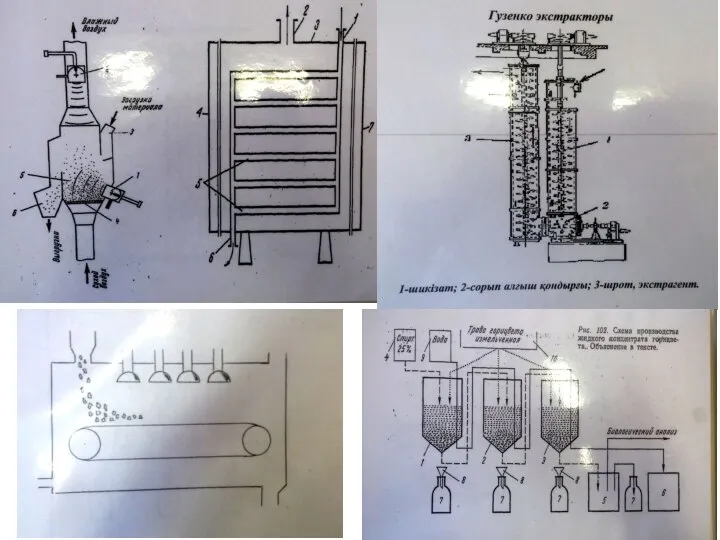 Эстракторы. Схемы
Эстракторы. Схемы Снежные причуды. Всё о снеге и снежинках
Снежные причуды. Всё о снеге и снежинках Оценка одновременно нескольких параметров
Оценка одновременно нескольких параметров Условия равновесия твердых тел
Условия равновесия твердых тел Звуковые волны
Звуковые волны Презентация на тему Основы динамики
Презентация на тему Основы динамики  Исследование эксплуатационных характеристик энергетической установки с ДВС 2Ч 8,5х11 при работе в газодизельном цикле
Исследование эксплуатационных характеристик энергетической установки с ДВС 2Ч 8,5х11 при работе в газодизельном цикле Презентация на тему Энергия связи атомных ядер
Презентация на тему Энергия связи атомных ядер  Влияние электромагнитных волн на организм человека
Влияние электромагнитных волн на организм человека