Содержание
- 2. 1. Геометрические характеристики поперечных сечений Сопротивление бруса внешним силам зависит не только от его размеров и
- 3. Геометрические характеристики Простейшие виды поперечных сечений: A = b·h A = ½ b·h A = πd2/4
- 4. Геометрические характеристики 1.2. Статические моменты поперечного сечения – Sx , Sy . c . C dA
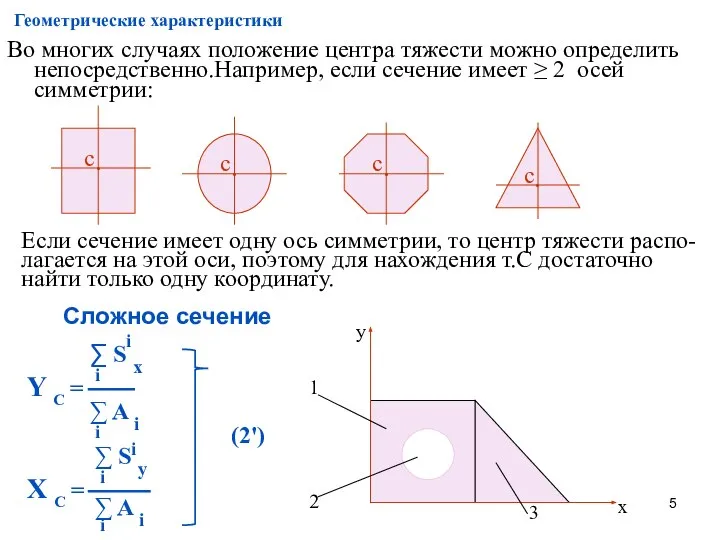
- 5. Геометрические характеристики Во многих случаях положение центра тяжести можно определить непосредственно.Например, если сечение имеет ≥ 2
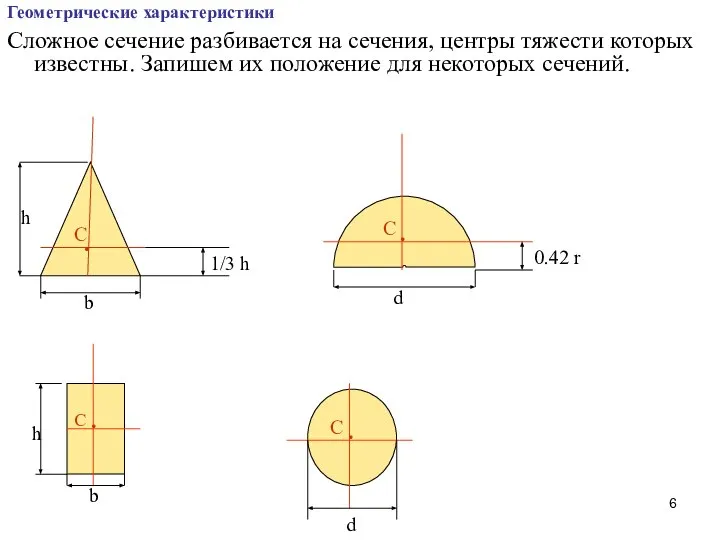
- 6. Геометрические характеристики Сложное сечение разбивается на сечения, центры тяжести которых известны. Запишем их положение для некоторых
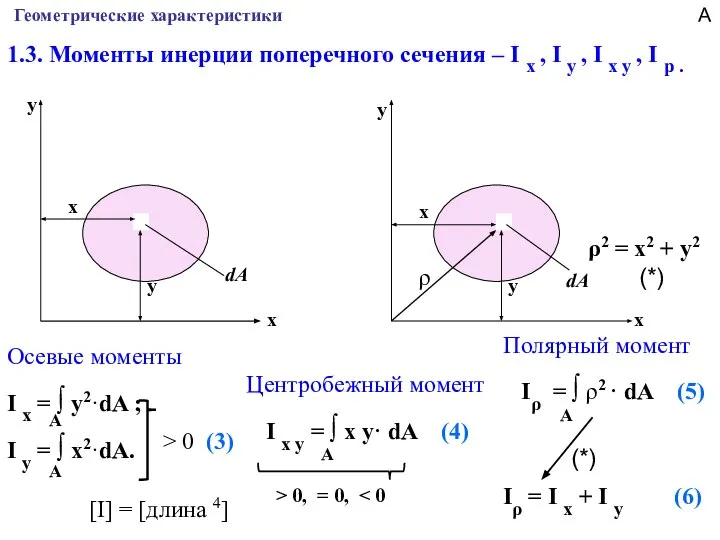
- 7. Геометрические характеристики 1.3. Моменты инерции поперечного сечения – I x , I y , I x
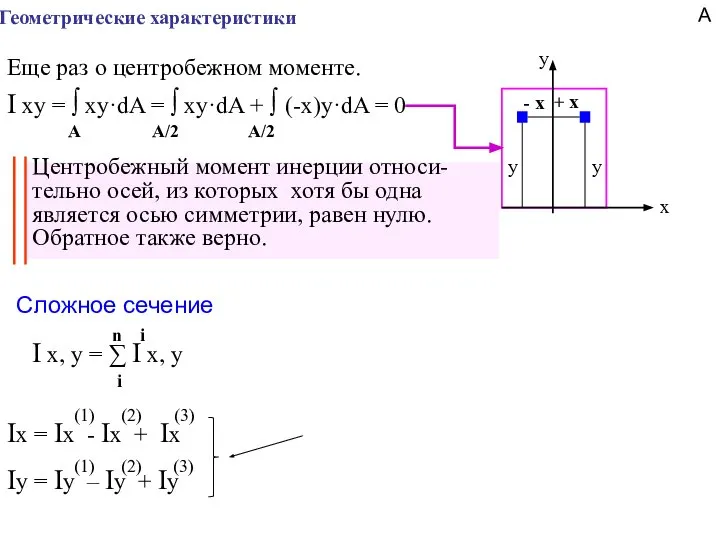
- 8. Геометрические характеристики Еще раз о центробежном моменте. y x y y + x - x I
- 9. Геометрические характеристики Центральные моменты инерции – моменты относительно центральных осей. Поскольку центральных осей – бесконечное множество,
- 10. Геометрические характеристики 1.4. Моменты инерции простейших сечений 1.5. Изменение моментов инерции при преобразовании осей Параллельный перенос
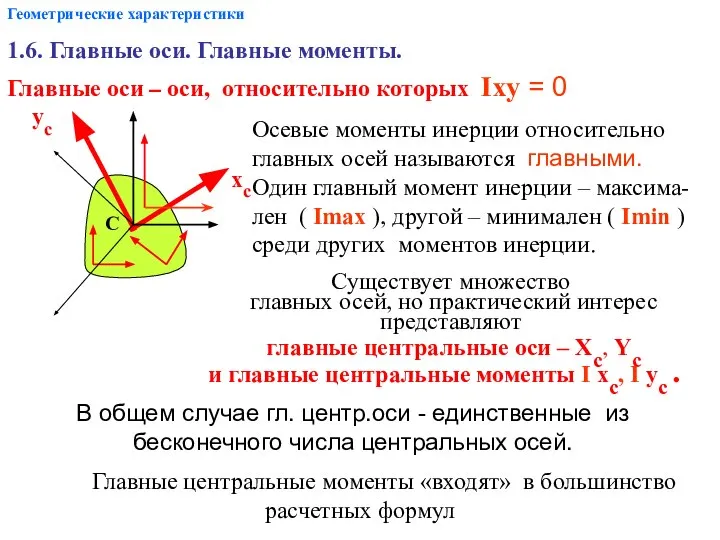
- 11. Геометрические характеристики 1.6. Главные оси. Главные моменты. Главные оси – оси, относительно которых Ixy = 0
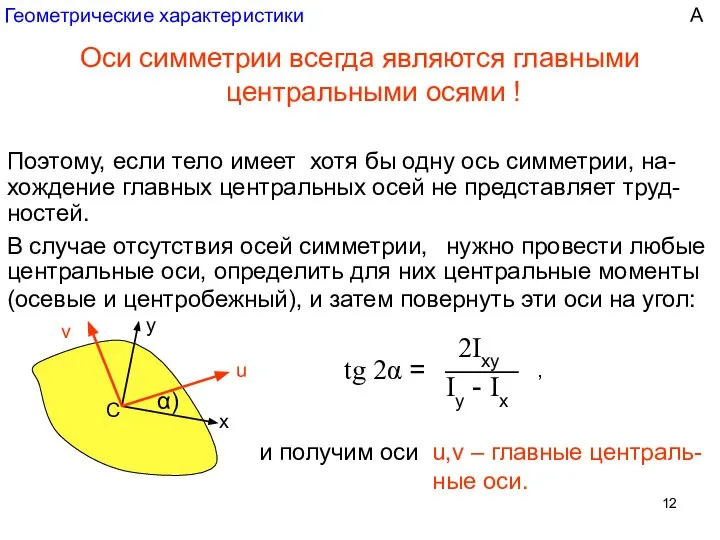
- 12. Геометрические характеристики Оси симметрии всегда являются главными центральными осями ! Поэтому, если тело имеет хотя бы
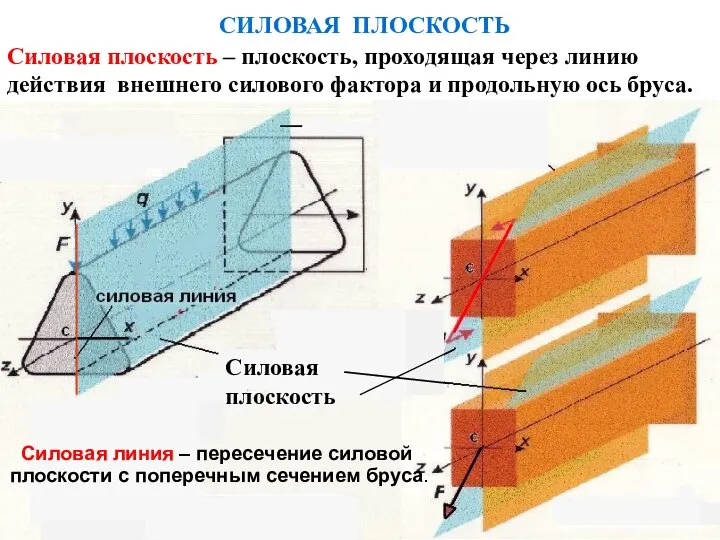
- 13. СИЛОВАЯ ПЛОСКОСТЬ Силовая плоскость Силовая плоскость – плоскость, проходящая через линию действия внешнего силового фактора и
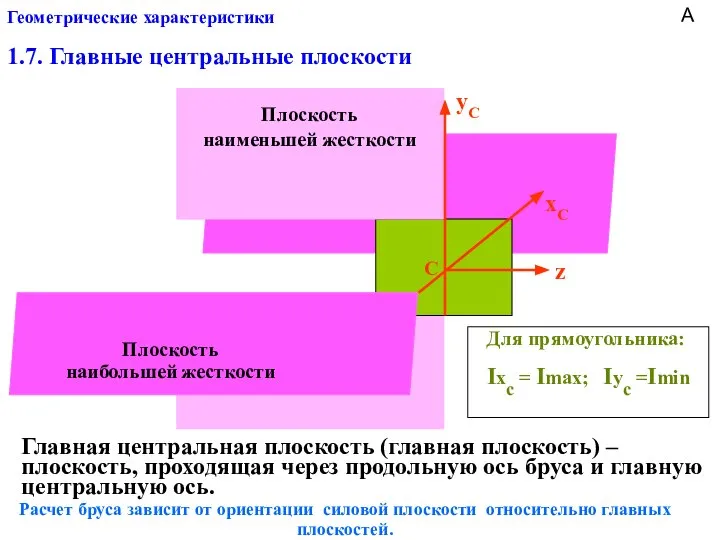
- 14. Геометрические характеристики 1.7. Главные центральные плоскости z xC yC Плоскость наименьшей жесткости Плоскость наибольшей жесткости С
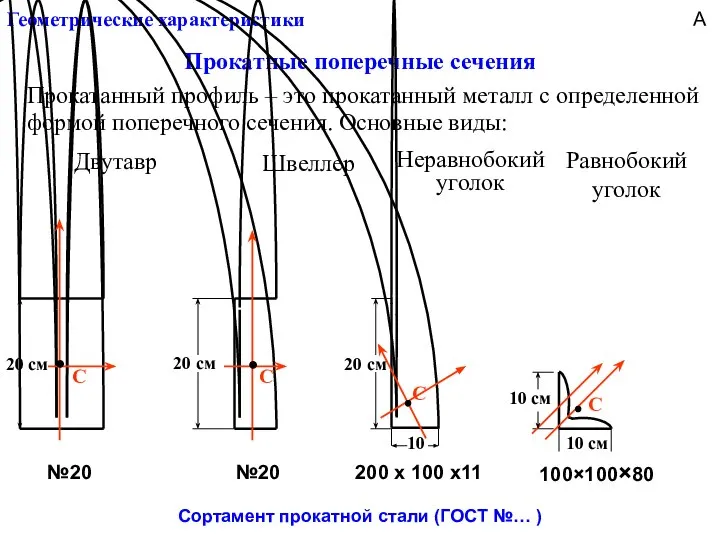
- 15. Геометрические характеристики Прокатные поперечные сечения Прокатанный профиль – это прокатанный металл с определенной формой поперечного сечения.
- 17. Скачать презентацию





 Открытия на большом адронном коллайдере
Открытия на большом адронном коллайдере Физика космоса, кружок. Космология в ОТО
Физика космоса, кружок. Космология в ОТО Дифракционная решётка
Дифракционная решётка Резка металла слесарной ножовкой
Резка металла слесарной ножовкой Тема 1.2 Нормир.точности. продолжение
Тема 1.2 Нормир.точности. продолжение Механические колебания
Механические колебания Солнце, воздух и вода – наши лучшие друзья
Солнце, воздух и вода – наши лучшие друзья Лекция 5_Физики_Основы термодинамики (1)
Лекция 5_Физики_Основы термодинамики (1) 671210
671210 Urok_Osnovy_MKT
Urok_Osnovy_MKT Многофакторное прогнозирование экологических характеристик дизеля на основе вычислительных методов
Многофакторное прогнозирование экологических характеристик дизеля на основе вычислительных методов Петля КМПЦ
Петля КМПЦ Работа, мощность. Энергия
Работа, мощность. Энергия Физические и химические явления. 8 класс
Физические и химические явления. 8 класс Подготовка к контрольной работе по физике
Подготовка к контрольной работе по физике Радиоактивность
Радиоактивность Презентация на тему Последовательное соединение проводников (8 класс)
Презентация на тему Последовательное соединение проводников (8 класс)  Презентация на тему Электробезопасность
Презентация на тему Электробезопасность  Театральные профессии: машинист сцены
Театральные профессии: машинист сцены Свободное падение тел
Свободное падение тел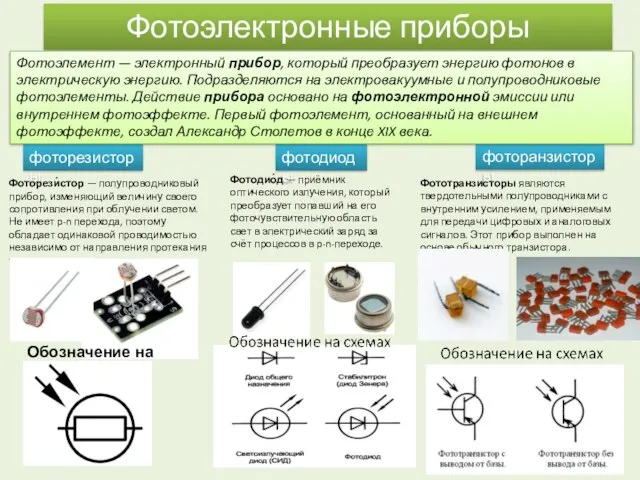 Фотоэлектронные приборы
Фотоэлектронные приборы Давление твердых тел
Давление твердых тел Измерение температуры с помощью термометра
Измерение температуры с помощью термометра Первый в мире паровой поезд когда и кем был изобретен
Первый в мире паровой поезд когда и кем был изобретен Энергия нужна всем!
Энергия нужна всем! Система питания инжекторного двигателя. Система распределенного впрыска LН-Getronic
Система питания инжекторного двигателя. Система распределенного впрыска LН-Getronic Количество теплоты
Количество теплоты Тепловые явления
Тепловые явления