Балочные системы. Определение реакций опор. (Тема 1.4.1)

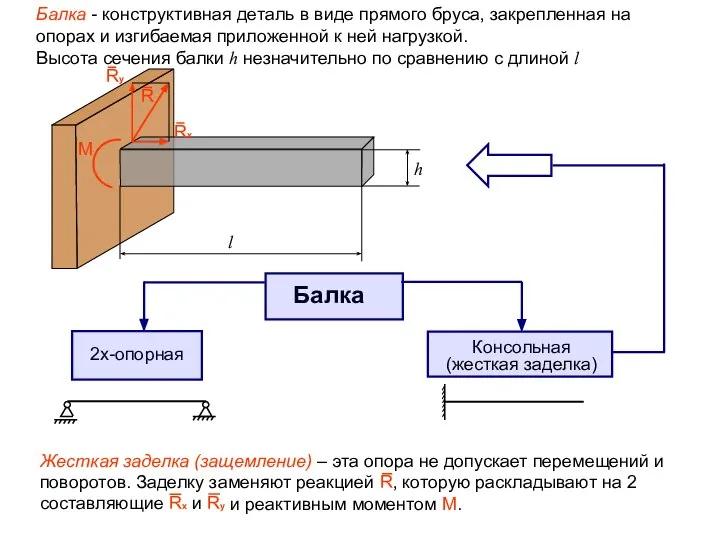
Балка - конструктивная деталь в виде прямого бруса, закрепленная на опорах и изгибаемая приложенной к ней нагрузкой.
l
h
Высота сечения балки h незначительно по сравнению с длиной l
Балка
2х-опорная
Консольная
(жесткая заделка)
Жесткая заделка (защемление) – эта опора не допускает перемещений и поворотов. Заделку заменяют реакцией R,
которую раскладывают на 2
составляющие Rx и Ry
и реактивным моментом М.
Ry
Rx
R
M

Для определения этих неизвестных удобно использовать систему уравнений в виде

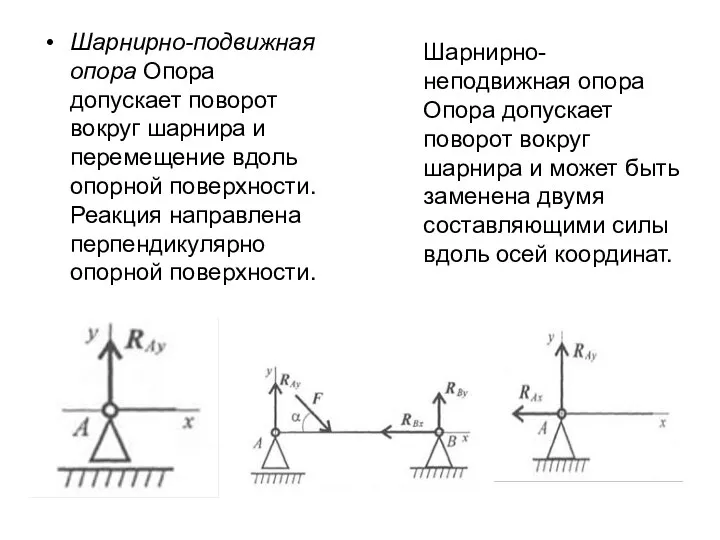
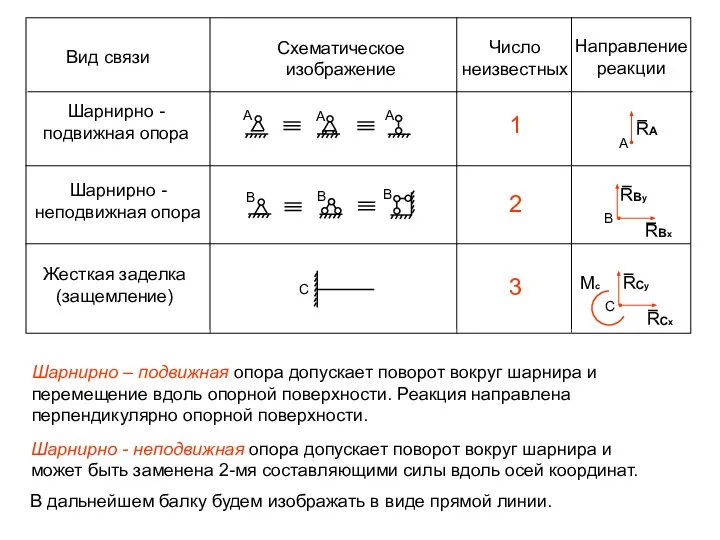
Шарнирно-подвижная опора Опора допускает поворот вокруг шарнира и перемещение вдоль опорной поверхности. Реак­ция направлена перпендикулярно опорной поверхности.
Шарнирно-неподвижная опора Опора допускает поворот вокруг шарнира и может быть заменена двумя составляющими силы вдоль осей координат.

Не известны три силы, две из них — вертикальные, следовательно, удобнее для определения неизвестных использовать систему уравнений во второй формуле:

Составляются уравнения моментов относительно точек крепления балки. Поскольку момент си-лы, проходящей через точку крепления, равен 0, в уравнении останется одна неизвестная сила.
Из уравнения определяется реакция Rbx.
Из уравнения определяется реакция Rby.
Из уравнения определяется реакция Ray.

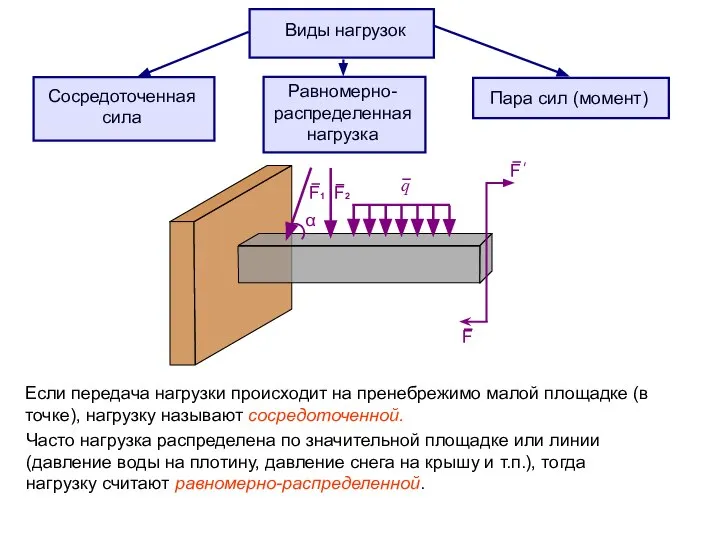
Виды нагрузок
Сосредоточенная сила
Равномерно-распределенная нагрузка
Пара сил (момент)
α
q
F
F
F1
F2
Если передача нагрузки происходит на пренебрежимо малой площадке (в точке), нагрузку называют сосредоточенной.
Часто нагрузка распределена по значительной площадке или линии (давление воды на плотину, давление снега на крышу и т.п.), тогда нагрузку считают равномерно-распределенной.

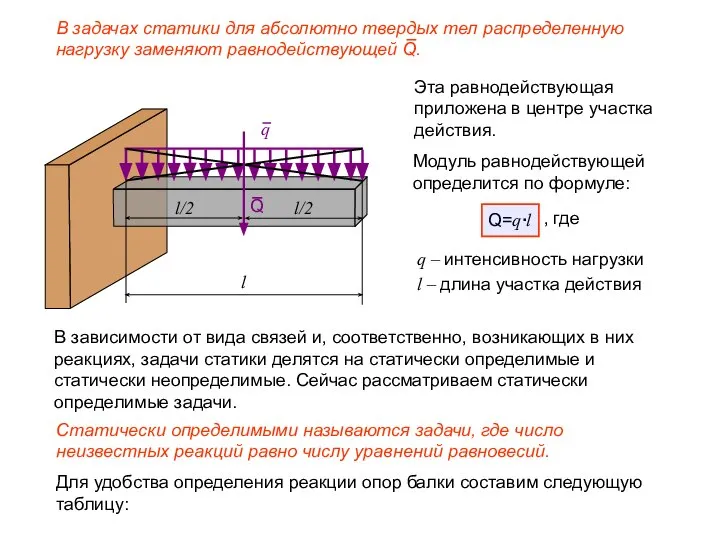
В задачах статики для абсолютно твердых тел распределенную нагрузку заменяют равнодействующей Q.
q
l
Q
l/2
l/2
Эта равнодействующая приложена в центре участка действия.
Модуль равнодействующей определится по формуле:
Q=q l
.
, где
q – интенсивность нагрузки
l – длина участка действия
В зависимости от вида связей и, соответственно, возникающих в них реакциях, задачи статики делятся на статически определимые и статически неопределимые. Сейчас рассматриваем статически определимые задачи.
Статически определимыми называются задачи, где число неизвестных реакций равно числу уравнений равновесий.
Для удобства определения реакции опор балки составим следующую таблицу:

Вид связи
Шарнирно - подвижная опора
Шарнирно - неподвижная опора
Жесткая заделка (защемление)
Схематическое изображение
Число неизвестных
Направление реакции
Шарнирно – подвижная опора допускает поворот вокруг шарнира и перемещение вдоль опорной поверхности. Реакция направлена перпендикулярно опорной поверхности.
Шарнирно - неподвижная опора допускает поворот вокруг шарнира и может быть заменена 2-мя составляющими силы вдоль осей координат.
А
А
А
В
В
В
С
1
2
3
А
В
С
RА
RВу
RВх
RСу
RСх
Мс
В дальнейшем балку будем изображать в виде прямой линии.

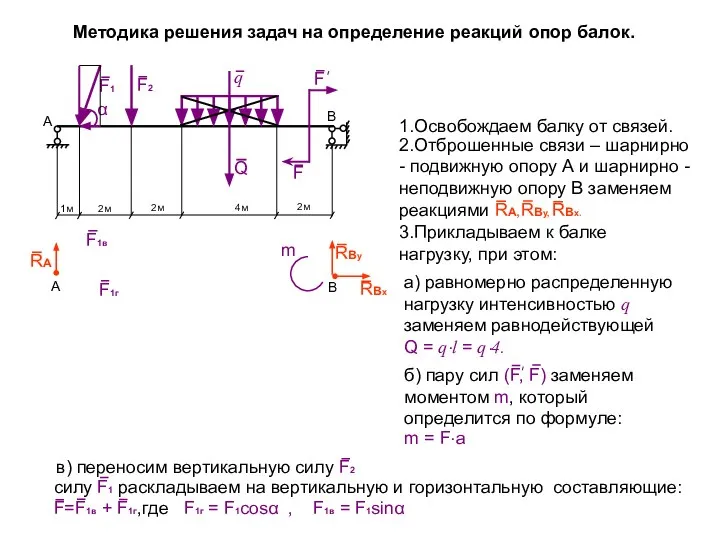
Методика решения задач на определение реакций опор балок.
А
В
1.Освобождаем балку от связей.
А
В
2.Отброшенные связи – шарнирно - подвижную опору А и шарнирно - неподвижную опору В заменяем реакциями
RА
RВу
RВх
α
q
F
F
F1
F2
1м
2м
2м
4м
2м
3.Прикладываем к балке нагрузку, при этом:
а) равномерно распределенную нагрузку интенсивностью q заменяем равнодействующей Q = q l = q 4.
.
Q
.
б) пару сил (F, F) заменяем моментом m, который определится по формуле:
m = F a
.
m
в) переносим вертикальную силу F2
силу F1 раскладываем на вертикальную и горизонтальную составляющие: F=F1в + F1г,
где F1г = F1cosα , F1в = F1sinα
RА,
RВу,
RВх.
F1г
F1в

А
В
RА
RВу
RВх
Q
m
F1г
F1в
F2
4) Определяем расстояние между линиями действия сил.
1м
2м
2м
4м
2м
1м
2м
4 м
4 м
5) К полученной системе сил применяем условия равновесия в форме (А),
∑Fkx=0
∑mА(Fk)=0
∑mВ(Fk)=0
предварительно выбрав оси координат.
у
х
; - F1г + RBx = 0 (1)
(2)
– m = 0
.
.
.
.
.
.
Составляем 3 ур – я равновесия:
Из каждого уравнения выражаем свои неизвестные:
из (1)
из (2) RBy =
m + Q 7 + F2 3 + F1B 1
.
.
.
11
из (3) RA =
11
F1B 10 + F2 8 + Q 4 – m
.
.
.
6) Осуществляем проверку правильности решения, составляя уравнение равновесия ∑Fkу=0 ; RA – F1B – F2 – Q + RB = 0
; RBy 11
- m
- Q 7
- F2 3
- F1B 1 = 0
.
11м
7м
3м
1м
; - RA 11
.
+ F1B 10
10м
+ F2 8
8 м
+ Q 4
4 м
(3)
RBx = F1г