Содержание
- 2. Цель работы — обобщение разработанной математической модели трехмерного квазистационарного электромагнитного поля вблизи поверхности объекта контроля, содержащего
- 3. Возникает необходимость управления топологией внешнего магнитного поля для получения более существенных искажений вихревых токов. Например, концентрация
- 4. Синхронная машина осевого потока Рис.1. 3D модель генератора осевого потока с постоянными магнитами.
- 6. Характеристики рассчитываемой машины
- 7. Трёхмерная модель магнитного поля магнит- ной системы машины осевого потока.
- 8. Численная модель простого слоя
- 9. Переопределение матрицы коэффициентов
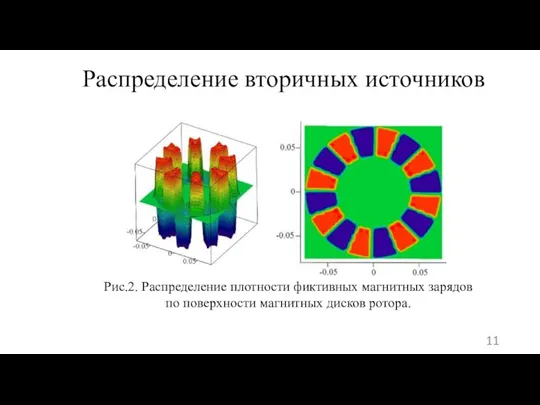
- 11. Распределение вторичных источников Рис.2. Распределение плотности фиктивных магнитных зарядов по поверхности магнитных дисков ротора.
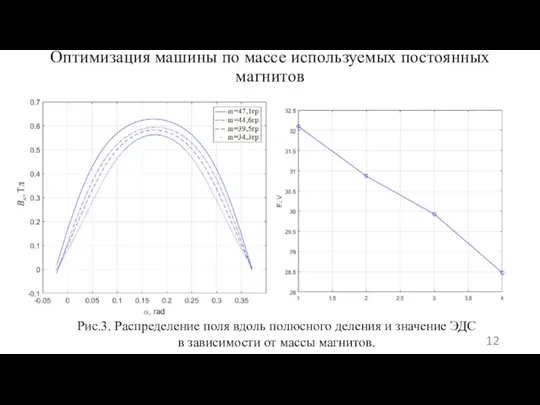
- 12. Оптимизация машины по массе используемых постоянных магнитов Рис.3. Распределение поля вдоль полюсного деления и значение ЭДС
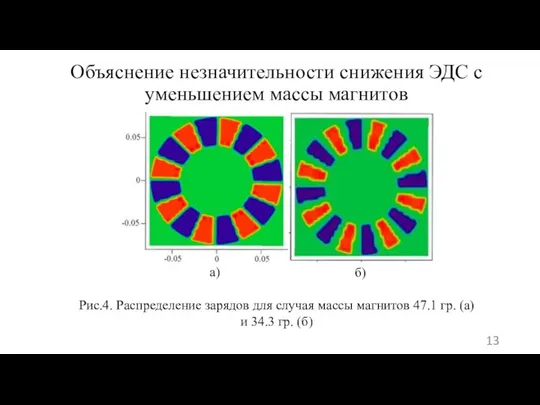
- 13. Объяснение незначительности снижения ЭДС с уменьшением массы магнитов Рис.4. Распределение зарядов для случая массы магнитов 47.1
- 14. Разработана математическая модель для расчёта поля ферромагнитного тела на основе метода двойного слоя магнитных зарядов. Данная
- 15. Численная модель метода двойного слоя, модифицированного в рамках подхода интегральных граничных соотношений
- 16. Рис.5. Иллюстрация выбора отрезков интегрирования. Особенности реализации: переопределение СЛАУ
- 17. Разработан алгоритм триангуляции с контролируемым шагом для случая поверхности произвольной трёхмерной многосвязной области. С использованием данного
- 18. Пример триангулированной геометрической области Рис.6. Триангуляция поверхности стального диска магнитопровода.
- 19. Выводы Разработана и реализована модель для расчёта магнитного поля ферромагнетика на основе метода простого слоя магнитных
- 21. Скачать презентацию















 Динамика вращательного движения
Динамика вращательного движения Подготовка к контрольной работе по физике
Подготовка к контрольной работе по физике Низкоэнергетическое лазерное излучение
Низкоэнергетическое лазерное излучение Методические указания к курсовому проекту по спецкурсу № 2. Теории ядерных реакторов
Методические указания к курсовому проекту по спецкурсу № 2. Теории ядерных реакторов Работа, мощность и энергия. Задачи
Работа, мощность и энергия. Задачи Элементарные частицы
Элементарные частицы Строение атома
Строение атома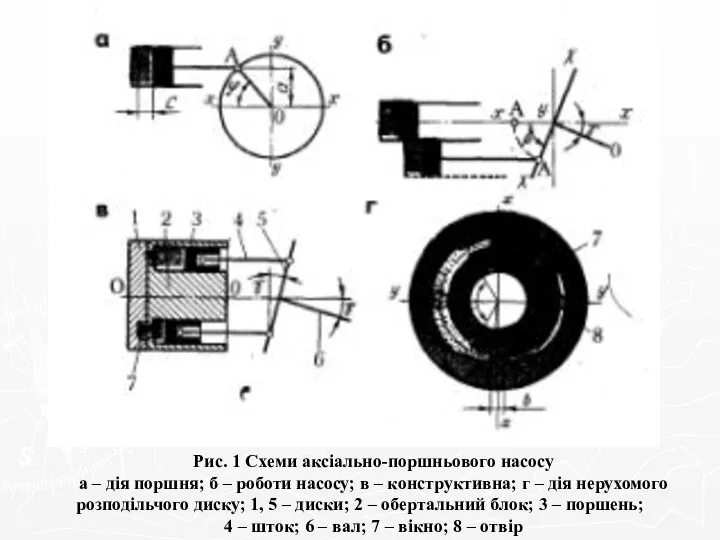 Схеми аксіально-поршньового насосу. Билет 8
Схеми аксіально-поршньового насосу. Билет 8 Электроемкость. Конденсаторы
Электроемкость. Конденсаторы Механика. Повторение. Занятие 7
Механика. Повторение. Занятие 7 Бензиновые двигатели
Бензиновые двигатели Механика и элементы специальной теории относительности. Лекция 1
Механика и элементы специальной теории относительности. Лекция 1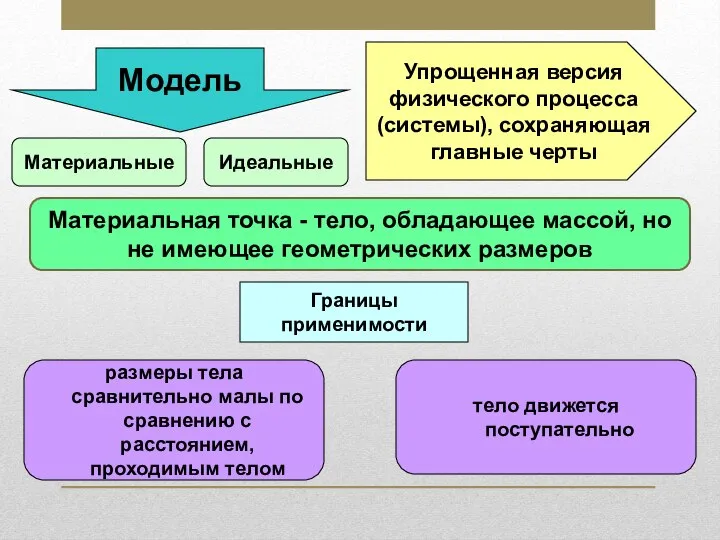 Материальная точка
Материальная точка Расчет сопротивления электрических цепей
Расчет сопротивления электрических цепей Автосцепное устройство
Автосцепное устройство Серво привод с электромеханическим распором
Серво привод с электромеханическим распором Физика в жизни
Физика в жизни Подшипники насосов и компрессоров
Подшипники насосов и компрессоров Тепловые двигатели
Тепловые двигатели Простые механизмы. Рычаг
Простые механизмы. Рычаг Реализация проекта строительства атомной электростанции в Республике Беларусь
Реализация проекта строительства атомной электростанции в Республике Беларусь Определение длины световой волны с помощью дифракционной решетки. Лабораторная работа № 3. 11класс
Определение длины световой волны с помощью дифракционной решетки. Лабораторная работа № 3. 11класс Энергия связи
Энергия связи Полупроводниковые материалы. Свойства полупроводниковых материалов. Лекция 1
Полупроводниковые материалы. Свойства полупроводниковых материалов. Лекция 1 Мир вокруг нас
Мир вокруг нас Заклёпочные соединения. Основные сведения и расчет на прочность
Заклёпочные соединения. Основные сведения и расчет на прочность Физические приборы вокруг нас
Физические приборы вокруг нас Презентация на тему Насыщенный пар
Презентация на тему Насыщенный пар