Содержание
- 2. Задачи, поставленные на второй семестр Суть нашего проекта заключается в моделировании и оптимизации траектории полетов космических
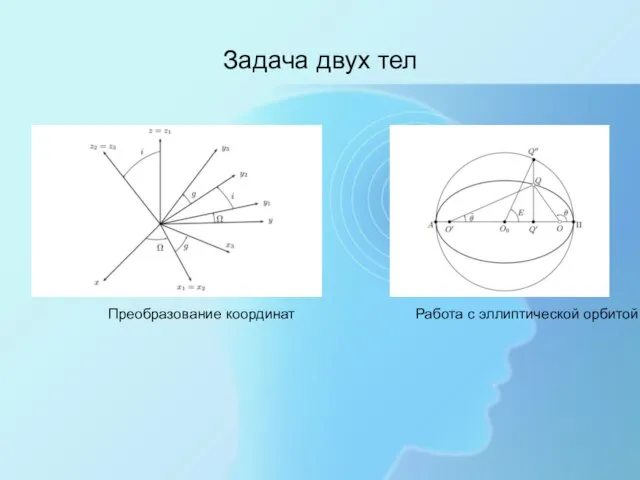
- 3. Задача двух тел
- 4. Задача двух тел Преобразование координат Работа с эллиптической орбитой
- 5. Задача Коши Рассмотрим одну из наиболее часто встречающихся задач — задачу Коши. По заданному условию находится
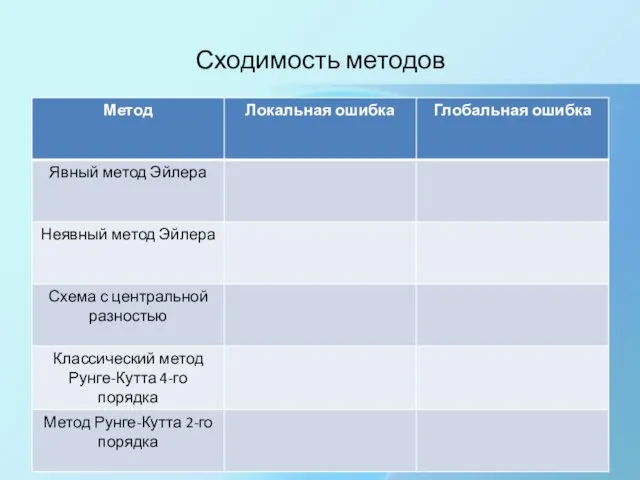
- 6. Сходимость методов
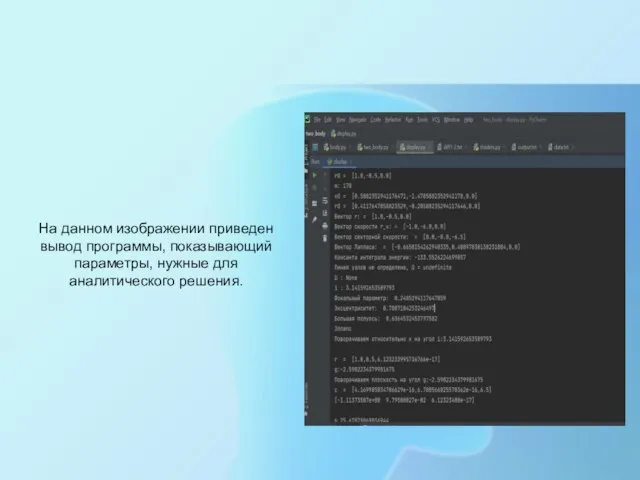
- 7. На данном изображении приведен вывод программы, показывающий параметры, нужные для аналитического решения.
- 8. Пример работы программы
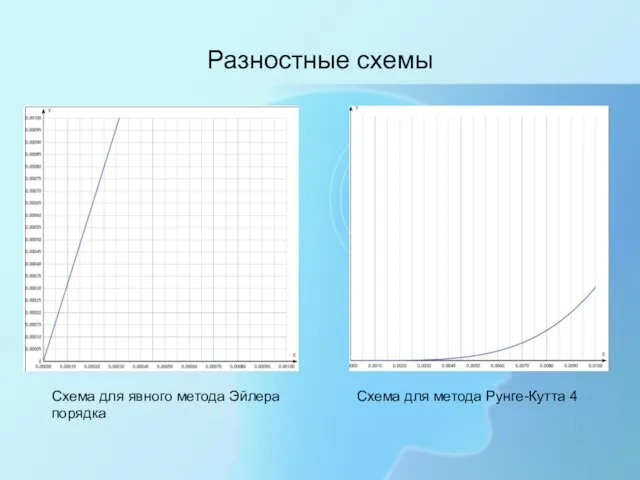
- 10. Разностные схемы Схема для явного метода Эйлера Схема для метода Рунге-Кутта 4 порядка
- 11. Список литературы: [1] Федоренко Р.П., «Введение в вычислительную физику». – 1994 [2] Калиткин Н.Н., «Численные методы».
- 13. Процесс решения задачи Построение математической модели заданного физического процесса Компьютерное моделирование процесса при помощи построенной математической
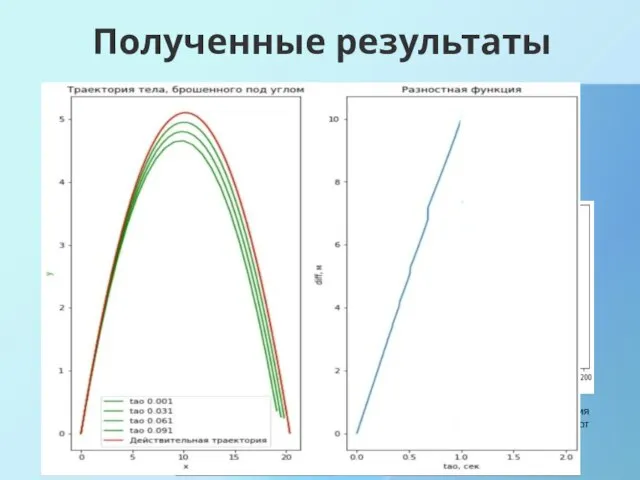
- 14. Полученные результаты При решении задачи о движении тел, брошенного под углом к горизонту, использовались такие физические
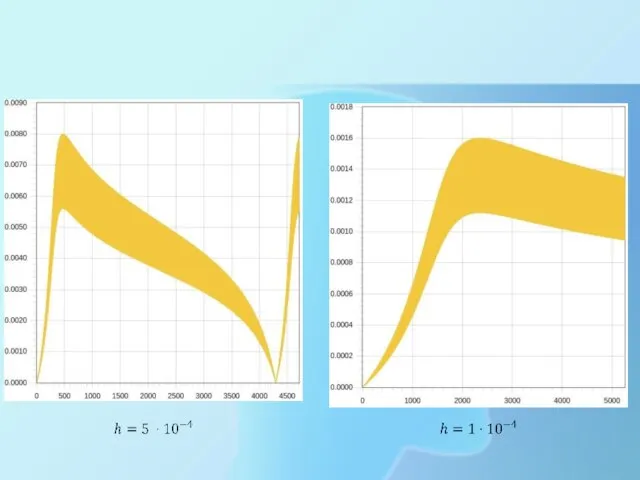
- 15. Полученные результаты Полученная численными методами траектория Зависимость максимального отклонения численного и аналитических решений от величины разбиения
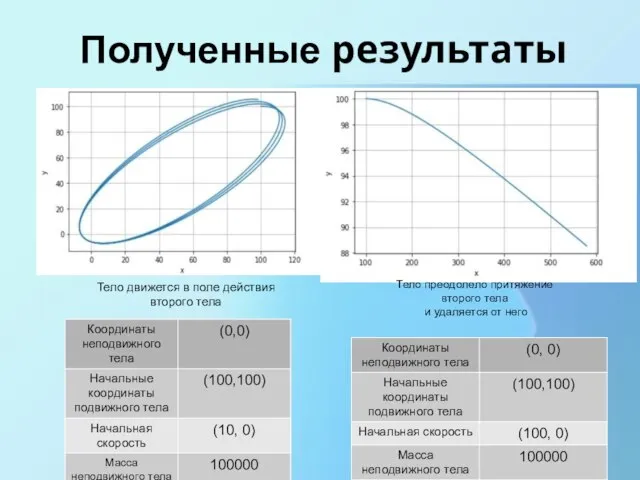
- 16. Полученные результаты Далее была решена задача, в которой рассматривается два тела, одно из которых покоится, А
- 17. Полученные результаты Тело движется в поле действия второго тела Тело преодолело притяжение второго тела и удаляется
- 18. В данный момент мы решаем, так называемую, задачу двух тел. Её формулировка следующая: даны два тела,
- 19. Задача двух тел
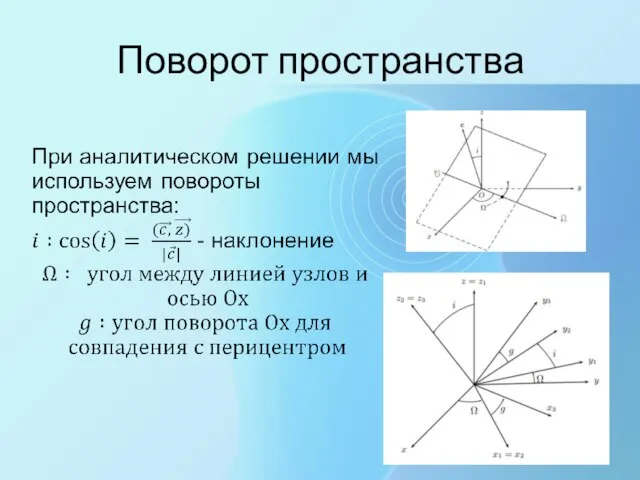
- 20. Поворот пространства
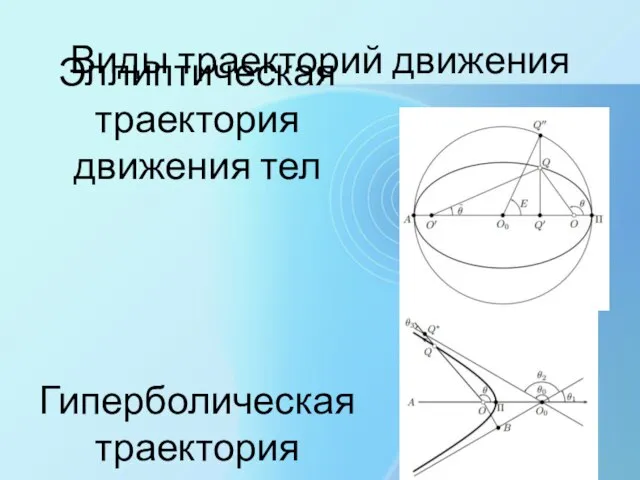
- 21. Виды траекторий движения Эллиптическая траектория движения тел Гиперболическая траектория движения тел
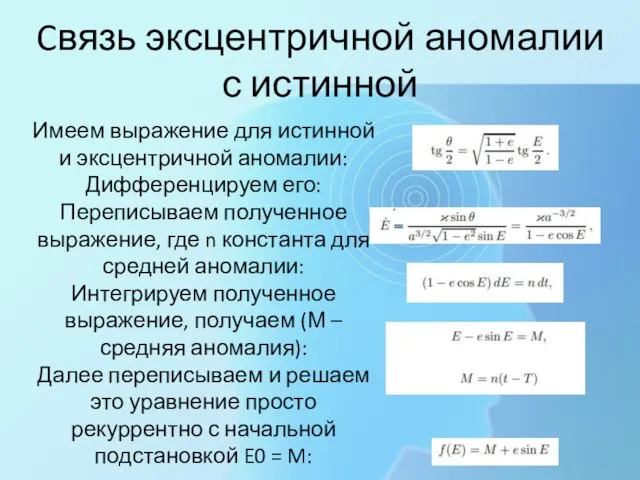
- 22. Имеем выражение для истинной и эксцентричной аномалии: Дифференцируем его: Переписываем полученное выражение, где n константа для
- 23. По своей сути, задача двух тел – один из случаев задачи Коши, рассмотренной ранее. Метод Рунге-Кутты
- 24. Явные методы Рунге-Кутта
- 25. Метод Рунге - Кутты с автоматическим выбором шага
- 27. Оптимизация траектории - процесс проектирования траектории, который сводит к минимуму (или максимизирует) некоторую меру производительности при
- 28. Прямой метод решения задачи оптимизации траектории состоит из двух этапов: 1) Непосредственно дискретизировать задачу оптимизации траектории,
- 29. Одиночная стрельба – ограничение дефекта на всем сегменте Многократная стрельба – ограничение дефекта на множестве сегментов
- 31. Скачать презентацию




![Список литературы: [1] Федоренко Р.П., «Введение в вычислительную физику». – 1994 [2]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/858640/slide-10.jpg)












 ИГЭС 2 семестр-Волны Лекция 2
ИГЭС 2 семестр-Волны Лекция 2 Презентация на тему Решение задач импульс, работа. энергия
Презентация на тему Решение задач импульс, работа. энергия  Виды зубчатых передач
Виды зубчатых передач Преломление света. Дисперсия. Цвета тел. (6 класс)
Преломление света. Дисперсия. Цвета тел. (6 класс) Презентация на тему Строение атома Квантовая физика
Презентация на тему Строение атома Квантовая физика  Состав ядра атома. Энергия связи атомных ядер. Дефект масс
Состав ядра атома. Энергия связи атомных ядер. Дефект масс Электрический ток в различных средах
Электрический ток в различных средах Методы регистрации заряженных частиц
Методы регистрации заряженных частиц Физика твердой Земли. Стационарное тепловое поле
Физика твердой Земли. Стационарное тепловое поле Постоянный ток и его основные законы
Постоянный ток и его основные законы Назначение, классификация и конструкция колесных пар локомотива
Назначение, классификация и конструкция колесных пар локомотива Сложение сил
Сложение сил Волновая оптика
Волновая оптика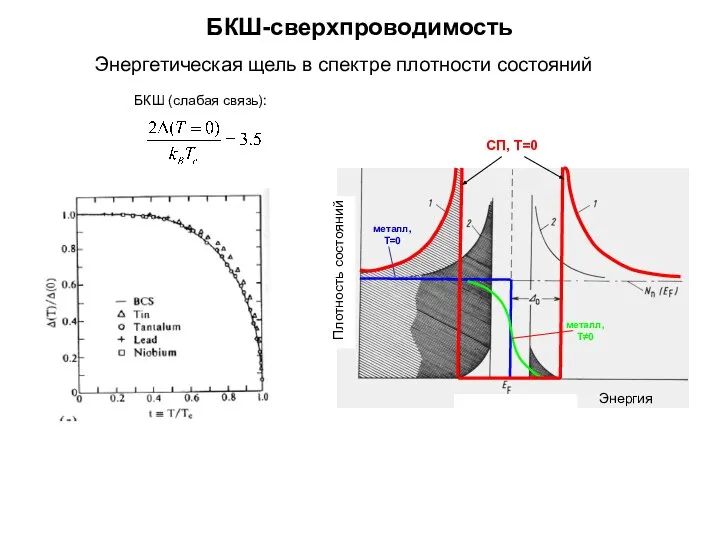 БКШ-сверхпроводимость. Терагерцовая оптика
БКШ-сверхпроводимость. Терагерцовая оптика Презентация на тему Скорость света
Презентация на тему Скорость света  Презентация на тему Закон Ома
Презентация на тему Закон Ома  Основы расчетов на жесткость деталей машин. Лекция 7
Основы расчетов на жесткость деталей машин. Лекция 7 tormoznaya_sistema_TO
tormoznaya_sistema_TO 540576.pptx
540576.pptx Основы термодинамики
Основы термодинамики Фотоядерные реакции. (Тема 2.5)
Фотоядерные реакции. (Тема 2.5) Поляризация диэлектриков
Поляризация диэлектриков Ножницы как рычаг
Ножницы как рычаг Ламповый генератор
Ламповый генератор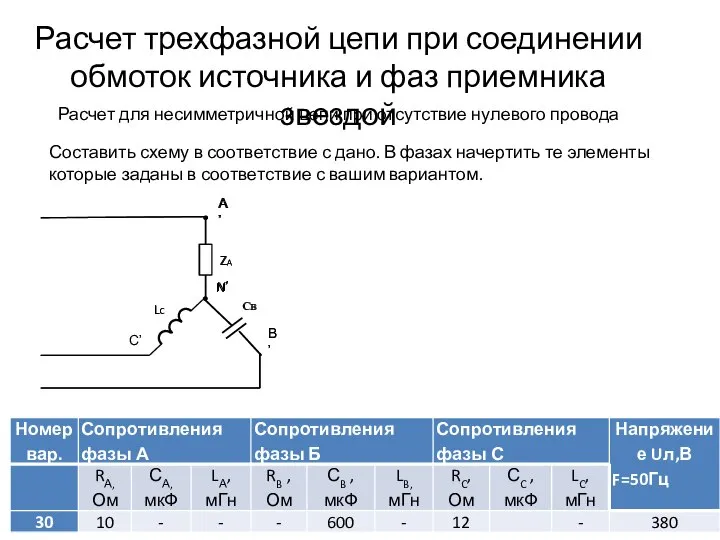 Расчет трехфазной цепи при соединении обмоток источника и фаз приемника звездой
Расчет трехфазной цепи при соединении обмоток источника и фаз приемника звездой Период полураспада. Закон радиоактивного распада
Период полураспада. Закон радиоактивного распада Квазихимический метод описания дефектов
Квазихимический метод описания дефектов Цепи переменного тока с последовательным соединением элементов
Цепи переменного тока с последовательным соединением элементов