Содержание
- 2. Основные предпосылки и гипотезы Рассматриваются линейно деформируемые системы. 2. Исходное состояние – равновесие при статических (квазистатических)
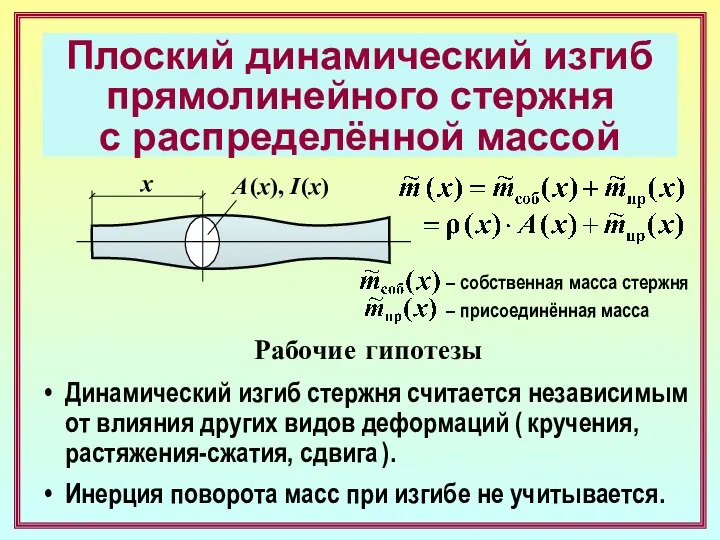
- 3. Плоский динамический изгиб прямолинейного стержня с распределённой массой Рабочие гипотезы Динамический изгиб стержня считается независимым от
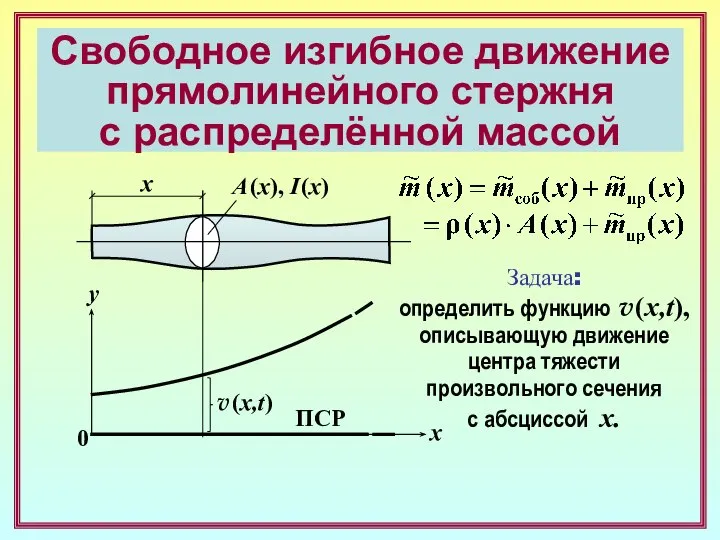
- 4. Свободное изгибное движение прямолинейного стержня с распределённой массой x A (x), I (x) x y 0
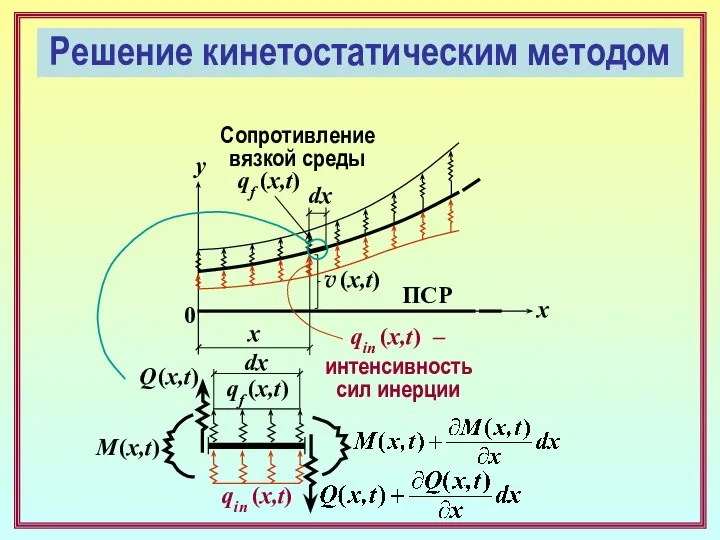
- 5. x x y 0 ПСР v (x,t) qf (x,t) Сопротивление вязкой среды qin (x,t) – интенсивность
- 6. Уравнения состояния элемента dx 1. Уравнения равновесия (статика) Q (x,t) M (x,t) qf (x,t) qin (x,t)
- 7. Уравнения состояния элемента dx 1. Уравнения равновесия (статика) Q (x,t) M (x,t) qf (x,t) qin (x,t)
- 8. Дифференциальное уравнение свободного изгибного движения прямолинейного стержня переменной жёсткости с неравномерно распределённой массой (сопротивление вязкой среды
- 9. Частные случаи дифференциального уравнения свободного изгибного движения прямолинейного стержня 2. Стержень постоянной жёсткости EI с равномерно
- 10. Общее решение уравнения (А) по методу Фурье: Частный случай – собственные изгибные колебания: Дифференциальное уравнение амплитуд
- 11. Характеристическое уравнение дифференциального уравнения (В): r4 – k4 = 0 r1 = k , r2 =
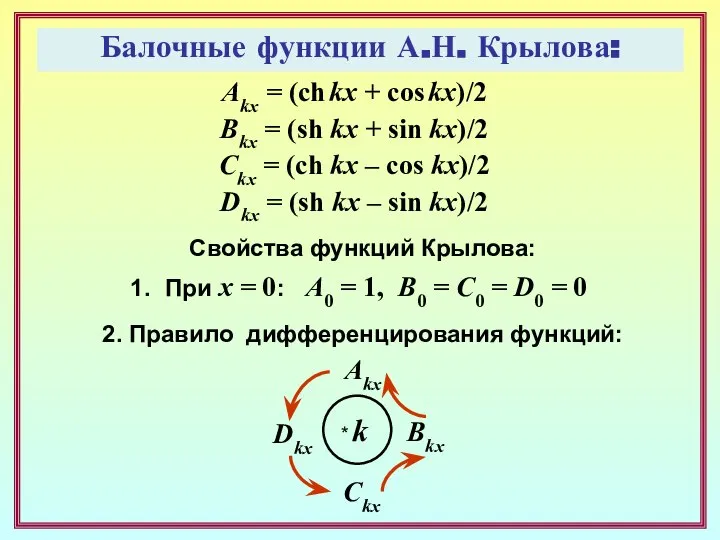
- 12. Балочные функции А.Н. Крылова: Akx = (ch kx + cos kx)/2 Bkx = (sh kx +
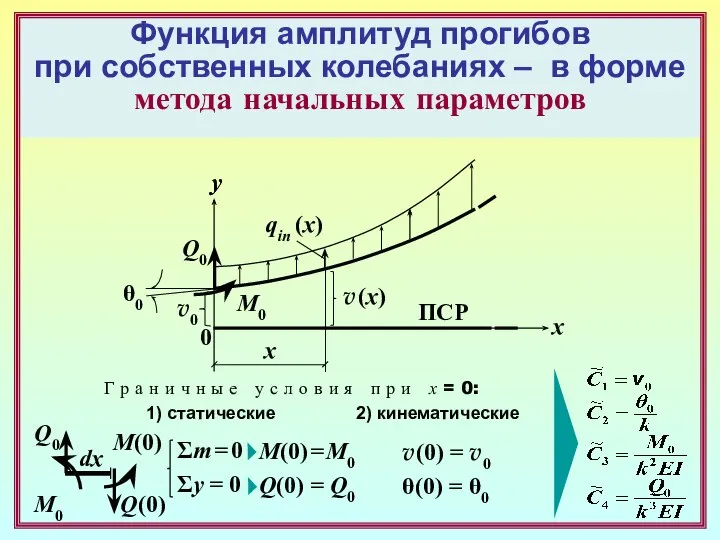
- 13. Функция амплитуд прогибов при собственных колебаниях – в форме метода начальных параметров x x y 0
- 14. Функция амплитуд прогибов при собственных колебаниях – в форме метода начальных параметров x x y 0
- 15. Функции амплитуд характеристик НДС при собственных колебаниях – в форме метода начальных параметров
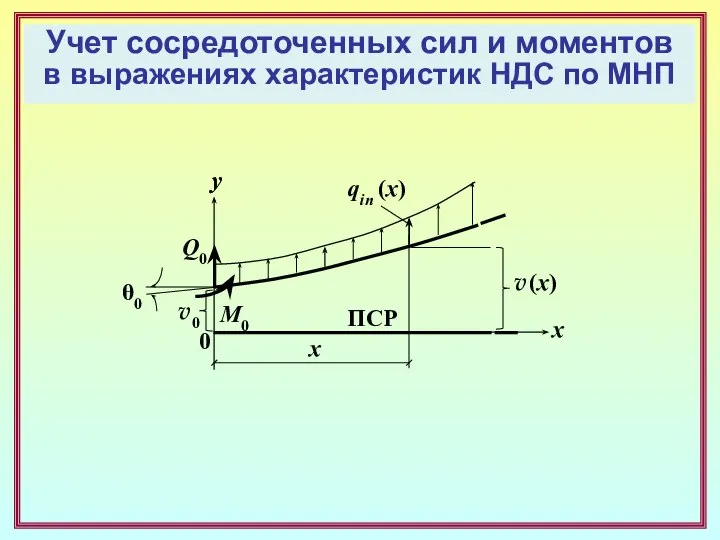
- 16. Учет сосредоточенных сил и моментов в выражениях характеристик НДС по МНП x y 0 ПСР v
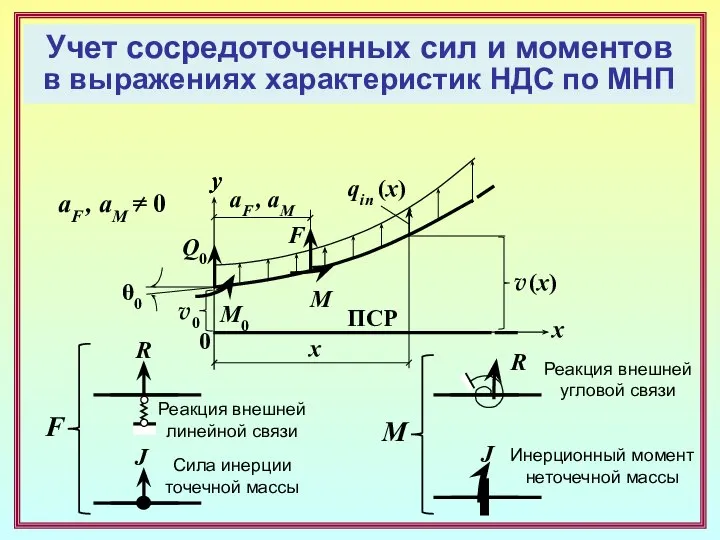
- 17. x F y 0 ПСР v (x) y qin (x) v0 θ0 Q0 M0 aF ,
- 18. x F y 0 ПСР v (x) y qin (x) v0 θ0 Q0 M0 aF ,
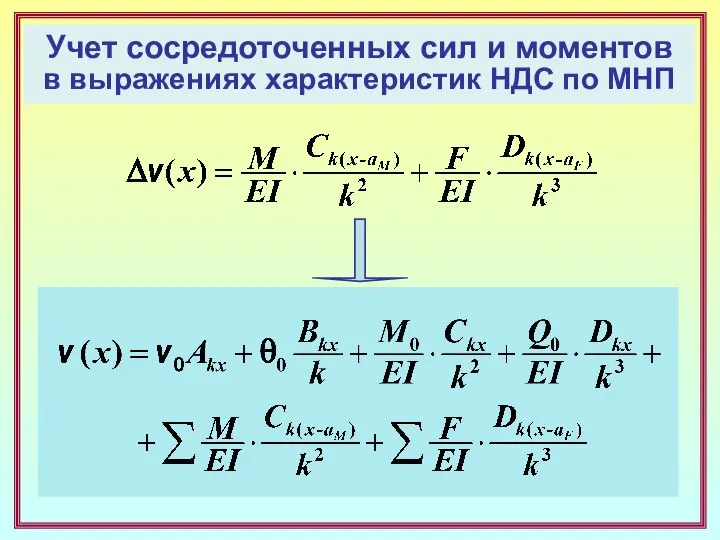
- 19. Учет сосредоточенных сил и моментов в выражениях характеристик НДС по МНП
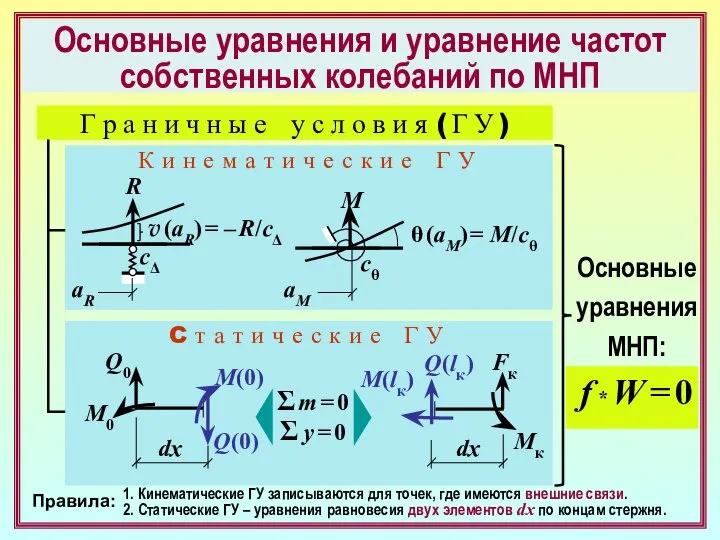
- 20. Основные уравнения и уравнение частот собственных колебаний по МНП Г р а н и ч н
- 21. Основные уравнения и уравнение частот собственных колебаний по МНП f * W = 0 v0 θ0
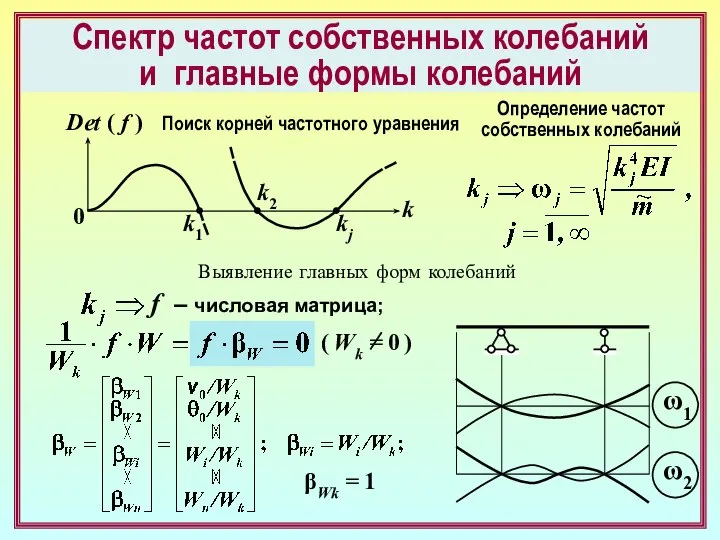
- 22. Спектр частот собственных колебаний и главные формы колебаний Det ( f ) k 0 k1 k2
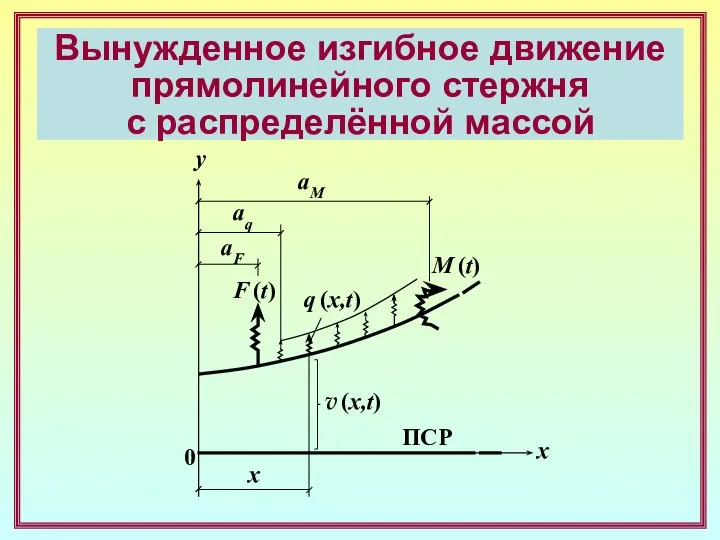
- 23. Вынужденное изгибное движение прямолинейного стержня с распределённой массой x x y 0 ПСР v (x,t) q
- 24. x x y 0 ПСР v (x,t) q (x,t) F (t) aM aq aF Решение кинетостатическим
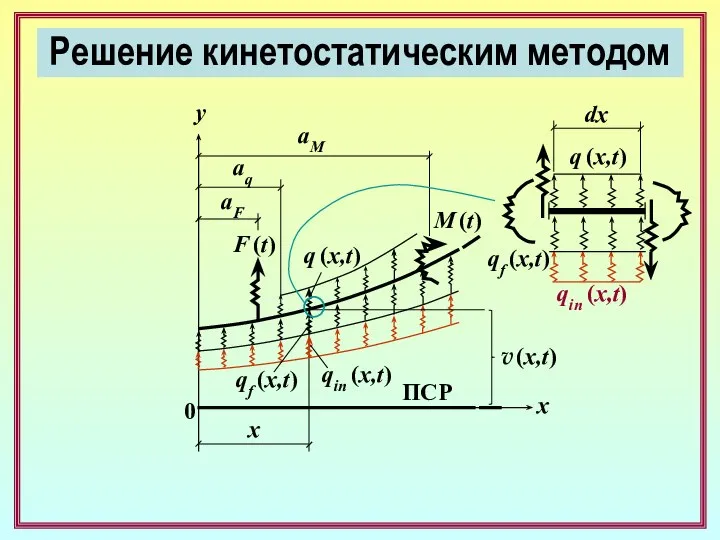
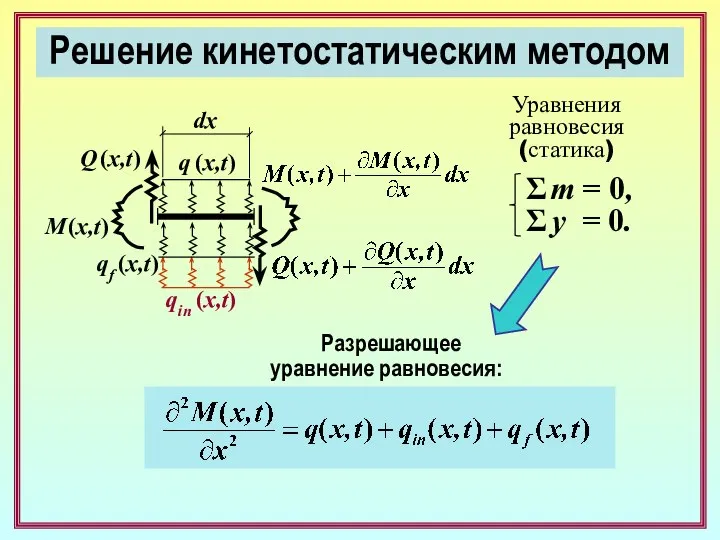
- 25. Решение кинетостатическим методом M (x,t) Уравнения равновесия (статика) q (x,t) qin (x,t) qf (x,t) dx Q
- 26. Дифференциальное уравнение вынужденного изгибного движения прямолинейного стержня переменной жёсткости с неравномерно распределённой массой (сопротивление вязкой среды
- 27. Частный случай – дифференциальное уравнение вынужденного изгибного движения прямолинейного стержня переменной жёсткости с неравномерно распределённой массой
- 28. Решение дифференциального уравнения v(x,t) = v(x,t)+ v*(x,t) v(x,t) – общее решение однородного диф. уравнения v*(x,t) –
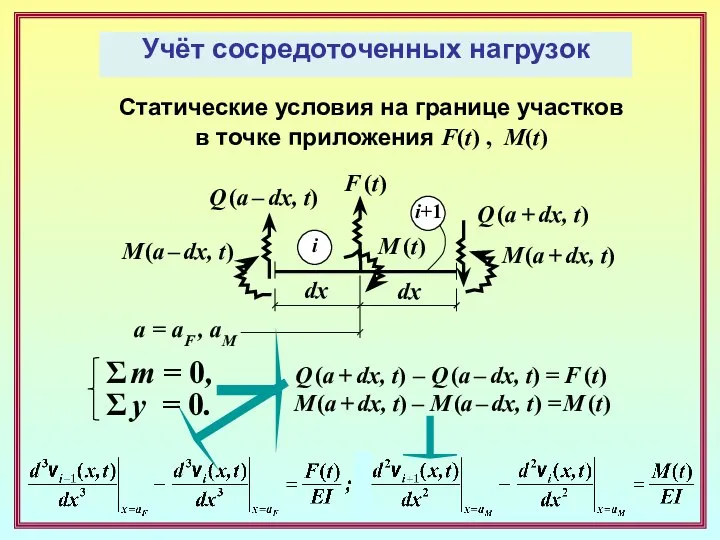
- 29. Учёт сосредоточенных нагрузок Статические условия на границе участков в точке приложения F(t) , M(t) F (t)
- 30. Установившиеся вынужденные изгибные колебания прямолинейного стержня постоянной жёсткости с равномерно распределённой массой, без учёта демпфирования (
- 31. Установившиеся вынужденные изгибные колебания прямолинейного стержня постоянной жёсткости с равномерно распределённой массой, без учёта демпфирования (
- 32. К о н т р о л ь н ы е в о п р о
- 34. Скачать презентацию

















 Переменный электрический ток
Переменный электрический ток Механические колебания. Колебательные движения
Механические колебания. Колебательные движения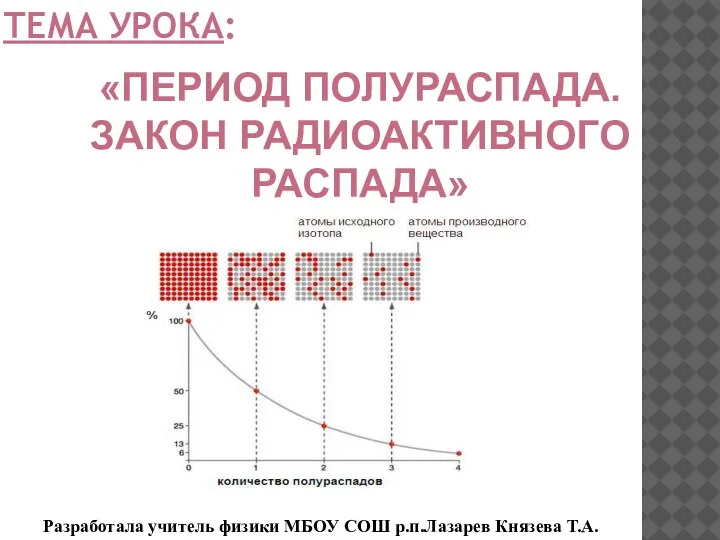 Закон радиоактивного распада. Период полураспада радиоактивных изотопов
Закон радиоактивного распада. Период полураспада радиоактивных изотопов Prüfen und Einstellen
Prüfen und Einstellen Статистическая теория радиотехнических систем. Задача фильтрации. (Лекция 13)
Статистическая теория радиотехнических систем. Задача фильтрации. (Лекция 13) Потенциал электростатического поля
Потенциал электростатического поля Переменный электрический ток. 11 класс
Переменный электрический ток. 11 класс Электромагнитные явления
Электромагнитные явления Движение твердой среды. Теорема Эйлера
Движение твердой среды. Теорема Эйлера Теория происходящего: инерция
Теория происходящего: инерция Потенциально-обратные двухполюсники и условия их взаимной обратимости
Потенциально-обратные двухполюсники и условия их взаимной обратимости Основы проектирования
Основы проектирования Автомобили III
Автомобили III Три состояния вещества
Три состояния вещества Решение задач на расчет пути и времени равномерного движения
Решение задач на расчет пути и времени равномерного движения Лист лотоса. Оптические и СЗМ изображения
Лист лотоса. Оптические и СЗМ изображения Колебательное движение
Колебательное движение Электромагнитная индукция
Электромагнитная индукция Работа измерительного прибора ИРК-ПРО
Работа измерительного прибора ИРК-ПРО Строение атома
Строение атома Презентация на тему Техника безопасности на уроках физики
Презентация на тему Техника безопасности на уроках физики  Решение задач по теме Соединение проводников
Решение задач по теме Соединение проводников Использование здоровьеформирующей технологии Ю.Г.Иванова на уроках физики
Использование здоровьеформирующей технологии Ю.Г.Иванова на уроках физики Сопротивляемость человеческого тела в разных условиях
Сопротивляемость человеческого тела в разных условиях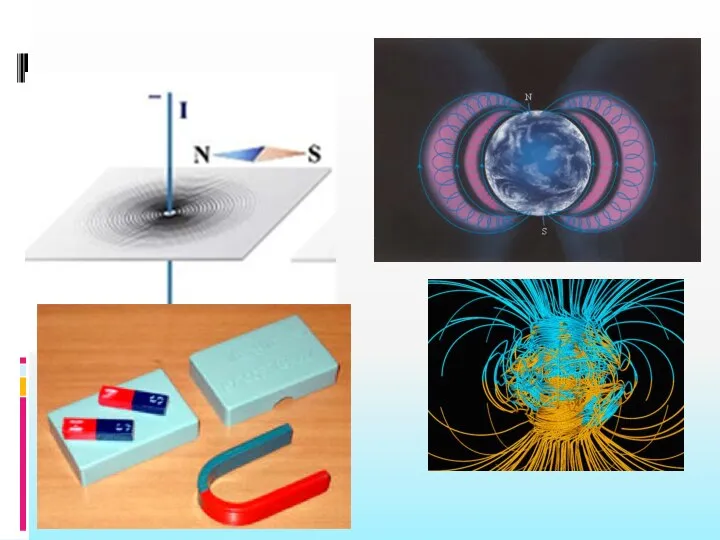 Магнитное поле. Решение задач
Магнитное поле. Решение задач Как сохранить энергию?
Как сохранить энергию? Лабораторная работа Определение положения центра тяжести плоской фигуры
Лабораторная работа Определение положения центра тяжести плоской фигуры Иондық каландар мен тасымалдаушылар кұрылысы мен қызметі. Электрогенез механизмі
Иондық каландар мен тасымалдаушылар кұрылысы мен қызметі. Электрогенез механизмі