Сила Лоренца. Закон Ампера. Теорема Гаусса для вектора магнитной индукции. Лекция 20

Сила Лоренца
Рассмотрим движущийся заряд, на который действует магнитное поле.
Сила, действующая на электрический заряд q, движущийся в магнитном поле со скоростью , называется силой Лоренца:
Лоренц
Хендрик Антон
1853 - 1928

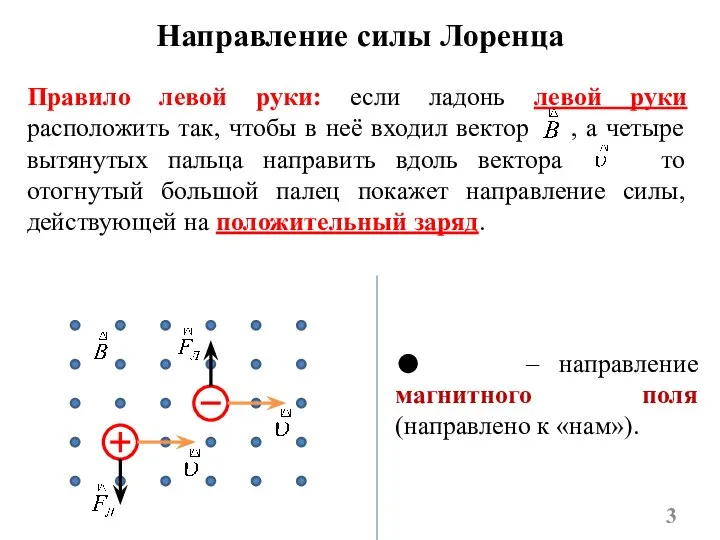
Направление силы Лоренца
Правило левой руки: если ладонь левой руки расположить так, чтобы в неё входил вектор , а четыре вытянутых пальца направить вдоль вектора то отогнутый большой палец покажет направление силы, действующей на положительный заряд.
– направление магнитного поля (направлено к «нам»).

1) Сила Лоренца всегда перпендикулярна скорости движения заряженной частицы;
2) Сила Лоренца изменяет только направление этой скорости, не изменяя её модуля.
Следовательно, сила Лоренца работы не совершает.
3) Кинетическая энергия этой частицы при движении в магнитном поле не изменяется.

Свойства силы Лоренца
Сила Лоренца действует только на движущиеся заряды
(υ ≠ 0); – сила Лоренца отсутствует;
2) Величина силы Лоренца зависит от угла α между направлением движения и вектором
– сила Лоренца максимальна.

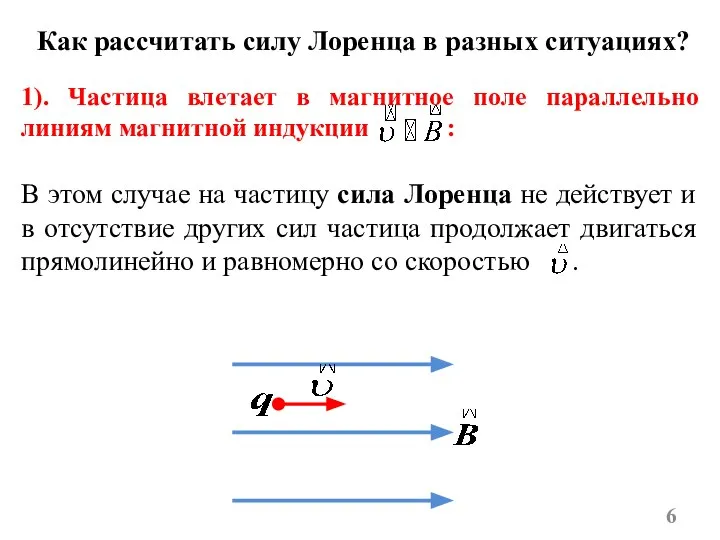
Как рассчитать силу Лоренца в разных ситуациях?
1). Частица влетает в магнитное поле параллельно линиям магнитной индукции :
В этом случае на частицу сила Лоренца не действует и в отсутствие других сил частица продолжает двигаться прямолинейно и равномерно со скоростью .

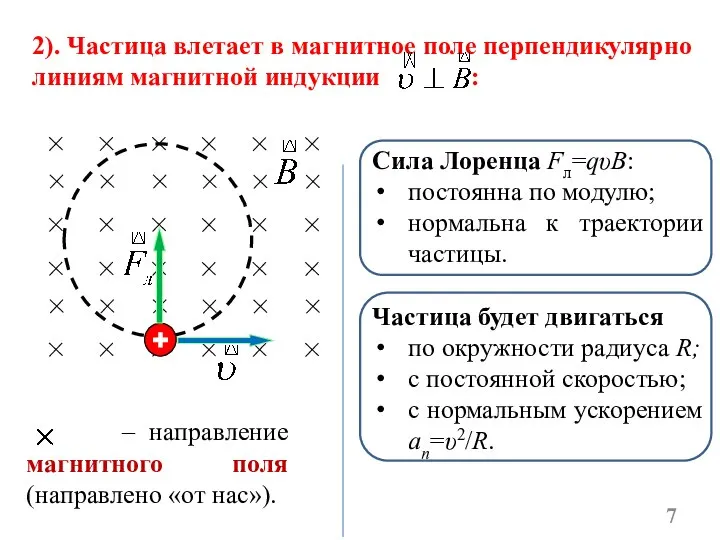
2). Частица влетает в магнитное поле перпендикулярно линиям магнитной индукции :
Сила Лоренца Fл=qυB:
постоянна по модулю;
нормальна к траектории частицы.
Частица будет двигаться
по окружности радиуса R;
с постоянной скоростью;
с нормальным ускорением an=υ2/R.

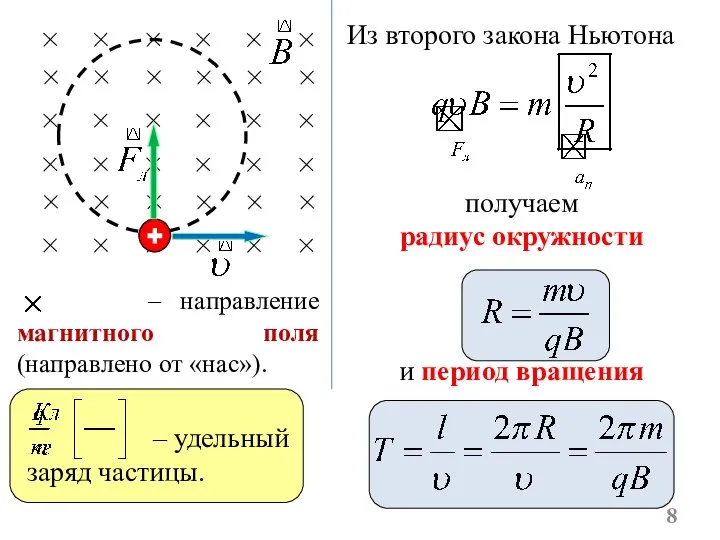
– направление магнитного поля (направлено от «нас»).
Из второго закона Ньютона
получаем
радиус окружности
и период вращения
– удельный заряд частицы.

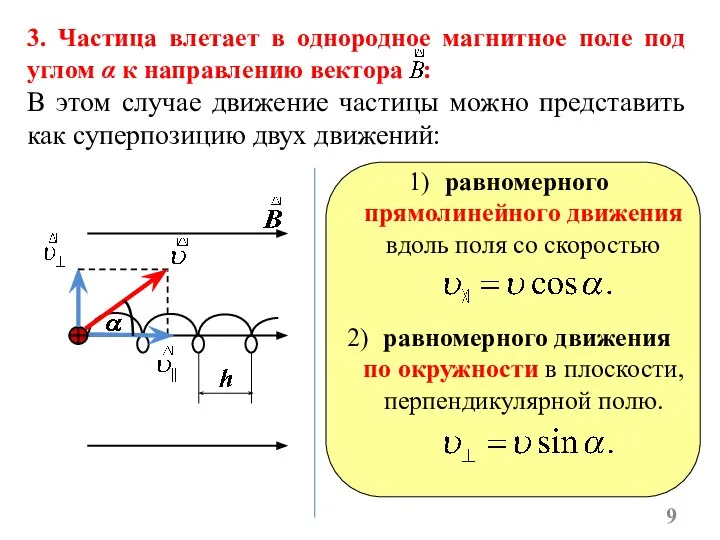
3. Частица влетает в однородное магнитное поле под углом α к направлению вектора :
В этом случае движение частицы можно представить как суперпозицию двух движений:
равномерного прямолинейного движения вдоль поля со скоростью
равномерного движения по окружности в плоскости, перпендикулярной полю.

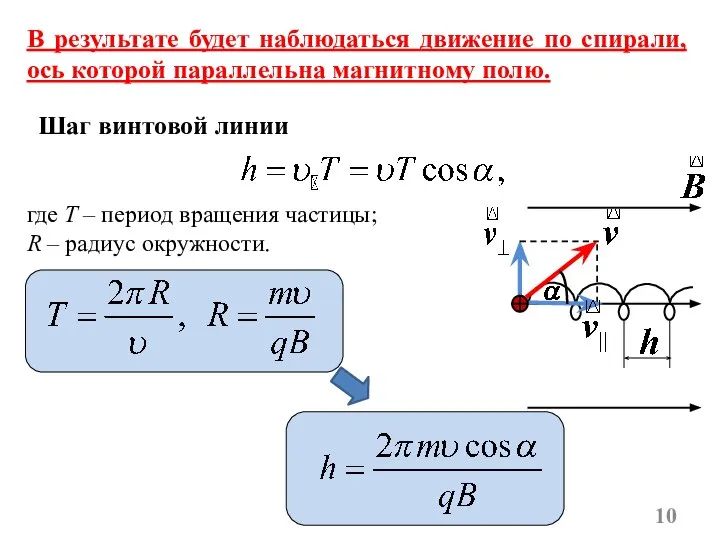
В результате будет наблюдаться движение по спирали, ось которой параллельна магнитному полю.
где T – период вращения частицы;
R – радиус окружности.
Шаг винтовой линии

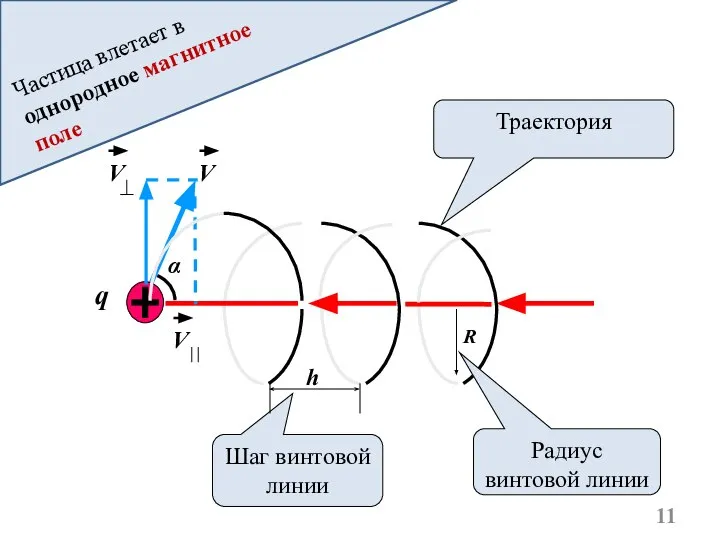
Шаг винтовой линии
Радиус винтовой линии
R
h
α
Частица влетает в однородное магнитное поле

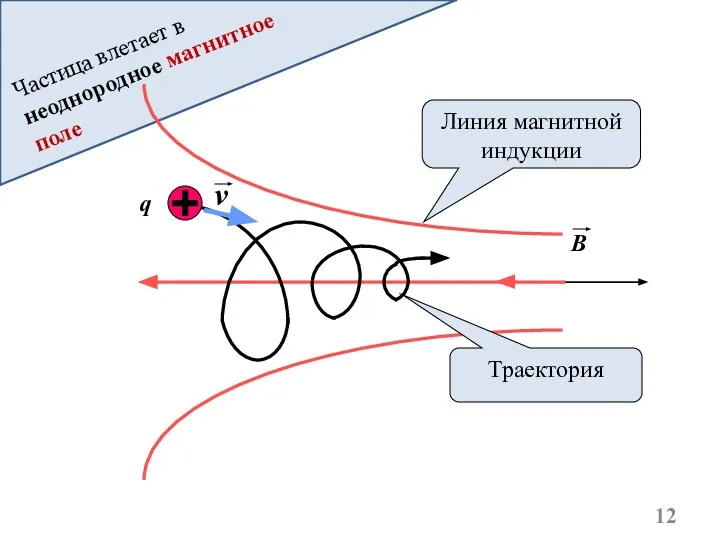
Частица влетает в неоднородное магнитное поле
Линия магнитной индукции
Траектория
q
B

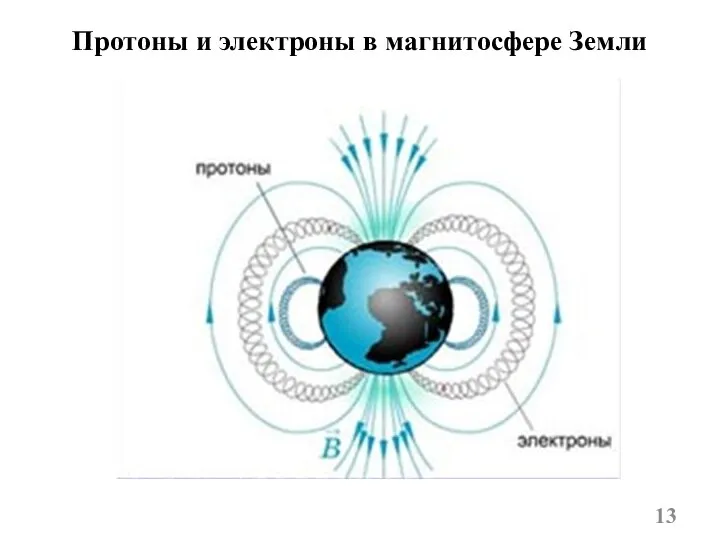
Протоны и электроны в магнитосфере Земли

Магнитное поле свободно движущегося заряда
Любой движущийся заряд является частным случаем электрического тока в проводнике.
Магнитное поле точечного заряда , свободно движущегося с постоянной нерелятивистской скоростью
где – радиус-вектор, проведенный из заряда q к точке наблюдения; α – угол между и .

Закон Ампера.
Механизм возникновения силы Ампера
Если провод, по которому течёт ток, находится в магнитном поле, на каждый движущийся носитель тока (электрон) в проводнике действует сила Лоренца
Под действием этой силы электрон, за время между столкновениями с ионами кристаллической решетки, получает дополнительный импульс
Ампер
Андре – Мари
1775 - 1836
В среднем, на каждый движущийся носитель тока (электрон) в проводнике действует сила Лоренца

Сталкиваясь с ионом решетки, электрон передаёт ему этот импульс (з-н сохранения импульса):
Если импульс иона изменяется, значит, на него действует сила:
Сила Ампера, действующая на проводник с током в магнитном поле, равняется равнодействующей сил Лоренца, действующих на все носители тока в этом проводнике.

Найдём силу , действующую на элемент проводника dl.
n – концентрация носителей тока в проводнике (1/м3);
– общее число носителей тока в элементе проводника dl.
Равнодействующая действующих на носители тока сил Лоренца равна:
Мы уже знаем, что

Таким образом
Заменив
получим,
Закон Ампера: сила , с которой магнитное поле действует на элемент проводника с током I, находящегося в магнитном поле, равна
– вектор, по модулю равный и совпадающий по направлению с током ;
– вектор магнитной индукции.
(направления j и l совпадают)

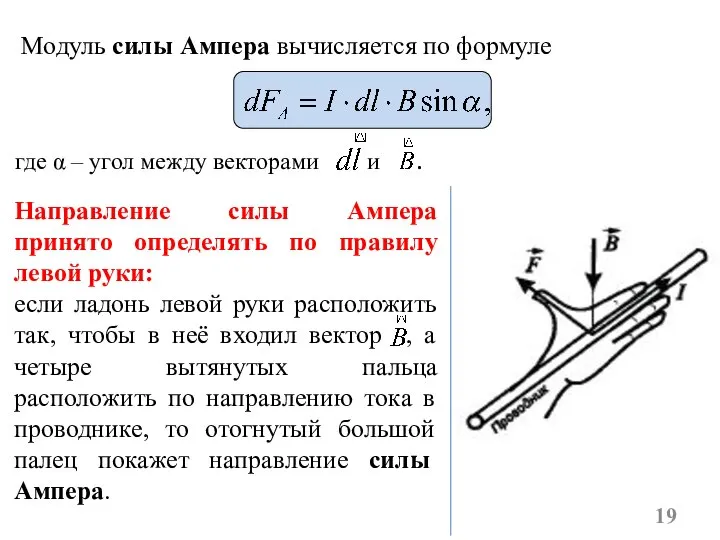
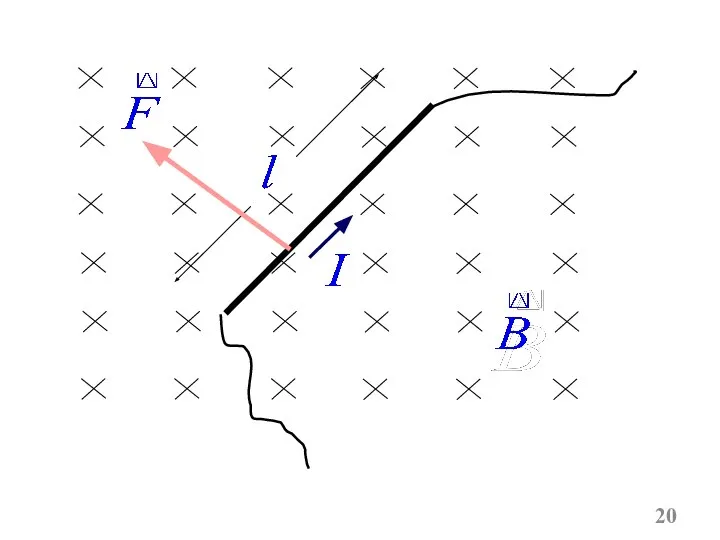
Модуль силы Ампера вычисляется по формуле
где α – угол между векторами и .
Направление силы Ампера принято определять по правилу левой руки:
если ладонь левой руки расположить так, чтобы в неё входил вектор , а четыре вытянутых пальца расположить по направлению тока в проводнике, то отогнутый большой палец покажет направление силы Ампера.

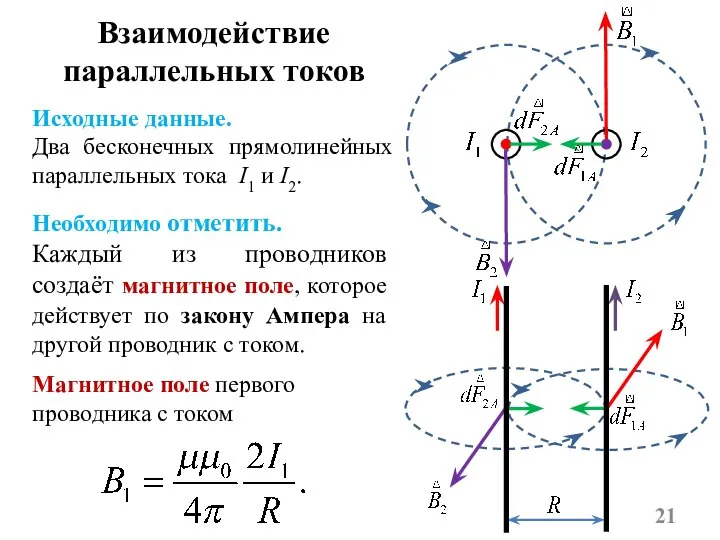
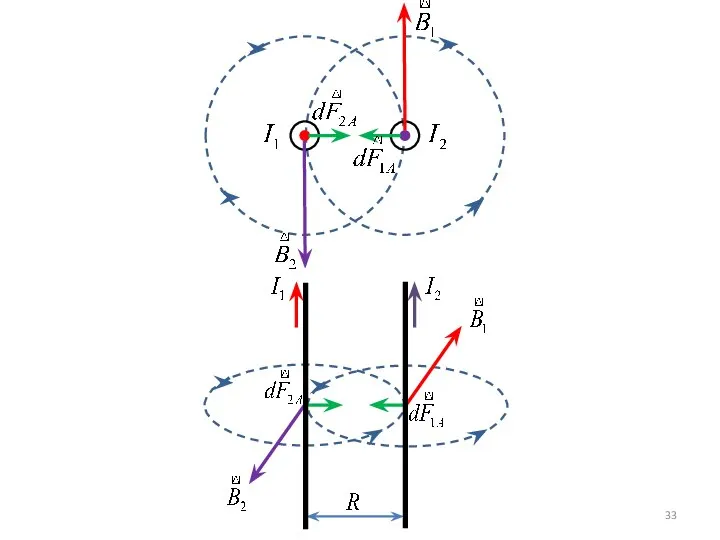
Взаимодействие параллельных токов
Магнитное поле первого проводника с током
Исходные данные.
Два бесконечных прямолинейных параллельных тока I1 и I2.
Необходимо отметить.
Каждый из проводников создаёт магнитное поле, которое действует по закону Ампера на другой проводник с током.

Аналогично сила dF2 равна
Модуль силы dF1 с учётом того, что угол α между элементами тока I2 и вектором прямой, равен
Подставив значение для B1, получим
Вывод:
Проводники с токами одинакового направления притягиваются,
с токами разного направления – отталкиваются.

Единицы магнитной индукции
Пусть элемент проводника dl с током I перпендикулярен направлению магнитного поля. По закону Ампера dF=Ibdl, откуда
Единица магнитной индукции B – тесла (Тл) – магнитная индукция такого однородного магнитного поля, которое действует с силой 1 Н на каждый метр длины прямолинейного проводника, расположенного перпендикулярно направлению поля, если по этому проводнику проходит ток 1 А:

Взаимосвязь магнитного поля и движущихся зарядов

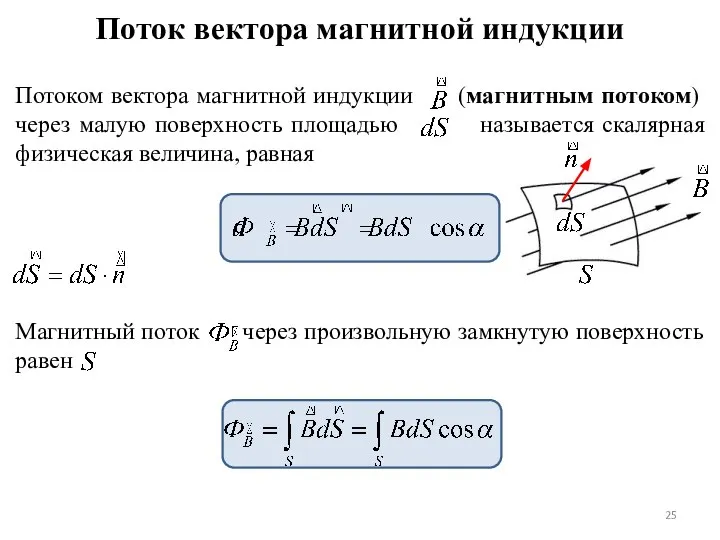
Поток вектора магнитной индукции
Потоком вектора магнитной индукции (магнитным потоком) через малую поверхность площадью называется скалярная физическая величина, равная
Магнитный поток через произвольную замкнутую поверхность равен

Отсутствие в природе магнитных зарядов приводит к тому, что линии вектора не имеют ни начала, ни конца.
Поэтому поток вектора через замкнутую поверхность должен быть равен нулю.
Теорема Гаусса для вектора магнитной индукции
Линии магнитной индукции замкнуты, поэтому число линий, входящих в некоторый объем пространства, равно числу линий, выходящих из этого объема.
Если входящие потоки брать с одним знаком, а выходящие — с другим, то суммарный поток вектора магнитной индукции через замкнутую поверхность будет равен нулю.

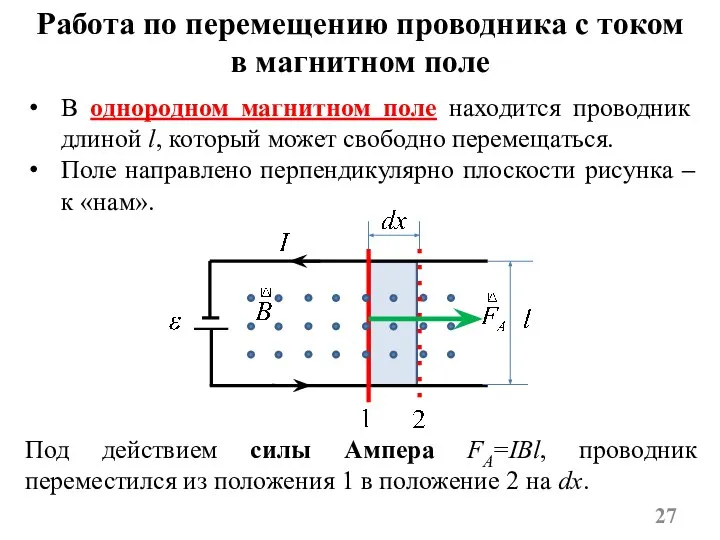
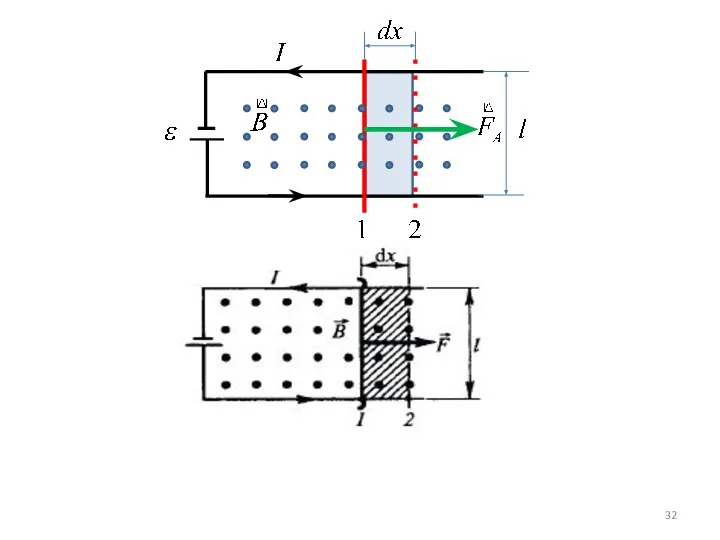
Работа по перемещению проводника с током
в магнитном поле
Под действием силы Ампера FА=IBl, проводник переместился из положения 1 в положение 2 на dx.
В однородном магнитном поле находится проводник длиной l, который может свободно перемещаться.
Поле направлено перпендикулярно плоскости рисунка – к «нам».

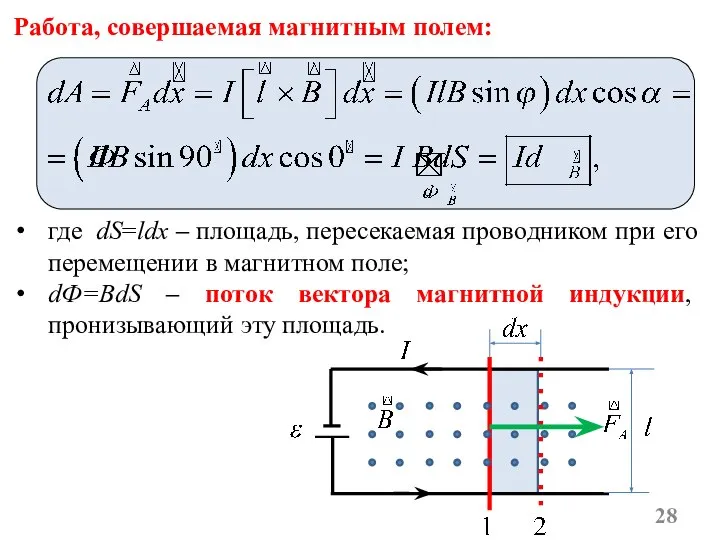
где dS=ldx – площадь, пересекаемая проводником при его перемещении в магнитном поле;
dФ=BdS – поток вектора магнитной индукции, пронизывающий эту площадь.
Работа, совершаемая магнитным полем:

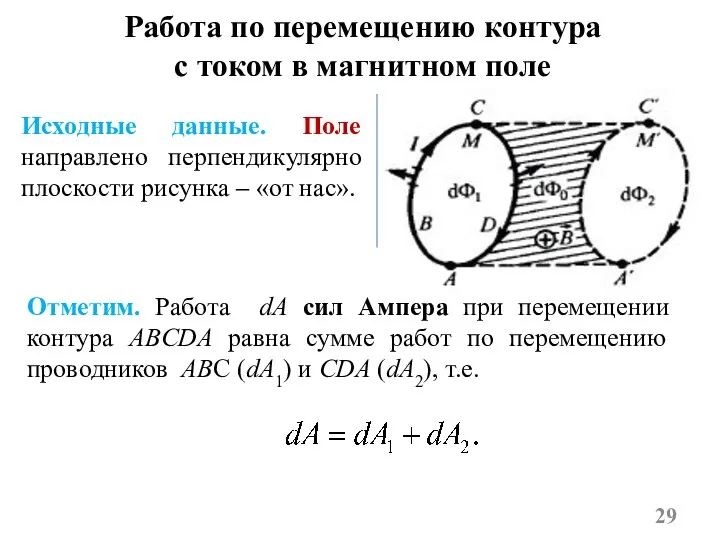
Работа по перемещению контура
с током в магнитном поле
Отметим. Работа dA сил Ампера при перемещении контура ABCDA равна сумме работ по перемещению проводников ABC (dA1) и CDA (dA2), т.е.
Исходные данные. Поле направлено перпендикулярно плоскости рисунка – «от нас».

Особенно важно. 1) При перемещении участка CDA силы Ампера направлены в сторону перемещения (образуют с направлением перемещения острые углы), поэтому dA2>0:
2) Силы, действующие на участок ABC контура, направлены против перемещения (образуют с направлением перемещения тупые углы), поэтому dA1<0:

В сумме
Работа по перемещению замкнутого контура с током в магнитном поле равна произведению силы тока в контуре на изменение магнитного потока, сцепленного с контуром.

Между полюсами сильного электромагнита помещается вакуумная камера, в которой находятся два электрода в виде полых металлических полуцилиндров (дуантов). К дуантам приложено переменное электрическое напряжение, частота которого равна циклотронной частоте. Заряженные частицы инжектируются в центре вакуумной камеры. Частицы ускоряются электрическим полем в промежутке между дуантами. Внутри дуантов частицы движутся под действием силы Лоренца по полуокружностям, радиус которых растет по мере увеличения энергии частиц. Каждый раз, когда частица пролетает через зазор между дуантами, она ускоряется электрическим полем. Таким образом, в циклотроне, как и во всех других ускорителях, заряженная частица ускоряется электрическим полем, а удерживается на траектории магнитным полем. Циклотроны позволяют ускорять протоны до энергии порядка 20 МэВ.
Однородные магнитные поля используются во многих приборах и, в частности, в масс-спектрометрах – устройствах, с помощью которых можно измерять массы заряженных частиц – ионов или ядер различных атомов. Масс-спектрометры используются для разделения изотопов, то есть ядер атомов с одинаковым зарядом, но разными массами (например, 20Ne и 22Ne). Простейший масс-спектрометр показан на рис. 1.18.4. Ионы, вылетающие из источника S, проходят через несколько небольших отверстий, формирующих узкий пучок. Затем они попадают в селектор скоростей, в котором частицы движутся в скрещенных однородных электрическом и магнитном полях. Электрическое поле создается между пластинами плоского конденсатора, магнитное поле – в зазоре между полюсами электромагнита. Начальная скорость заряженных частиц направлена перпендикулярно векторам и
На частицу, движущуюся в скрещенных электрическом и магнитном полях, действуют электрическая сила и магнитная сила Лоренца. При условии E = υB эти силы точно уравновешивают друг друга. Если это условие выполняется, частица будет двигаться равномерно и прямолинейно и, пролетев через конденсатор, пройдет через отверстие в экране. При заданных значениях электрического и магнитного полей селектор выделит частицы, движущиеся со скоростью υ = E / B.
Далее частицы с одним и тем же значением скорости попадают в камеру масс-спектрометра, в которой создано однородное магнитное поле Частицы движутся в камере в плоскости, перпендикулярной магнитному полю, под действием силы Лоренца. Траектории частиц представляют собой окружности радиусов R = mυ / qB'. Измеряя радиусы траекторий при известных значениях υ и B' можно определить отношение q / m. В случае изотопов (q1 = q2) масс-спектрометр позволяет разделить частицы с разными массами.
Современные масс-спектрометры позволяют измерять массы заряженных частиц с точностью выше 10–4.

Быстрые заряженные частицы из космоса (главным образом от Солнца) «захватываются» магнитным полем Земли и образуют так называемые радиационные пояса, в которых частицы, как в магнитных ловушках, перемещаются туда и обратно по спиралеобразным траекториям между северным и южным магнитными полюсами за времена порядка долей секунды. Лишь в полярных областях некоторая часть частиц вторгается в верхние слои атмосферы, вызывая полярные сияния.

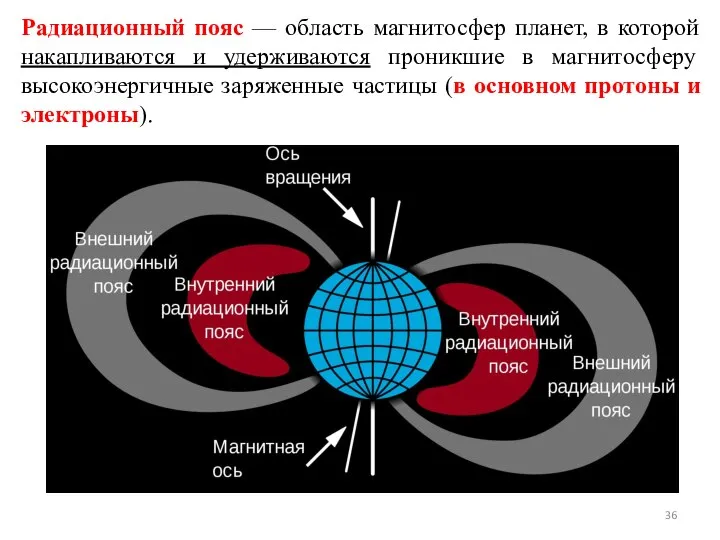
Радиационный пояс — область магнитосфер планет, в которой накапливаются и удерживаются проникшие в магнитосферу высокоэнергичные заряженные частицы (в основном протоны и электроны).

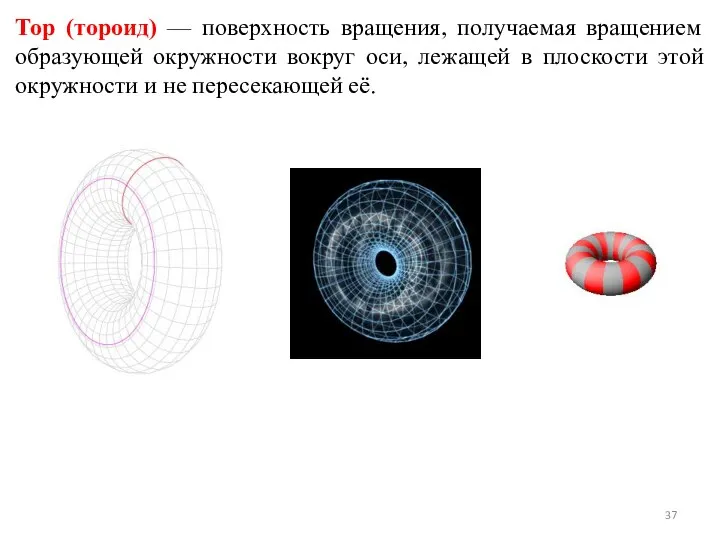
Тор (тороид) — поверхность вращения, получаемая вращением образующей окружности вокруг оси, лежащей в плоскости этой окружности и не пересекающей её.

Радиационный пояс в первом приближении представляет собой тороид, в котором выделяются две области:
внутренний радиационный пояс на высоте ≈ 4000 км, состоящий преимущественно из протонов с энергией в десятки МэВ;
внешний радиационный пояс на высоте ≈ 17 000 км, состоящий преимущественно из электронов с энергией в десятки кэВ.
Между внутренним и внешним радиационными поясами имеется щель, расположенная в интервале от 2 до 3 радиусов Земли.
Потоки частиц во внешнем поясе больше, чем во внутреннем.

Полярное сияние (авро́ра, лат. Aurora) — свечение (люминесценция) верхних слоёв атмосфер планет, обладающих магнитосферой, вследствие их взаимодействия с заряженными частицами солнечного ветра.
Солнечный ветер — поток ионизированных частиц (в основном гелиево-водородной плазмы), истекающий из солнечной короны со скоростью 300—1200 км/с в окружающее космическое пространство. Является одним из основных компонентов межпланетной среды.

При столкновении энергичных частиц плазменного слоя с верхней атмосферой происходит возбуждение атомов и молекул газов, входящих в её состав.
Излучение возбуждённых атомов в видимом диапазоне и наблюдается как полярное сияние.
Спектры полярных сияний зависят от состава атмосфер планет.
Для Земли наиболее яркими являются линии излучения возбуждённых атомов кислорода и азота в видимом диапазоне;
Для Юпитера — линии излучения водорода в ультрафиолете.
Красное свечение кислорода наблюдается на высотах 200 — 400 км, а совместное свечение азота и кислорода — на высоте ~110км.

Газовый разряд — совокупность процессов, возникающих при протекании электрического тока через вещество, находящееся в газообразном состоянии.
Обычно протекание тока становится возможным только после достаточной ионизации газа и образования плазмы.
Ионизация может происходить в результате
столкновений электронов, ускорившихся в электромагнитном поле, с атомами газа.
При этом возникает лавинное увеличение числа заряженных частиц, поскольку в процессе ионизации образуются новые электроны, которые тоже после ускорения начинают участвовать в соударениях с атомами, вызывая их ионизацию.
электрическое поле высокой напряжённости (искровой разряд) или
высокая температура (дуговой разряд).

Для возникновения и поддержания газового разряда требуется
существование электрического поля или
переменного магнитного поля,
так как плазма может существовать только если электроны приобретают во внешнем поле энергию, достаточную для ионизации атомов, и количество образованных ионов превышает число рекомбинировавших ионов.
Если для существования газового разряда необходима дополнительная ионизация за счёт внешних источников (например, при помощи ионизирующих излучений), то газовый разряд называется несамостоятельным.
Для осуществления газового разряда применяют как постоянные во времени, так и переменные электрические и магнитные поля.

Цвета тлеющих разрядов в различных газах