Содержание
- 2. ДИНАМИКА, СТАТИКА Динамика материальной точки Динамика системы материальных точек Динамика абсолютно твердого тела
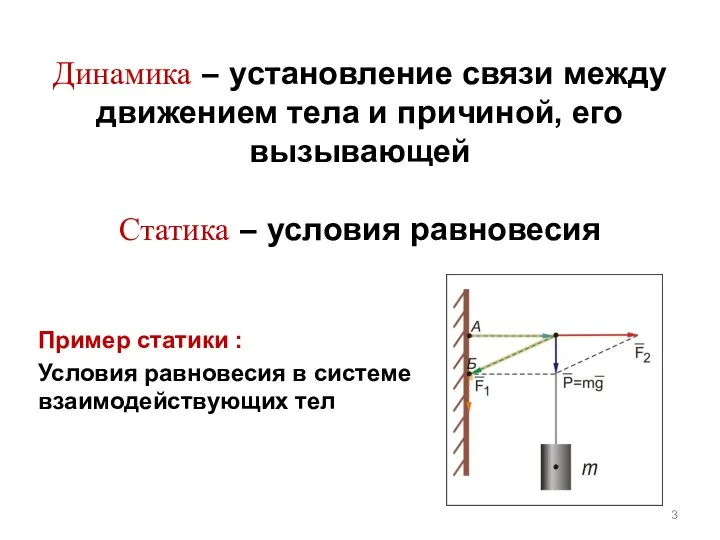
- 3. Динамика – установление связи между движением тела и причиной, его вызывающей Статика – условия равновесия Пример
- 4. Законы динамики (законы Ньютона) I закон: Всякое тело находится в состоянии покоя или равномерного прямолинейного движения
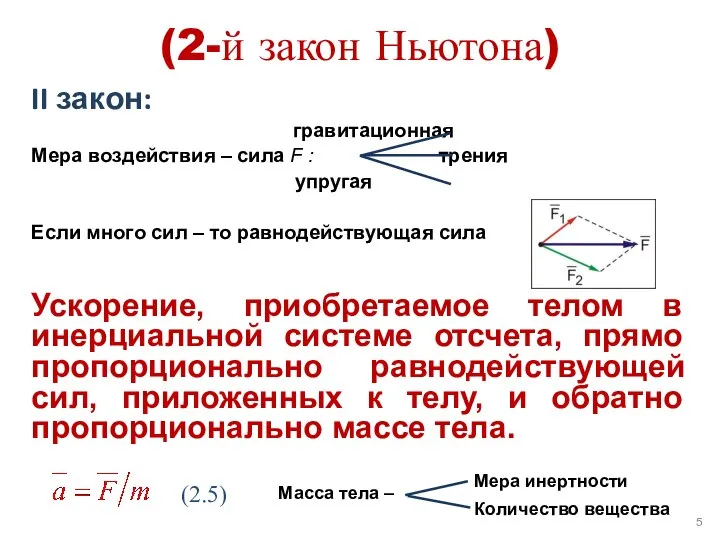
- 5. (2-й закон Ньютона) II закон: гравитационная Мера воздействия – сила F : трения упругая Если много
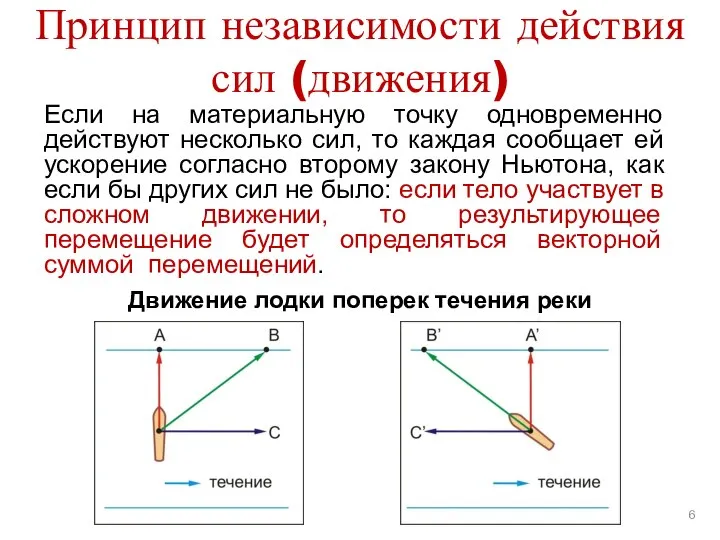
- 6. Принцип независимости действия сил (движения) Если на материальную точку одновременно действуют несколько сил, то каждая сообщает
- 7. Система единиц Формула размерности Единица измерения величины А – условно выбранная величина, имеющая тот же смысл,
- 8. Система единиц: СИ, СГС Основные единицы : длина l, [L] : м см время t, [T]
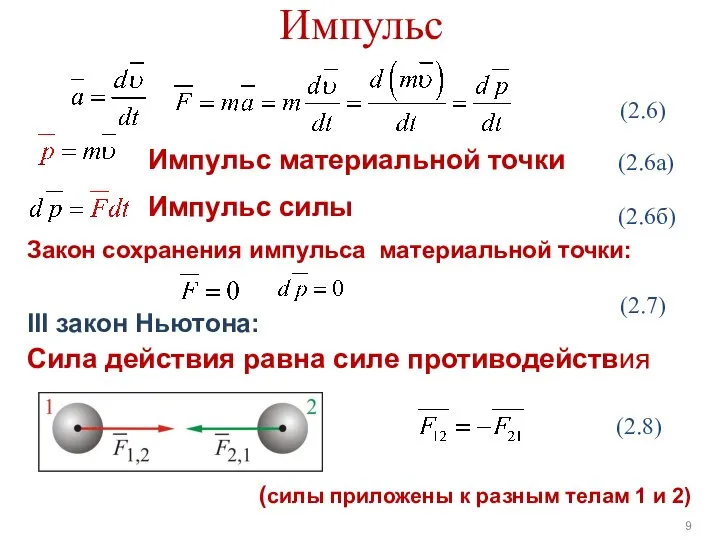
- 9. Импульс Импульс материальной точки Закон сохранения импульса материальной точки: III закон Ньютона: Сила действия равна силе
- 10. Динамика системы материальных точек или скорость перемещения центра масс (инерции) (2.9) (2.10) (2.10а) координата центра инерции
- 11. Уравнение движения системы материальных точек или твердого тела Центр инерции (масс, тяжести) движется так, как двигалась
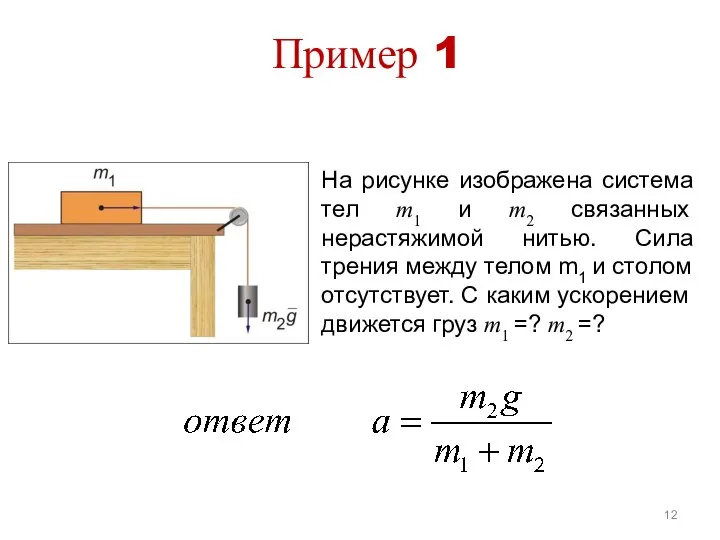
- 12. Пример 1 На рисунке изображена система тел m1 и m2 связанных нерастяжимой нитью. Сила трения между
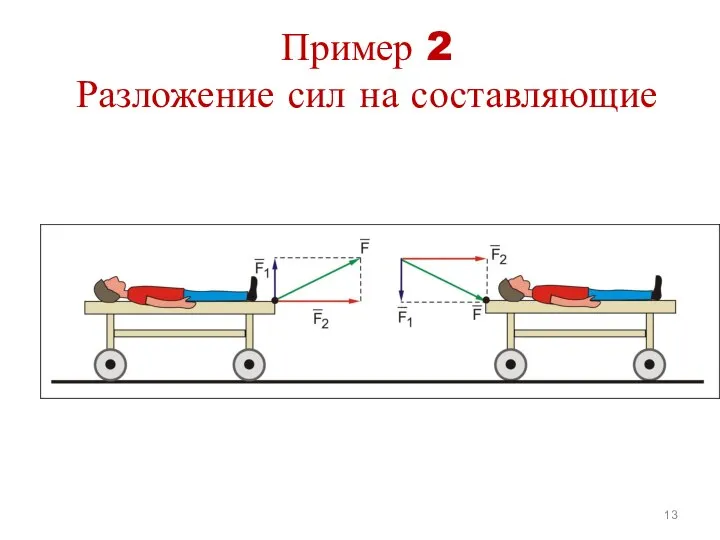
- 13. Пример 2 Разложение сил на составляющие
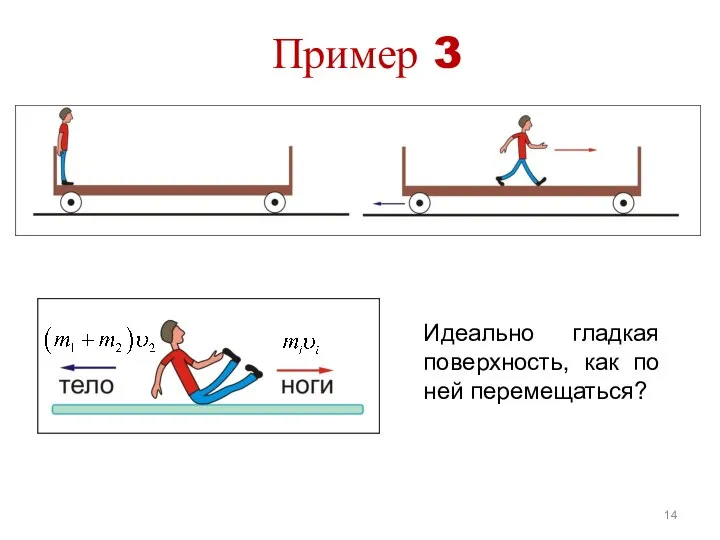
- 14. Пример 3 Идеально гладкая поверхность, как по ней перемещаться?
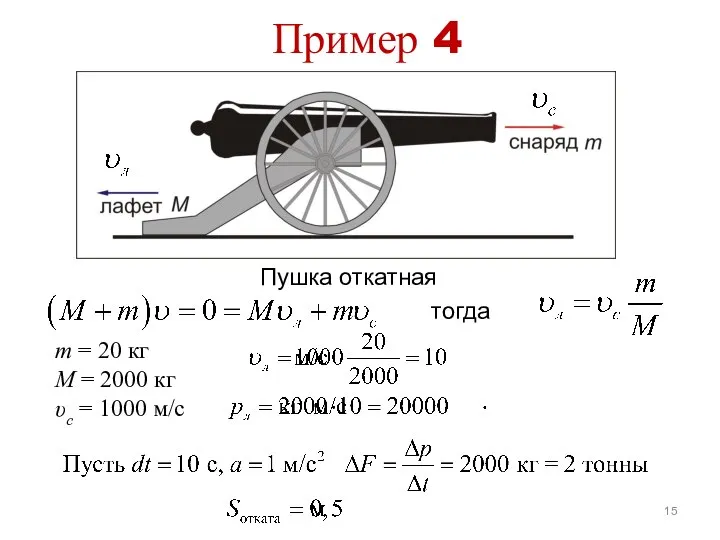
- 15. Пример 4 тогда Пушка откатная m = 20 кг M = 2000 кг υc = 1000
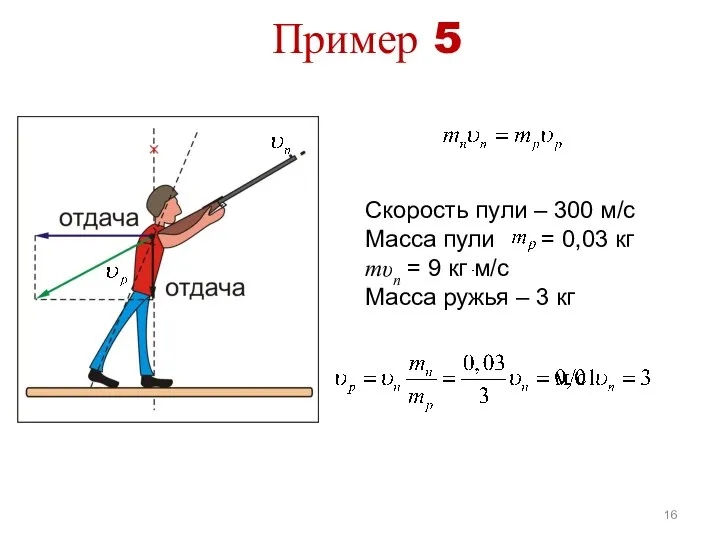
- 16. Пример 5 Скорость пули – 300 м/с Масса пули = 0,03 кг mυп = 9 кг
- 18. Скачать презентацию



![Система единиц: СИ, СГС Основные единицы : длина l, [L] : м](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/963094/slide-7.jpg)


 Законы сохранения в механике. Решение задач
Законы сохранения в механике. Решение задач Особенности конструкции элементов системы неавтоматического управления
Особенности конструкции элементов системы неавтоматического управления Расчёт массы и объёма тела по его плотности. 7 класс
Расчёт массы и объёма тела по его плотности. 7 класс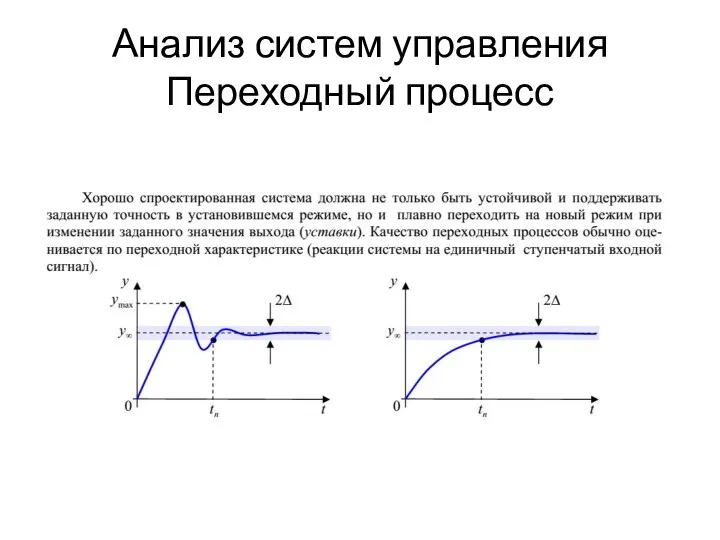 Анализ систем управления. Переходный процесс. ТАУ 5
Анализ систем управления. Переходный процесс. ТАУ 5 Как устроен атом
Как устроен атом В.А. Грибов. Я сдам ЕГЭ. Физика
В.А. Грибов. Я сдам ЕГЭ. Физика Порівняння роботи рухомого складу за різними видами тяги
Порівняння роботи рухомого складу за різними видами тяги Определение массы небесных тел
Определение массы небесных тел Презентация на тему Трение в природе и технике
Презентация на тему Трение в природе и технике 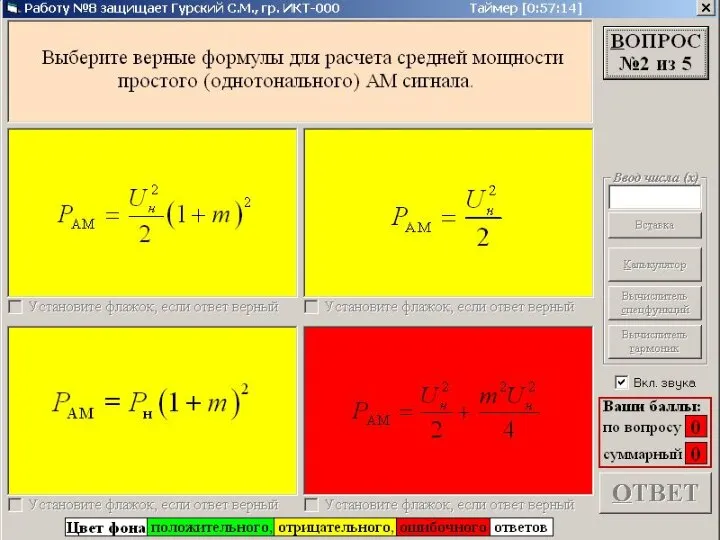 АМ БМ ОМ - математические модели сигналов. Тест
АМ БМ ОМ - математические модели сигналов. Тест Презентация на тему Сила упругости. Закон Гука. Вес тела
Презентация на тему Сила упругости. Закон Гука. Вес тела  Теорема Гаусса
Теорема Гаусса Реконструкция установки производства фталевого ангидрида
Реконструкция установки производства фталевого ангидрида Airbus 320 A. C.T. (Airbus Competence Training)
Airbus 320 A. C.T. (Airbus Competence Training) Электромагнитные излучения
Электромагнитные излучения Последовательное соединение
Последовательное соединение Парадоксы квантовой механики. Вселенная как она есть: Бог, время, человек
Парадоксы квантовой механики. Вселенная как она есть: Бог, время, человек Исследовательская работа на тему: Изучение плотности веществ
Исследовательская работа на тему: Изучение плотности веществ Простые механизмы
Простые механизмы Спектрометрия ультрафиолетовой и видимой части спектра
Спектрометрия ультрафиолетовой и видимой части спектра Сила тяжести. Сила упругости. Вес тела
Сила тяжести. Сила упругости. Вес тела Магнитное поле электрического тока
Магнитное поле электрического тока Бином Ньютона. 11 класс
Бином Ньютона. 11 класс Удельная теплоемкость
Удельная теплоемкость LT-система физических единиц
LT-система физических единиц Характеристики катера Амур-М
Характеристики катера Амур-М Цепная передача
Цепная передача Динамика судна. Общие понятия гидромеханики
Динамика судна. Общие понятия гидромеханики