Теоретические основы электротехники. Теория электромагнитного поля. Лекция 8

Векторный потенциал магнитного поля
Векторный потенциал - вспомогательная величина, с помощью которой можно анализировать магнитные поля постоянных токов, как вне проводников с токами, так и внутри этих проводников.
Второе уравнение будет выполняться всегда, если представить вектор магнитной индукции, как ротор некоторого вспомогательного вектора
- векторный потенциал магнитного поля.

Наложим на векторный потенциал такие условия, чтобы при подстановке его в уравнения магнитного поля эти уравнения выполнялись бы во всех точках поля – как при
так и при
В этом случае векторным магнитным потенциалом можно будет пользоваться для анализа магнитных полей в любых средах.
так как именно на этом основании мы ввели векторный потенциал.
Принцип непрерывности магнитного потока выполняется всегда, так как именно на этом основании мы ввели векторный потенциал

μ(x,y,z) = const
Подставим векторный потенциал в закон полного тока при условии , что
Преобразуем левую часть уравнения, применяя формулу для двойного векторного произведения:

При рассмотрении магнитного поля постоянных токов примем, что дивергенция векторного магнитного потенциала равна нулю:
Во всех точках магнитного поля постоянного тока выполняется принцип непрерывности линий векторного магнитного потенциала,
т. е. эти линии не имеют ни начала, ни конца и являются замкнутыми на себя кривыми.
A1n = A2n
Граничные условия на поверхности раздела двух сред:

Уравнение Пуассона для векторного потенциала

Для проекций векторов на оси координат, в частности для декартовой системы можем записать:
Уравнение Пуассона для скалярного электрического потенциала:
Одно уравнение переходит в другое при замене:
Уравнение Пуассона для векторного потенциала:

Решение уравнения Пуассона для скалярного электрического потенциала :
Решения уравнения Пуассона для проекций векторного потенциала:
Просуммировав умноженные на орты проекции векторного потенциала, получим решение уравнения Пуассона для векторного потенциала магнитного поля (под интегралом геометрическое суммирование):
Интегрирование проводится по всей области (объему), где плотность тока не равна нулю.

Случай линейных проводников с током.
Проводники считаются линейными, когда размеры поперечного сечения проводника намного меньше его длины
r
dv
l
Если направления векторов и
совпадают, а ток сквозь любое сечение проводника одинаков:
Если магнитное поле создано несколькими проводниками с токами, то следует интегрировать вдоль всех проводников с токами, тогда:

Все полученные соотношения для определения векторного потенциала справедливы в предположении, что в магнитном отношении среда однородна μ = const ≠ f(x,y,z) или кусочно - однородна.
Если среда неоднородна, то нельзя выносить μ за оператор ротора:

Определение магнитного потока через векторный потенциал
l
S
Применим теорему Стокса:

Граничные условия для векторного потенциала
A1τ = A2τ
На поверхностях раздела различных сред не изменяются ни нормальные, ни касательные составляющие векторного магнитного потенциала. Это означает, что при переходе из одной среды в другую векторный магнитный потенциал не изменяется ни по величине, ни по направлению.
При рассмотрении граничных условий из интегралов по замкнутым контурам для векторов поля мы получали на поверхности раздела сред равенство касательных составляющих векторов. По аналогии можем записать:

Пример
Определим магнитный поток, сцепляющийся с прямоугольной рамкой, расположенной в одной плоскости с прямолинейным проводником с током, причем две стороны рамки параллельны проводнику с током
i
– L
a
b
l
h
0
dz
+ L
z
r1
r2
A1
A2
Ak

Простота вычисления магнитных потоков с помощью векторного потенциала позволяет успешно использовать векторный магнитный потенциал для расчета собственных и взаимных индуктивностей

Расчет индуктивностей.
Общие выражения для взаимной и собственной индуктивностей
Выражения для индуктивностей будем получать в предположении, что в проводниках протекают равномерно распределенные по сечению постоянные токи. Предварительно введем понятие о внешнем и внутреннем магнитном потоке
Часть трубок магнитного потока (1 – 6), сцепленных с витком, не проходит сквозь проводник с током, а поток, созданный этими трубками называется внешним магнитным потоком. Трубки магнитного потока, проходящие сквозь материал проводника, сцепляются только с частью тока в проводнике и создают магнитный поток, называемый внутренним магнитным потоком.
1
2
3
4
5
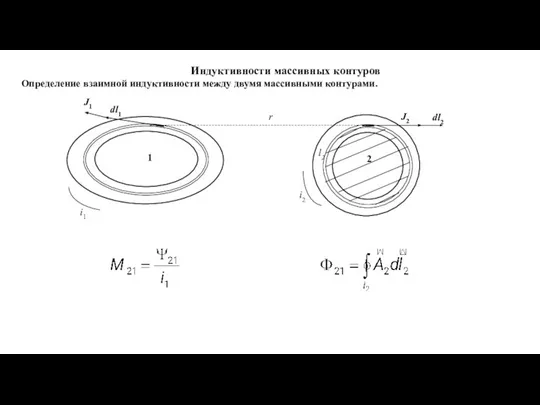
6

Индуктивности массивных контуров
Определение взаимной индуктивности между двумя массивными контурами.
r
dl1
J1
i1
i2
J2
dl2
1
2
l2

Элементарное потокосцепление с трубкой тока во втором контуре определяется отношением тока в этой трубке к полному току второго контура:
Полное потокосцепление взаимоиндукции второго контура получим, проинтегрировав полученное выражение по всем трубкам тока во втором контуре, т.е. всему объему второго контура:
Величина векторного магнитного потенциала в точках второго контура определяется с помощью полученного ранее решения уравнения Пуассона для векторного магнитного потенциала через плотность тока в первом контуре:

Тогда потокосцепление взаимоиндукции второго контура можем представить в виде:
Взаимная индуктивность между вторым и первым контуром можно вычислить из соотношения:
При определении взаимной индуктивности между первым и вторым контуром необходимо определить потокосцепление первого контура, задав ток во втором контуре. Проделав аналогичные вычисления, получим: