Содержание
- 6. Задача 6 В отделе работают 41 человек, из которых каждый знает хотя бы один иностранный язык.
- 7. Проверка 1) 6+3=9 – только английский 2) 5+3=8- только немецкий 3) 4+3=7 – только французский 9+8+7+5+5+4+3
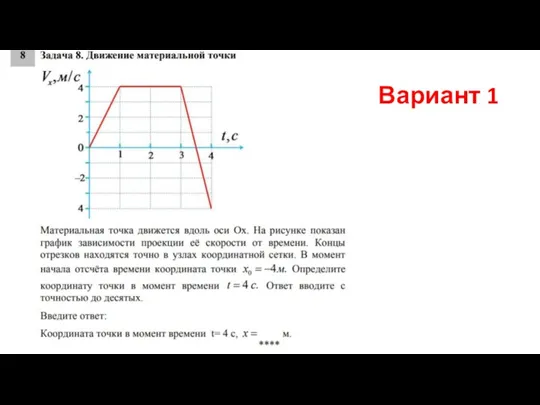
- 8. Вариант 1
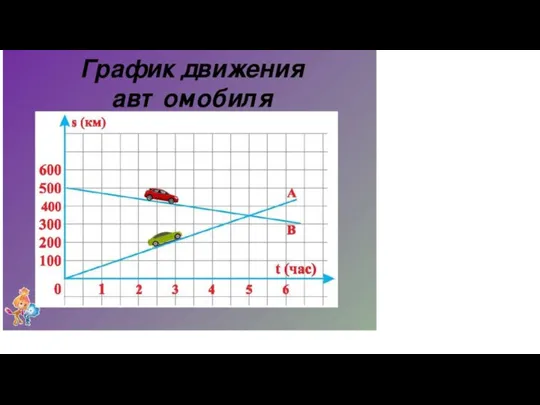
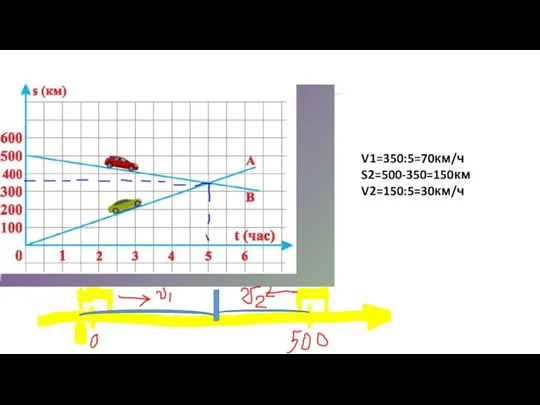
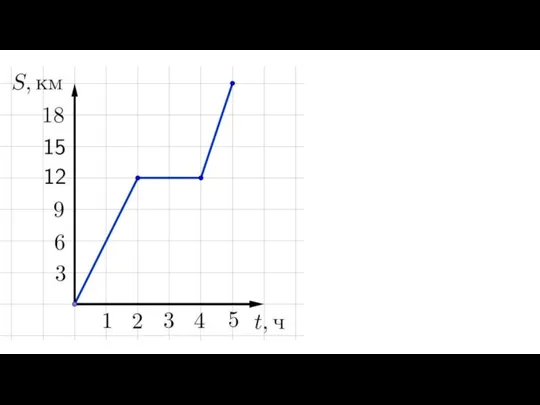
- 10. V1=350:5=70км/ч S2=500-350=150км V2=150:5=30км/ч
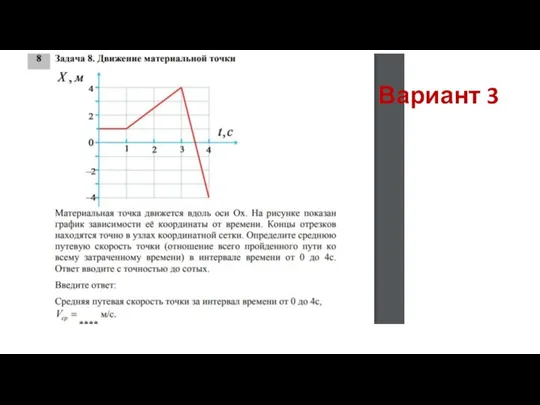
- 11. Вариант 3
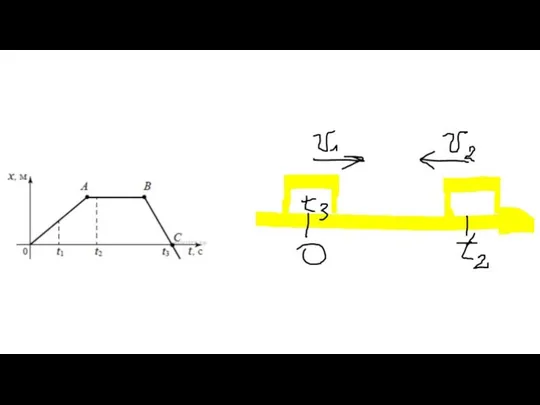
- 14. Задача 4
- 15. F=P-Fa, Fa=2/3P
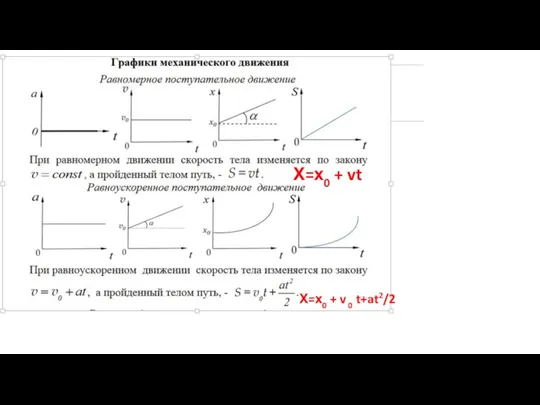
- 20. Х=х0 + vt Х=х0 + v 0 t+at2/2
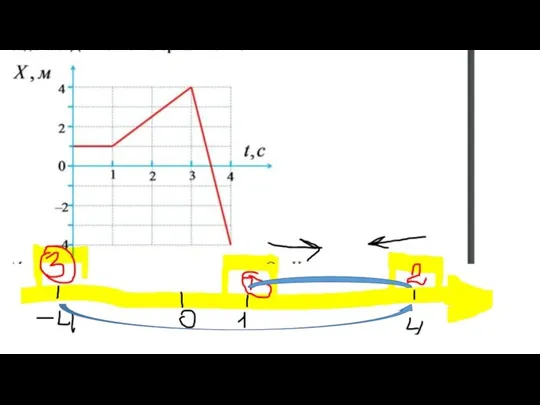
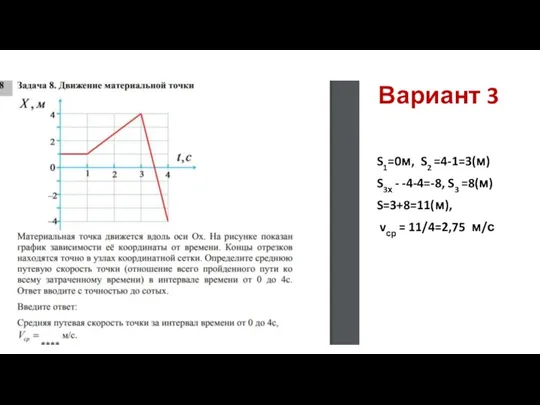
- 21. Вариант 3 S1=0м, S2 =4-1=3(м) S3х - -4-4=-8, S3 =8(м) S=3+8=11(м), vср = 11/4=2,75 м/с
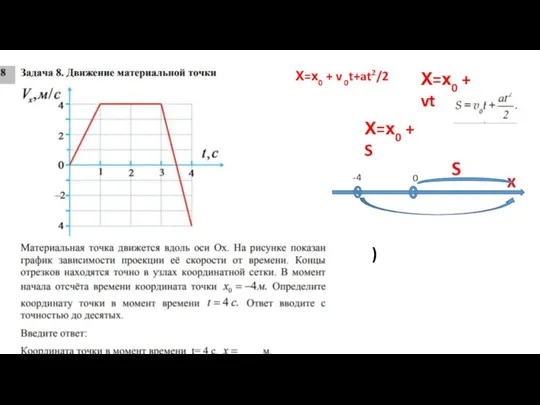
- 22. -4 0 Х=х0 + v 0t+at2/2 Х=х0 + vt Х=х0 + S x S )
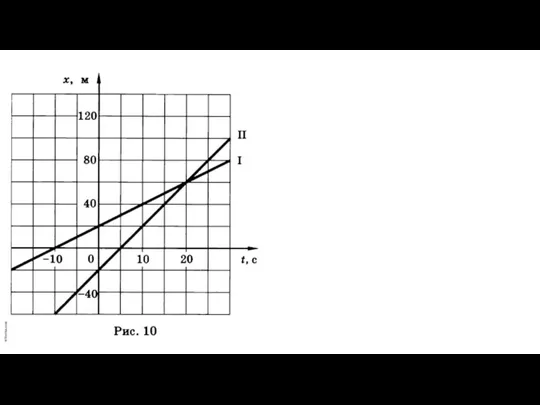
- 23. 12м/с 1100м 8м/с 1)V21=20м/с 10м/с t=1100/20=55© время тренера V12 =10-8=2 м/с 2●55=110 м
- 24. T+ Fa =Ft Fa = Ft - T, Fa=6Н-4,75Н=1,25Н Fa= ΔР M2 =5,275+0,125= =5,4кг
- 25. Задача 5 – 1 вариант Метод перебора. Применительно к неравенствам с модулем выглядит он так: Выписать
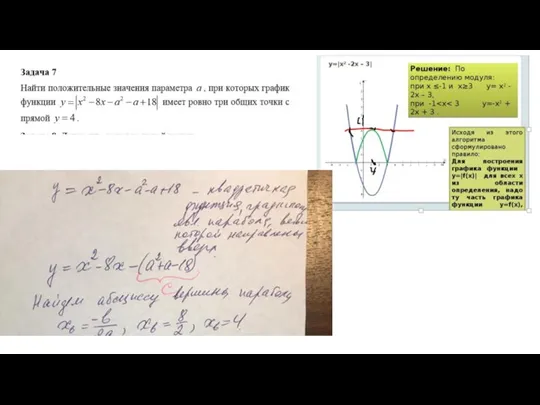
- 26. Задача 5 - 3 вариант Неравенства с модулем. Метод перебора. Применительно к неравенствам с модулем выглядит
- 27. Задача5 Выпишем все подмодульные выражения и приравняем их к нулю: Х-1=0, х+2=0 х=1 и х=-2 Итого
- 28. 2) Таким образом, получаем [-0,25; 0) -0,25 0
- 29. Т.к. 5>0, то х-4>0, х>4 Т.е. (4; ∞) решение неравенства на третьем интервале. Объединяя все случаи,
- 30. Преобразование иррациональных выражений
- 33. Дано m=1,5кг t= 00 λ =3,3*105 Дж/кг r= 2,3*106 Дж/ кг Найти –х, часть испарившейся воды
- 34. X=0,125(m-y) или 8х=(m-y) Х – в 8 раз меньше, чем испарится и замерзнет, т.е. испарится в
- 35. Задача 10
- 39. Скачать презентацию
























 Метрология. Измерение электрической мощности. Точность измерений
Метрология. Измерение электрической мощности. Точность измерений Статические методы определения твердости
Статические методы определения твердости Презентация на тему Цепная реакция деления ядер урана
Презентация на тему Цепная реакция деления ядер урана  Эффект Доплера
Эффект Доплера Механические колебания
Механические колебания Специзмерения системах автоматики и телемеханики
Специзмерения системах автоматики и телемеханики Динамика материальной точки (частицы)
Динамика материальной точки (частицы) Гибридно-волновой движитель
Гибридно-волновой движитель Невагомiсть
Невагомiсть Пара сил и момент силы относительно точки
Пара сил и момент силы относительно точки Механические волны
Механические волны Свойство волн
Свойство волн Сила трения. Опыт №1. Наблюдение явления трения
Сила трения. Опыт №1. Наблюдение явления трения Балочные системы. Определение реакций опор. (Тема 1.4.1)
Балочные системы. Определение реакций опор. (Тема 1.4.1) Обледенение летательных аппаратов
Обледенение летательных аппаратов Наблюдение сплошного и линейчатых спектров. Лабораторная работа
Наблюдение сплошного и линейчатых спектров. Лабораторная работа Расчет давления в жидкости
Расчет давления в жидкости Назначение основных размеров опор и определение нагрузок, действующих на опоры
Назначение основных размеров опор и определение нагрузок, действующих на опоры Примеры физических явлений
Примеры физических явлений Основные определения
Основные определения Показатели регулирования САУ
Показатели регулирования САУ Давление в жидкости и газе
Давление в жидкости и газе Вимушені коливання. Резонанс (Лекція 4)
Вимушені коливання. Резонанс (Лекція 4) Область исследования цвета и света
Область исследования цвета и света prez_L3
prez_L3 Расчёт пути и времени движения. Физика, 7 класс
Расчёт пути и времени движения. Физика, 7 класс Новая жизнь полной интегрируемости 2
Новая жизнь полной интегрируемости 2 Электричество и магнетизм магнитное поле
Электричество и магнетизм магнитное поле