Движение по окружности

Изучить основные характеристики движения:
угловая скорость;
линейная скорость;
ускорение;
период.
Рассмотреть всевозможные случаи применения движения по окружности:
вращение тела;
движение на поворотах;
движение планет;
движение заряженных частиц.
Цели

Линейная скорость, v (м/с).
Угловая скорость, ω (рад/с).
Центростремительное ускорение, а (м/с²).
Период обращения, Т (с).
Частота обращения, ν (рад/с).
Характеристики движения

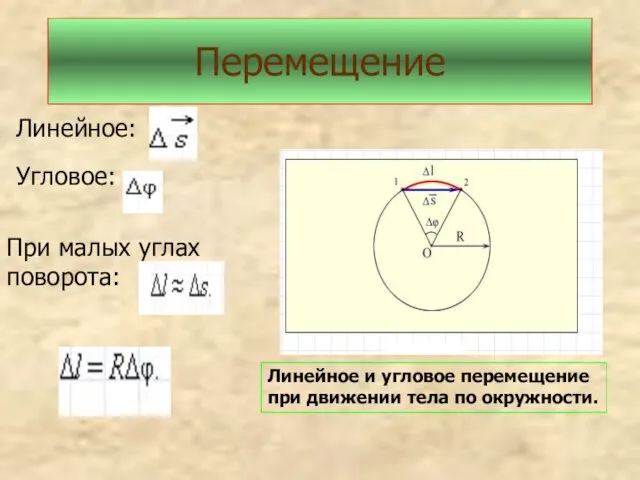
Перемещение
Линейное:
Угловое:
При малых углах
поворота:
Линейное и угловое перемещение
при движении тела по окружности.

Траектория движения

Скорость
Линейная скорость
Угловая скорость
V=s/t
ω=ϕ/t
Модель.Модель. Модель. Скорость тела при движении по Модель. Скорость тела при движении по Модель. Скорость тела при движении по окружности.
V=R

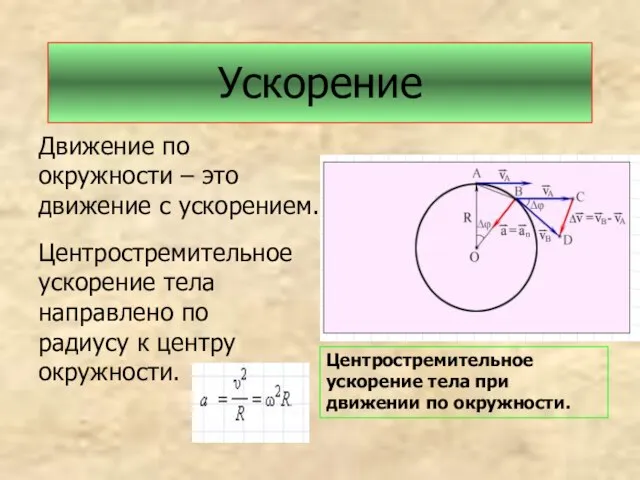
Ускорение
Движение по окружности – это движение с ускорением.
Центростремительное ускорение тела направлено по радиусу к центру окружности.
Центростремительное ускорение тела при движении по окружности.

Тангенциальное ускорение
Ускорение тела при неравномерном движении по окружности.
При неравномерном движении тела:
Тангенциальное ускорение тела:

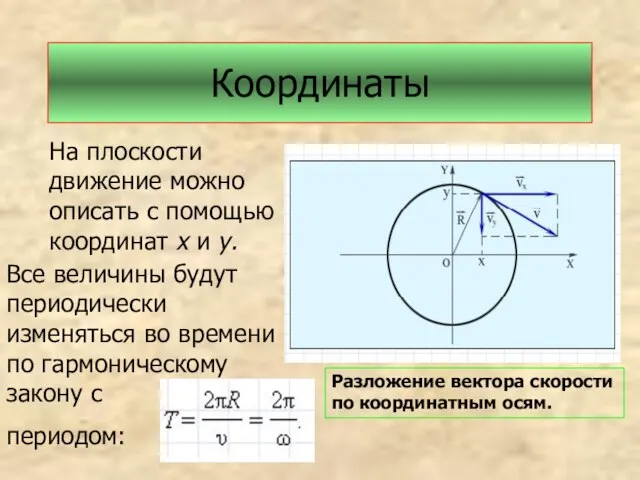
Координаты
На плоскости движение можно описать с помощью координат х и у.
Все величины будут периодически изменяться во времени по гармоническому закону с
периодом:
Разложение вектора скорости по координатным осям.

Условие движения
Для движения тела по окружности необходимо, чтобы на это тело действовала сила, направленная к центру окружности и равная:
F=mv²/r или F=m²r.
F
F

Вращение шара в вертикальной плоскости
Центростремительное ускорение вызывается равнодействующей сил упругости и тяжести.
В нижней точке: R= Fупр-mg,
направлена вверх.
В верхней точке: R=Fупр+mg,
направлена вниз.
Модель.

Движение тела на поворотах
Центростремительное ускорение на поворотах дороги вызывает сила трения.
Для этого водитель автомобиля разворачивает рулем передние колеса.
Спортсмен наклоняет корпус в сторону центра поворота.
Fтр
а
Fтр
а
Fтр=mg=mv²/r,
μg=v²/r.

Движение тела на поворотах
При повороте равнодействующая всех сил должна быть направлена к центру поворота.
Для этого на скоростных трассах делают наклон дороги.
У самолета на хвостовом оперении есть руль поворота.
mg
a
N
R
F
mg
R
a
R=mv²/r.

Движение тел в гравитационном поле
Сила гравитационного притяжения сообщает и небесным телам центростремительное ускорение.
Траектории:
1-круговая;
2,3 –эллиптические; 4-параболическая;
5-гиперболическая; 6- траектория Луны.
Модель.

Движение планет
Первый закон Кеплера. Орбита каждой планеты есть эллипс, в одном из фокусов (F) которого находится Солнце.
F,F-фокусы,
а – большая полуось,
Р-перигелий,
А-афелий.

Движение планет
Второй закон Кеплера. Радиус-вектор планеты в равные промежутки времени описывает равные площади.
Третий закон Кеплера.

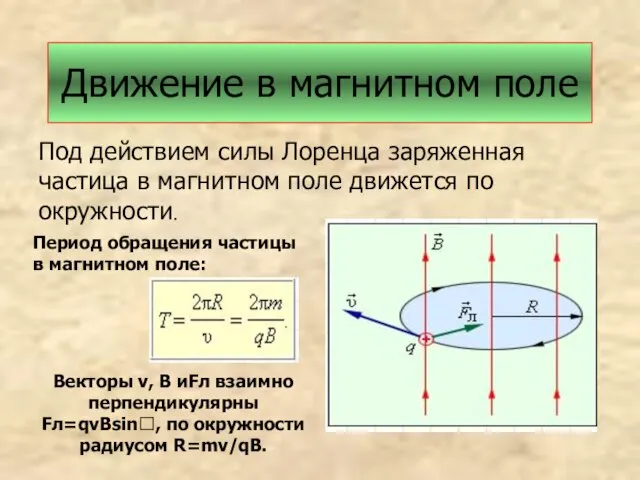
Движение в магнитном поле
Под действием силы Лоренца заряженная частица в магнитном поле движется по окружности.
Период обращения частицы в магнитном поле:
Векторы v, В иFл взаимно перпендикулярны Fл=qvBsin, по окружности радиусом R=mv/qB.

Радиационные пояса Земли
Поток заряженных частиц, влетая в магнитное поле Земли, под действием силы Лоренца начинает двигаться от одного полюса к другому и обратно.
Радиационные пояса – области, в которых находятся частицы задержанные магнитным полем.