Движение тела брошенного под углом к горизонту. Повторение, решение задач (10 класс)

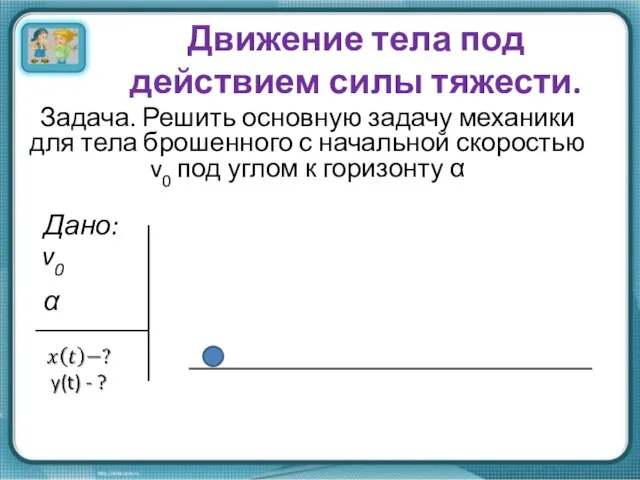
Движение тела под действием силы тяжести.
Задача. Решить основную задачу механики для тела брошенного с начальной скоростью v0 под углом к горизонту α
Дано:
v0
α

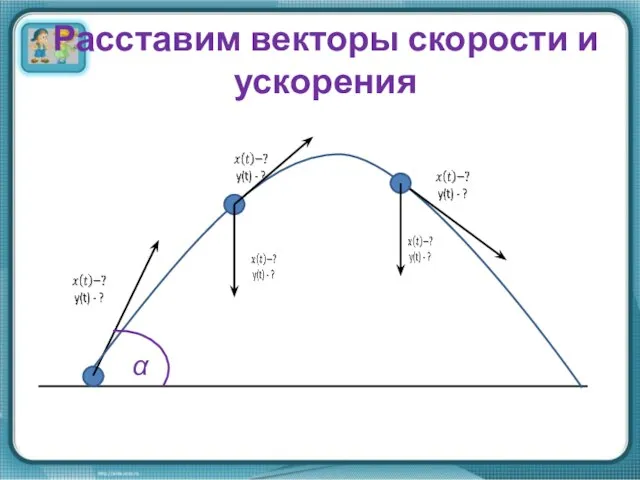
Расставим векторы скорости и ускорения
α

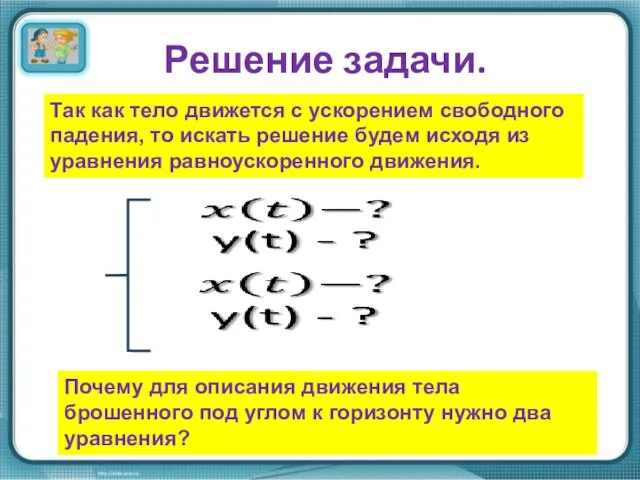
Решение задачи.
Так как тело движется с ускорением свободного падения, то искать решение будем исходя из уравнения равноускоренного движения.
Почему для описания движения тела брошенного под углом к горизонту нужно два уравнения?

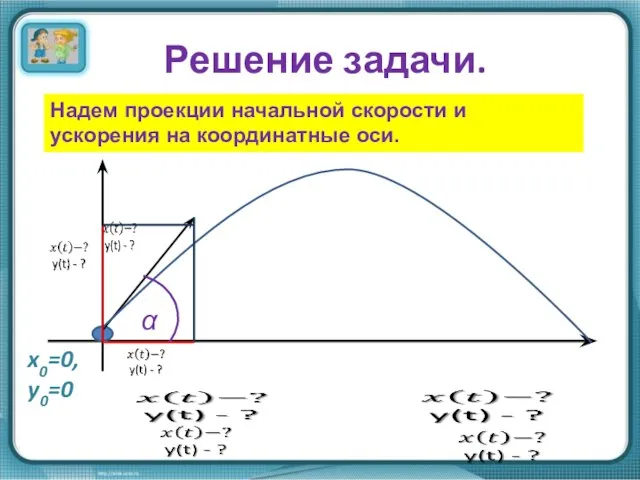
Решение задачи.
Надем проекции начальной скорости и ускорения на координатные оси.
α
x0=0, y0=0

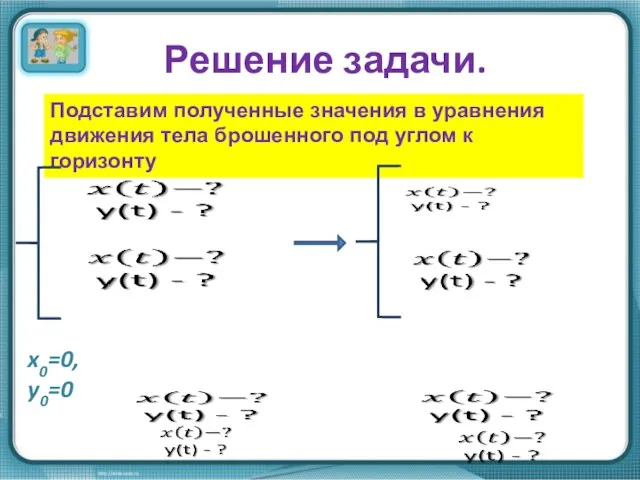
Решение задачи.
Подставим полученные значения в уравнения движения тела брошенного под углом к горизонту
x0=0, y0=0

1.Vy=V0 *sinα-gt
Время подъёма tпод(до точки А).
2.В точке А проекция скорости Vу на ось ОУ равна нулю при t=tпод : Vу=0 =>
3. 0=Vо*sinα-gtпод =>
4.gtпод =Vо*sinα =>
5.tпод =Vо*sinα/g

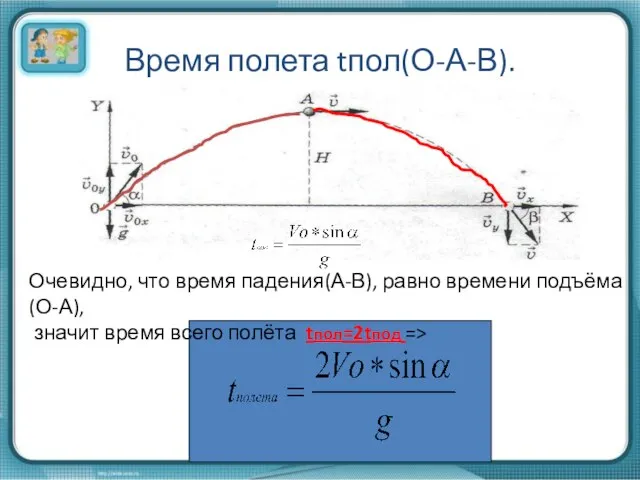
Время полета tпол(О-А-В).
Очевидно, что время падения(А-В), равно времени подъёма(О-А),
значит время всего полёта tпол=2tпод =>

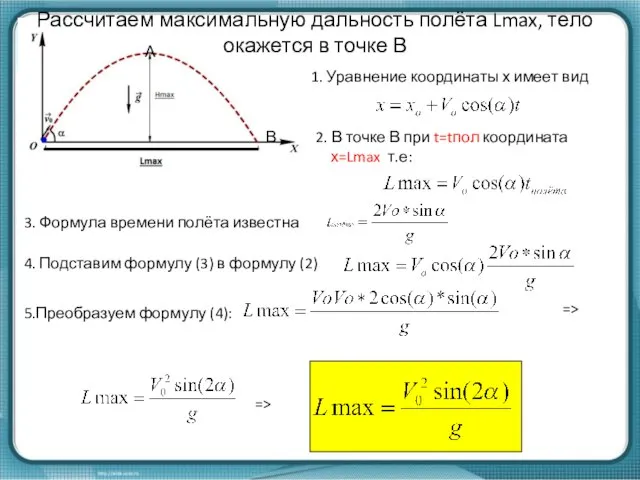
Рассчитаем максимальную дальность полёта Lmax, тело окажется в точке В
А
В
4. Подставим формулу (3) в формулу (2)
5.Преобразуем формулу (4):
2. В точке В при t=tпол координата
х=Lmax т.е:
1. Уравнение координаты х имеет вид
3. Формула времени полёта известна
=>
=>

Рассчитаем максимальную высоту подъёма Нmax
А
В
4. Подставим формулу (3) в формулу (2)
5.Преобразуем формулу (4):
2. В точке А при t=tпод координата
у=Нmax т.е:
1. Уравнение координаты у имеет вид
3. Формула времени подъёма известна
=>
=>

Задачи

Из окна дома с высоты 19,6 м горизонтально брошена монета со скоростью 5 м/с. Пренебрегая сопротивлением воздуха, найдите, через какой промежуток времени монета упадет на Землю На каком расстоянии по горизонтали от дома находится точка падения?

ответ:

2. Используя условие задачи 1, найдите скорость падения монеты и угол, который образует вектор скорости с горизонтом в точке падения

ответ:

3. Длина скачка блохи на столе, прыгающей под углом 45° к горизонту, равна 20 см. Во сколько раз высота ее подъема над столом превышает ее собственную длину, составляющую 0,4 мм?
рисунок.

ответ:

Мяч, брошенный под углом 45° к горизонту, упруго отскочив от вертикальной стены, расположенной на расстоянии L от точки бросания, ударяется о Землю на расстоянии l от стены С какой начальной скоростью был брошен мяч?

при абсолютно упругом ударе мяча о стенку модуль его скорости не изменяется, а угол падения равен углу отражения.
реальная траектория мяча является зеркальным отражением той траектории, по которой мяч летел бы в отсутствии стенки.
тогда из рисунка видно, что дальность полета мяча
4.

Спасибо за работу!
Домашнее задание
§ 16, Упр.4 (2, 3),
(Г.Я. Мякишев, Б.Б. Буховцев, Н.Н. Сотский Физика).
Спасибо за урок!