Конспект лекций по электротехнике

Преобразование электрических цепей

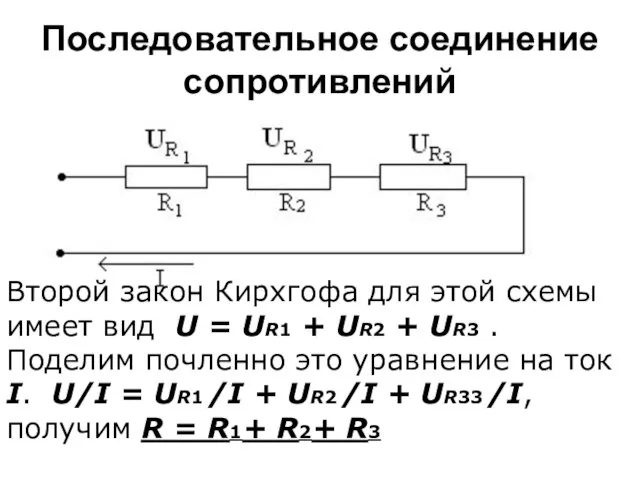
Последовательное соединение сопротивлений
Второй закон Кирхгофа для этой схемы имеет вид U = UR1 + UR2 + UR3 . Поделим почленно это уравнение на ток I. U/I = UR1 /I + UR2 /I + UR33 /I, получим R = R1+ R2+ R3

Последовательное соединение сопротивлений
Таким образом,
при последовательном соединении сопротивлений эквивалентное сопротивление равно сумме последовательно соединенных сопротивлений R, а эквивалентное сопротивление всегда получается больше наибольшего.

Параллельное соединение сопротивлений

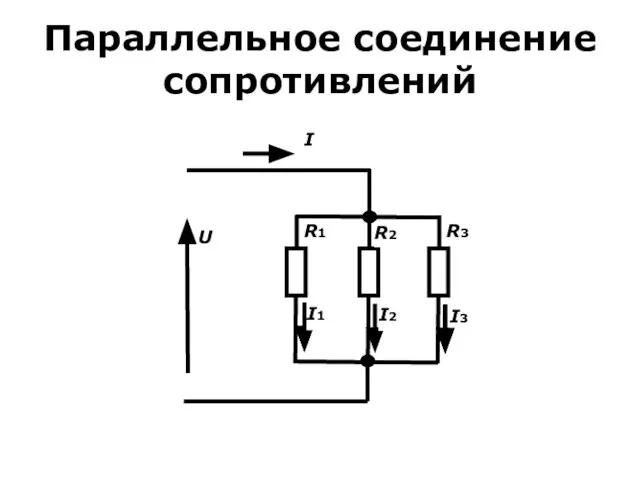
Параллельное соединение сопротивлений
Первый закон Кирхгофа для этой схемы выглядит так:
По закону Ома: I = U/Rэ ,
I1 = U/R1, I2 = U/R2 , I3 = U/R3.
Тогда: U/RЭ = U/R1+U/R2+U/R3 и
1/RЭ = 1/R1+1/R2+1/R3 ,
GЭ = G1+G2+G3.
I = I1+ I2 + I3 .

Параллельное соединение сопротивлений
Таким образом, при параллельном соединении сопротивлений эквивалентная проводимость равна сумме проводимостей, а выражение для эквивалентного сопротивления имеет вид:
RЭ = .
Эквивалентное сопротивление всегда получается меньше наименьшего.

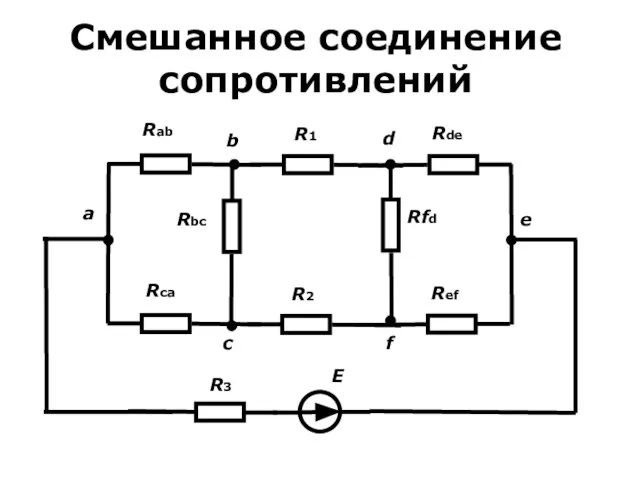
Смешанное соединение сопротивлений
Иногда нельзя определить параллельно или последовательно соединены сопротивления. Например, как показано на нижеприведенной схеме.

Смешанное соединение сопротивлений

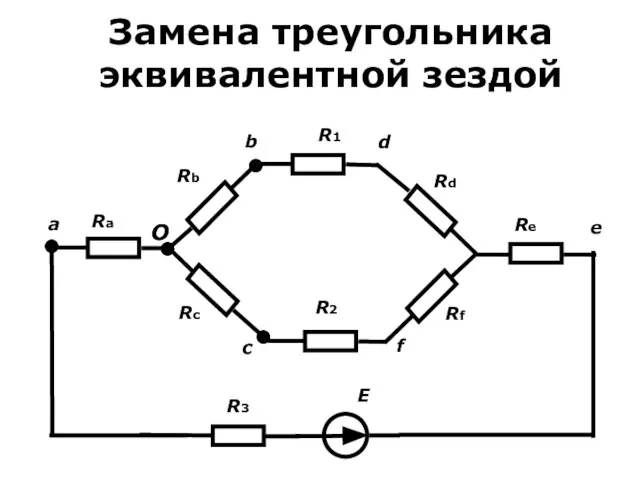
Смешанное соединение сопротивлений
В этом случае заменим треугольник abc звездой abc с соблюдением условия эквивалентности - так чтобы параметры (токи ветвей и межузловые напряжения) схемы вне преобразуемой цепи остались без изменения.

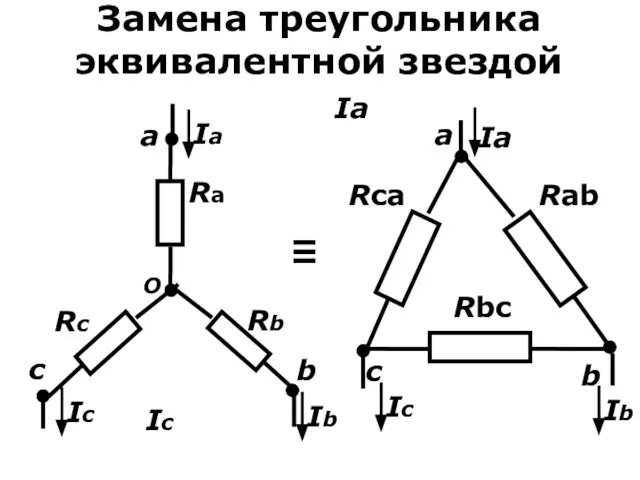
Замена треугольника эквивалентной зездой

Замена треугольника эквивалентной звездой
c
O
a
b
Ra
Rb
Rc
≡
a
b
c
Rab
Rbc
Rca
Ic
Ia

Замена треугольника эквивалентной звездой
Ia=0 Rb+Rc=Rbc⋅(Rab+Rca)/(Rab+Rbc+Rca) (1)
Ib=0 Ra+Rc=Rca⋅(Rab+Rbc)/(Rca+Rab+Rbc) (2)
Ic=0 Ra+Rb=Rab⋅(Rbc+Rca)/(Rab+Rbc+Rca) (3)
Решая систему относительно Ra, Rb, Rc . Находим их выражения

Замена треугольника эквивалентной звездой
Ra=Rab⋅Rca/(Rab+Rbc+Rca) (4)
Rb=Rbc⋅Rab/(Rca+Rab+Rbc) (5)
Rc=Rca⋅Rbc/(Rab+Rbc+Rca) (6)
Для замены звезды треугольником надо решить систему уравнений 4,5,6 относительно Rab, Rbc и Rсa:

Замена звезды эквивалентным треугольником
Rab=Ra+Rb+RaRb/Rc (7)
Rdc=Rb+Rc+RbRc/Ra (8)
Rca =Ra+Rc+RaRc/Ra (9)

Преобразование активных элементов

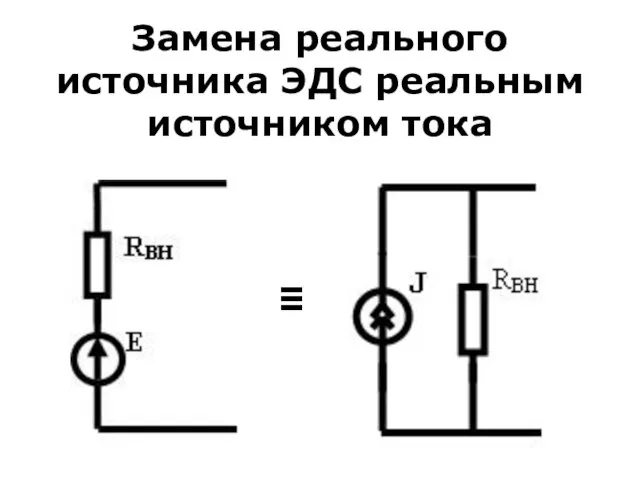
Замена реального источника ЭДС реальным источником тока
Источник ЭДС можно получить из источника тока, если последовательно с источником ЭДС (E = J*RBH) включить сопротивление, равное внутреннему сопротивлению источника тока. Соответственно значение тока источника тока определяют по формуле J = E/RВН.

Замена реального источника ЭДС реальным источником тока
≡

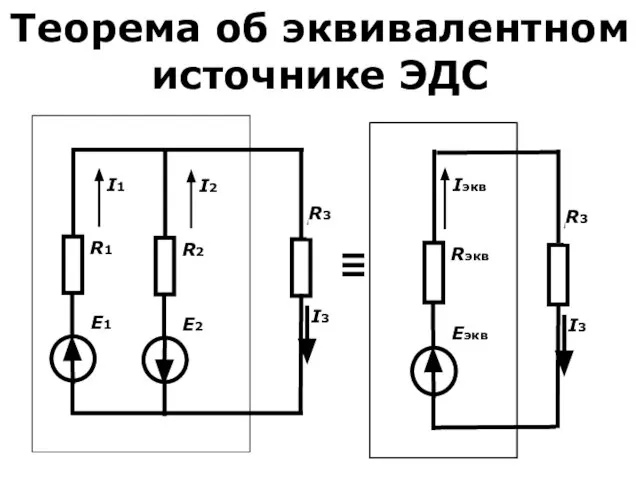
Теорема об эквивалентном источнике ЭДС
Теорема Гельмгольца – Те Ве Нена. - Активный двухполюсник по отношению к рассматриваемой цепи можно заменить эквивалентным источником напряжения, ЭДС которого равна напряжению холостого хода на зажимах этой ветви, а внутренне сопротивление равно входному сопротивлению двухполюсника.

Теорема об эквивалентном источнике ЭДС
≡

Теорема об эквивалентном источнике ЭДС
Eэк=(E1⋅G1 - E2⋅G2)/(G1+G2)=Uxx,
где G - проводимость, G=1/R
Rэкв = R1R2/(R1+R2)= Rвх12
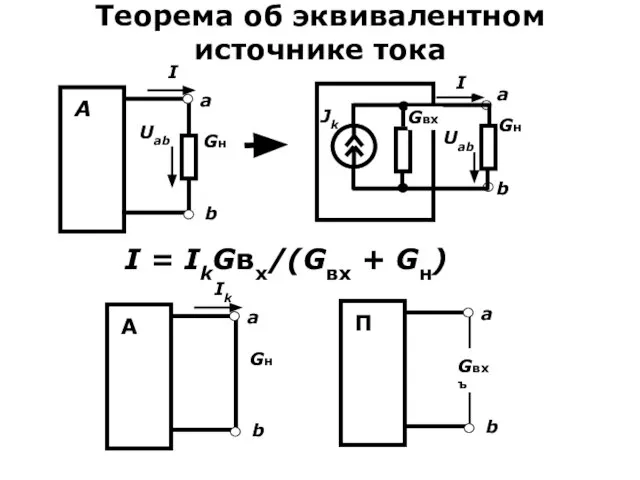
Iэк = I3 = Eэк/(Rэкв + R3)

Теорема об эквивалентном источнике тока
Теорема Нортона.
Активный двухполюсник по отношению к рассматриваемой ветви можно заменить эквивалентным источником тока, ток которого равен току в этой ветви, замкнутой накоротко, а внутренняя проводимость источника – входной проводимости источника.

Теорема об эквивалентном источнике тока
I = IkGвх/(Gвх + Gн)

Режимы работы реального источника ЭДС

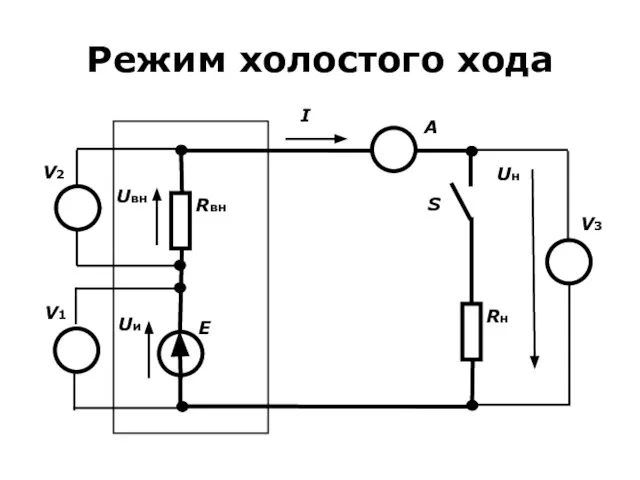
Режим холостого хода

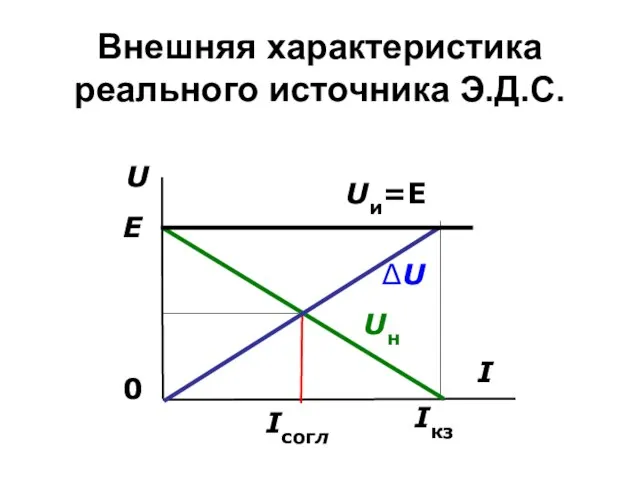
1. Режим холостого хода
Ключ S разомкнут,
Напряжение холостого хода на выходе источника равно его ЭДС (UХХ = E),
ток холостого хода равен нулю
(IХХ = 0),
сопротивление нагрузки равно бесконечности (RН = ∞),
коэффициент полезного действия (К.П.Д.) при идеальном источнике ЭДС в этом режиме стремится к единице (η = 1).

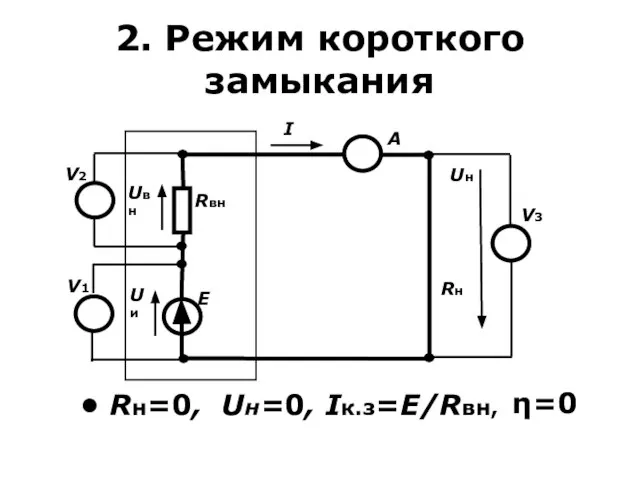
2. Режим короткого замыкания
Rн=0, Uн=0, Iк.з=E/Rвн,
η=0

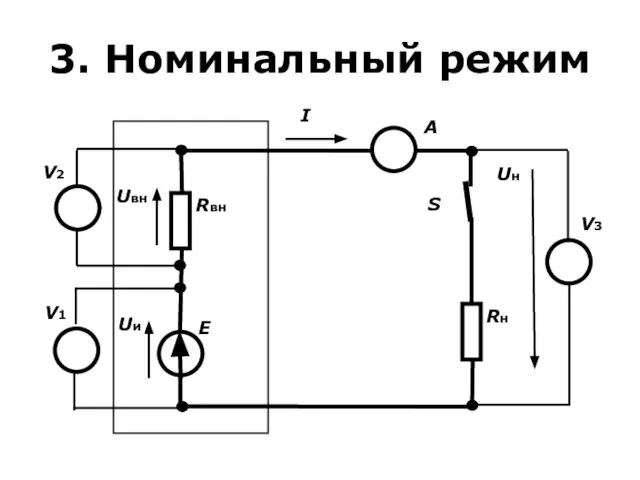
3. Номинальный режим
режим, на который рассчитывается источник, (ключ S замкнут). В этом режиме источник Е работает эффективно с точки зрения надёжности и экономичности.
< 1.
η

3. Номинальный режим

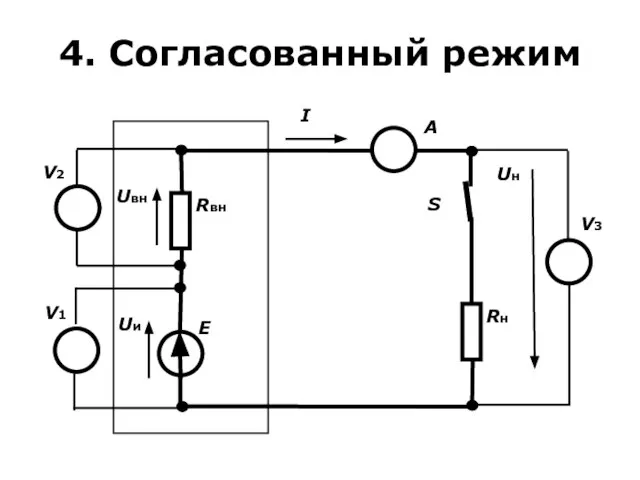
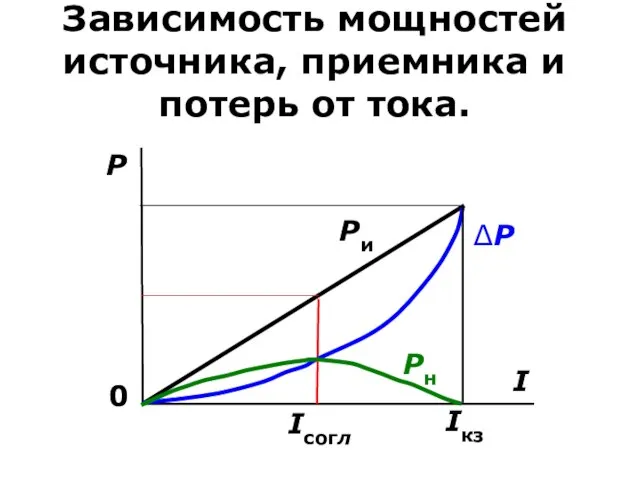
4. Согласованный режим
- это режим, при котором в нагрузку отдаётся максимальная мощность.
Мощность источника: PИ=E⋅I.
Мощность нагрузки: PН=UНАГР⋅IНАГР=I2нагр⋅ Rн.
IНАГР = , тогда
PН = ( )2 RН

4. Согласованный режим

4. Согласованный режим
Вопрос: «При какой величине RН мощность в нагрузке будет иметь максимальное значение?», т.е. нужно определить экстремум функции. Для этого возьмем
частную производную = 0

4. Согласованный режим
К.П.Д: η = Pн/Pи =
=[E2⋅Rн/(Rвн+Rн)2]·[(Rвн+Rн)/E2] =
=Rн/(Rн+Rвн) = 1/(1+Rвн/Rн) = 0,5.

4. Согласованный режим
Таким образом в согласованном режиме:
Rн = Rвн;
Pнагр = Pmax = Pист/2;
Uн = E/2;
Iн = Iк.з/2;
η = 0.5

Зависимость мощностей источника, приемника и потерь от тока.

Внешняя характеристика реального источника Э.Д.С.