Содержание
- 2. Анализ кинетических данных Кинетические параметры Характеристики каталитического процесса
- 3. Скорость реакции Экспериментальные методы определения скорости реакции Интегральные способы Дифференциальные способы Определение величины, отражающей концентрацию m
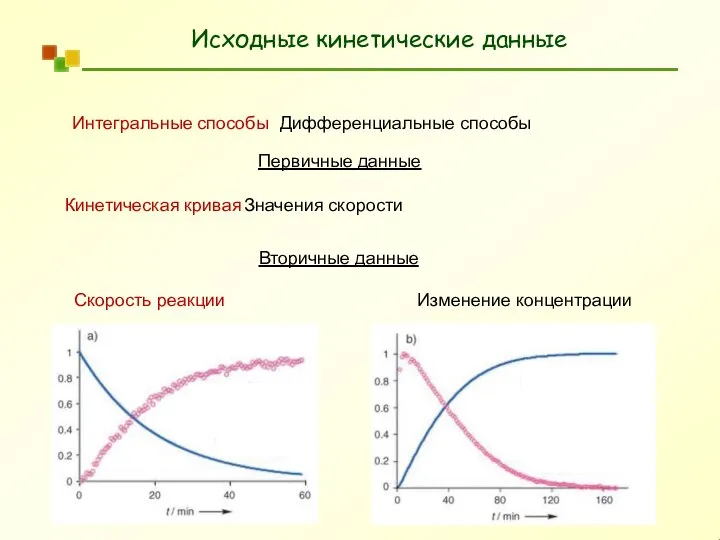
- 4. Исходные кинетические данные Интегральные способы Дифференциальные способы Первичные данные Кинетическая кривая Значения скорости Вторичные данные Скорость
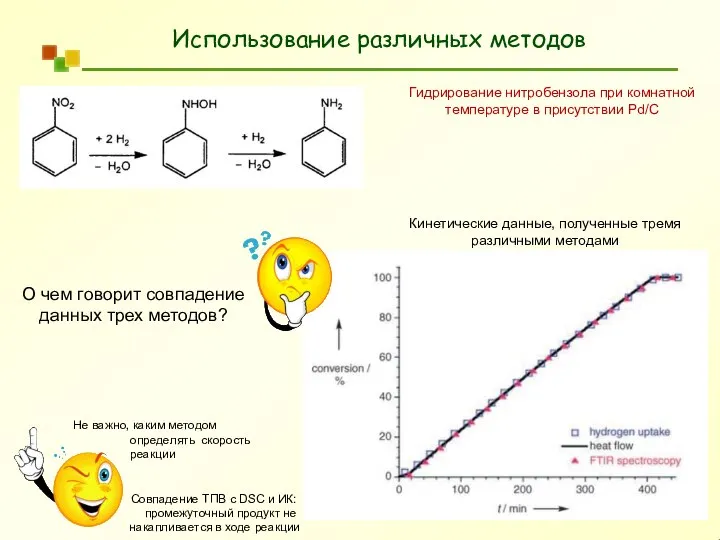
- 5. Использование различных методов Гидрирование нитробензола при комнатной температуре в присутствии Pd/C Кинетические данные, полученные тремя различными
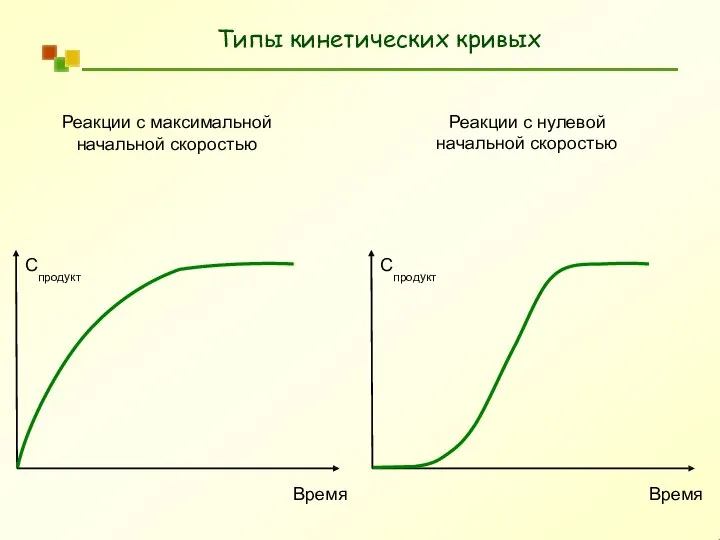
- 6. Типы кинетических кривых Время Спродукт Время Спродукт Реакции с максимальной начальной скоростью Реакции с нулевой начальной
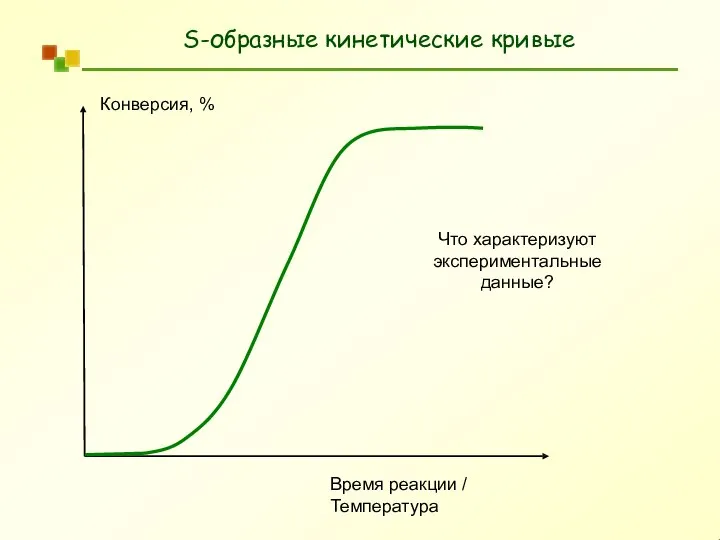
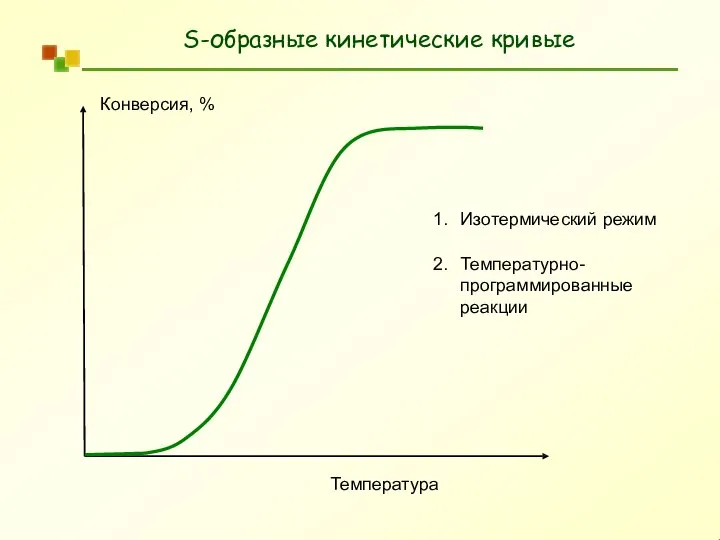
- 7. S-образные кинетические кривые Конверсия, % Время реакции / Температура Что характеризуют экспериментальные данные?
- 8. S-образные кинетические кривые Конверсия, % Температура Изотермический режим Температурно- программированные реакции
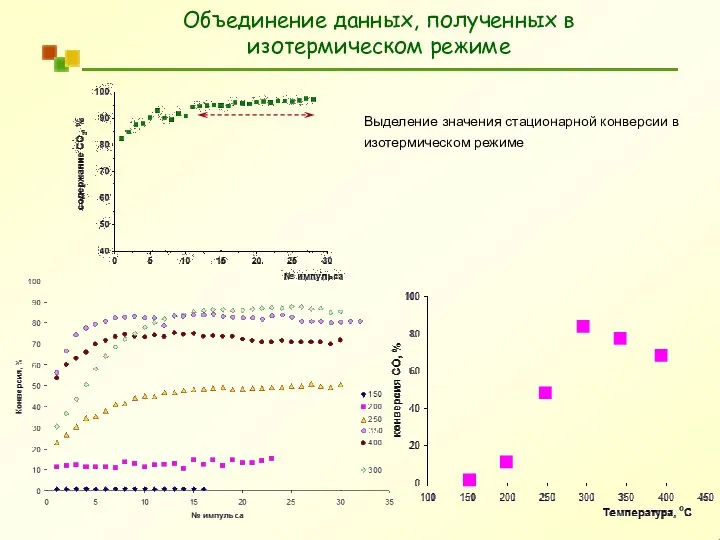
- 9. Объединение данных, полученных в изотермическом режиме Выделение значения стационарной конверсии в изотермическом режиме
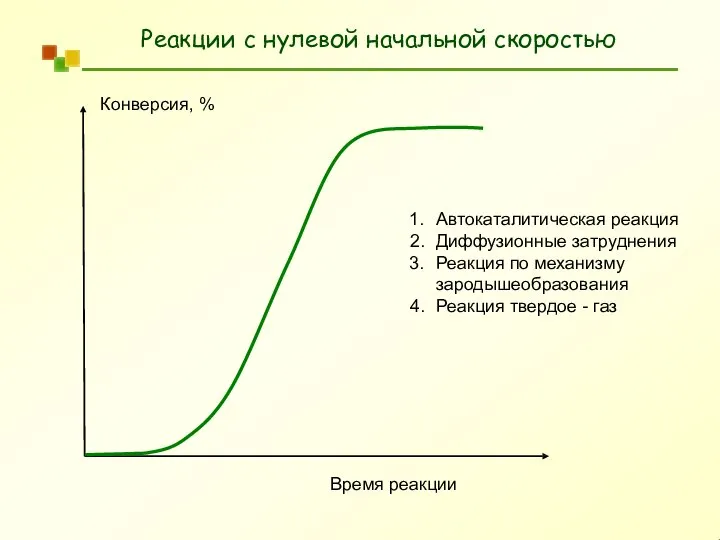
- 10. Реакции с нулевой начальной скоростью Конверсия, % Время реакции Автокаталитическая реакция Диффузионные затруднения Реакция по механизму
- 11. Скорость химической реакции A + B ? R + … r = − 1 dnA =
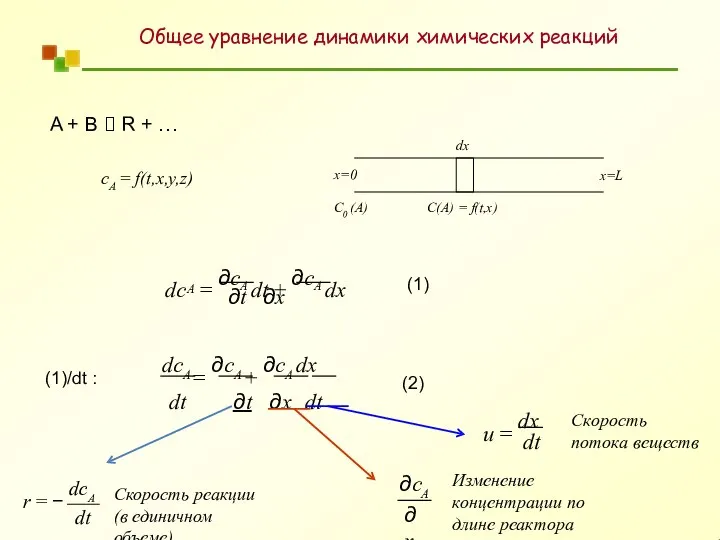
- 12. A + B ? R + … сA = f(t,x,y,z) dx x=0 C0 (A) C(A) =
- 13. u = 0 (закрытая система) dt r = − dcA = r(t ) Статическая система u
- 14. Предельные условия в реакционных системах
- 15. Статические (реакторы периодического действия) Типы химических реакторов u = 0 (закрытая система) dt r = −
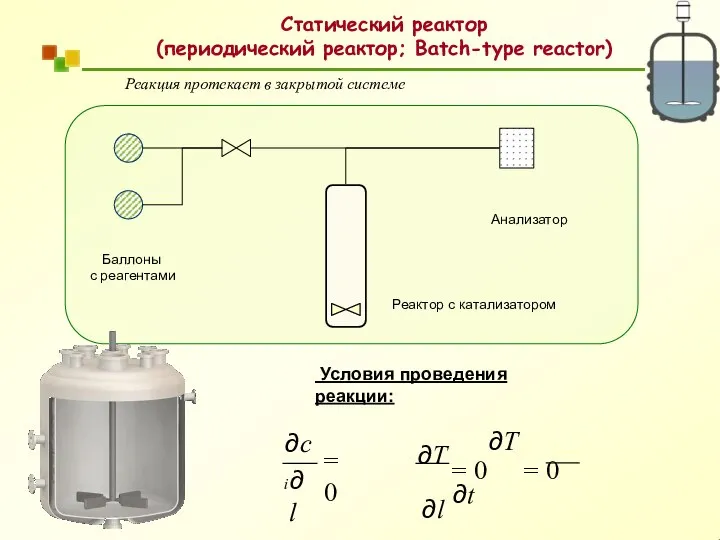
- 16. Реакция протекает в закрытой системе Условия проведения реакции: = 0 ∂l ∂ci ∂T = 0 ∂T
- 17. Статический реактор (периодический реактор; Batch-type reactor)
- 18. dt = ± dci r = ± 1 ⋅ dni V dt V = Const dt
- 19. Определение скорости реакции: Анализ состава реакционной смеси Регистрация изменения давления: реакции с изменением объема образование жидкого
- 20. Простота аппаратурного выполнения Возможность использования катализатора в любом виде (порошок, гранулы) Исследование кинетики во всем интервале
- 21. Расчет кинетических параметров реакции в статическом реакторе 2R ? P Определить порядок реакции и константу скорости
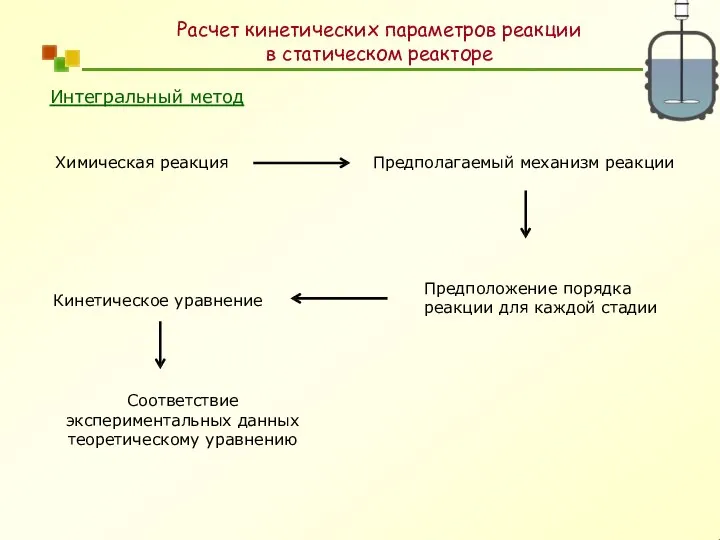
- 22. Интегральный метод Предположение порядка реакции для каждой стадии Кинетическое уравнение Соответствие экспериментальных данных теоретическому уравнению Расчет
- 23. Кинетическое уравнение для сложных реакций v(t) = k[H2 ][I2 ] H2(g) + I2 (g) ? 2HI
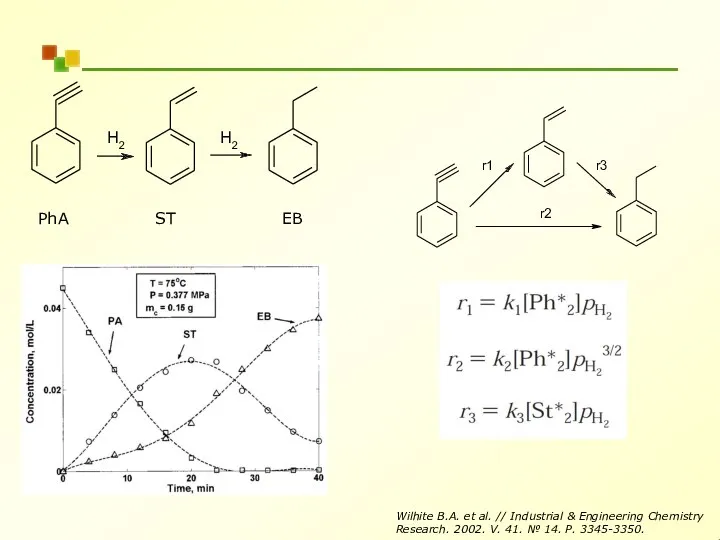
- 24. PhA ST EB H2 H2 r1 r2 r3 Wilhite B.A. et al. // Industrial & Engineering
- 25. Интегральный метод для реакций целочисленных порядков A ? B dt r = − d[ A] =
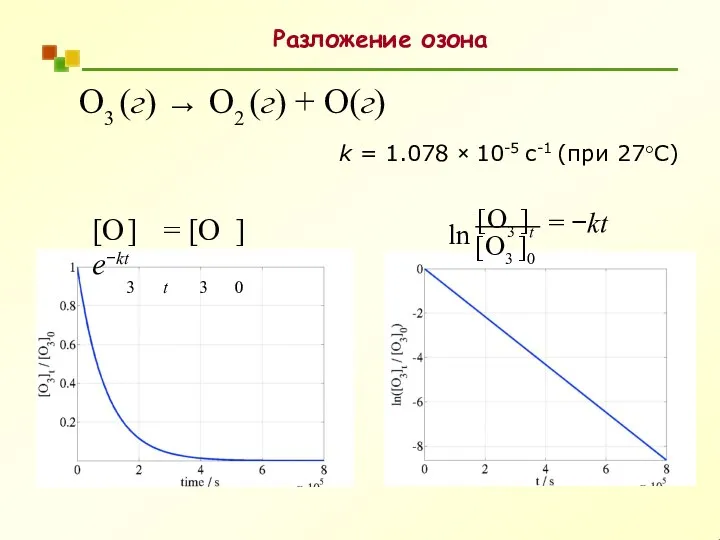
- 26. Разложение озона O3 (г) → O2 (г) + O(г) = −kt [O3 ]0 ln [O3 ]t
- 27. Реакции целочисленных порядков [ A] = [ A] e− kt t 0 = −kt [ A]0
- 28. Интегральный метод для реакций целочисленных порядков нулевой порядок первый порядок второй порядок [ A]t = [
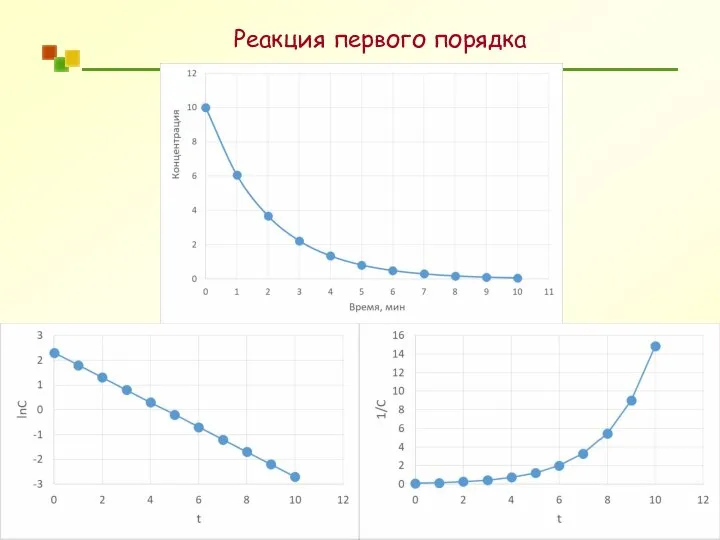
- 29. Реакция первого порядка
- 30. Реакция первого порядка = −kt [ A]0 ln [ A]t [ A] = [ A] e−
- 31. Интегральный метод: по периоду полураспада a a − x) kt = ln ( k t 1/
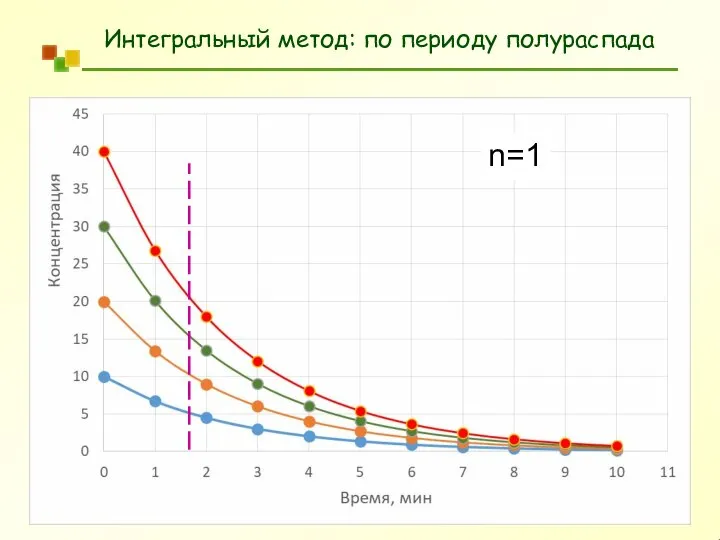
- 32. Интегральный метод: по периоду полураспада n=1
- 33. Интегральный метод: по периоду полураспада n ≠ 1 Одинаковые начальные концентрации 2n−1 −1 t1/ 2 =
- 34. Для реакции A -> продукты Определите порядок реакции, если известно: 340 140 102 = 2.9 n
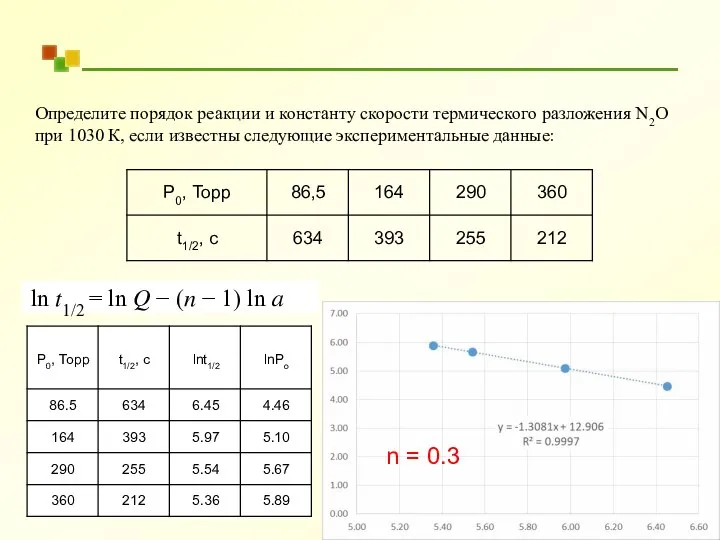
- 35. Определите порядок реакции и константу скорости термического разложения N2O при 1030 К, если известны следующие экспериментальные
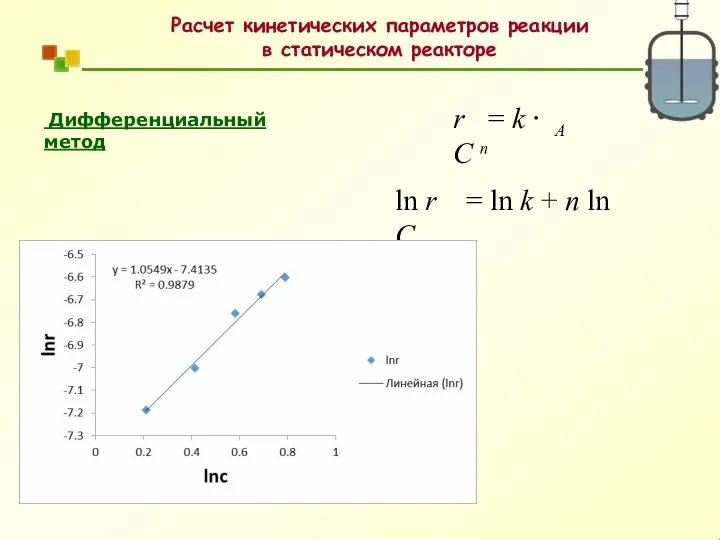
- 36. Расчет кинетических параметров реакции в статическом реакторе Дифференциальный метод A r = k ⋅ C n
- 37. Расчеты по кинетическому уравнению Для реакции первого порядка A --> продукты начальная концентрация А была 1.56
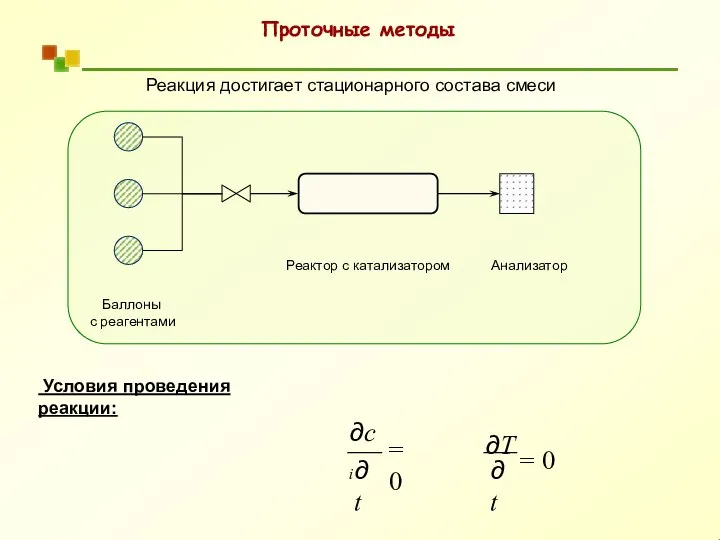
- 38. Реакция достигает стационарного состава смеси Баллоны с реагентами Реактор с катализатором Анализатор Условия проведения реакции: =
- 39. Стационарные условия Достаточное количество целевого продукта наибольшая приближенность к промышленному реактору (из лабораторных систем) Универсальный метод
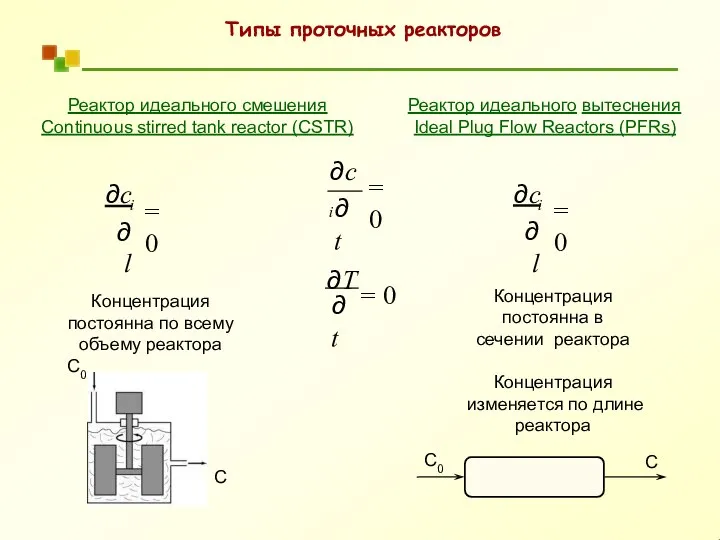
- 40. Типы проточных реакторов Реактор идеального вытеснения Ideal Plug Flow Reactors (PFRs) Реактор идеального смешения Continuous stirred
- 41. FA0 FA ∂l ∂c i = 0 dt dN FA0 − FA − rA ⋅V =
- 42. FA0 ⋅ X − rA ⋅V = 0 A CSTR r V = FA0 ⋅ X
- 43. Реактор идеального смешения Для реакции первого порядка ⇒ X A → 1 Da =τ⋅ k ↑
- 44. Реактор идеального смешения Для реакции второго порядка r V A0 A0 A CSTR k ⋅ C
- 45. Определите объем реактора идеального смешения, необходимый для превращения исходного реагента с концентрацией 0,5 моль/л с образованием
- 46. Чистый реагент А при давлении 3 атм и 30 С (120 ммоль/л) подают в реактор идеального
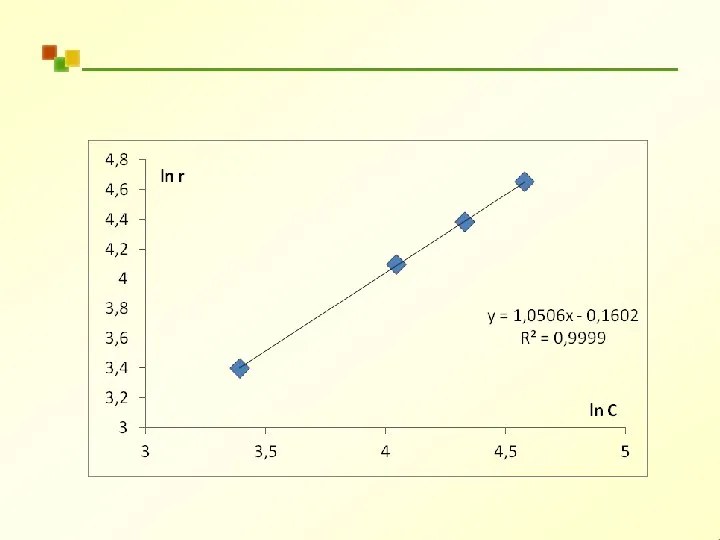
- 47. A r = k ⋅ C n ln r = ln k + n ln CA
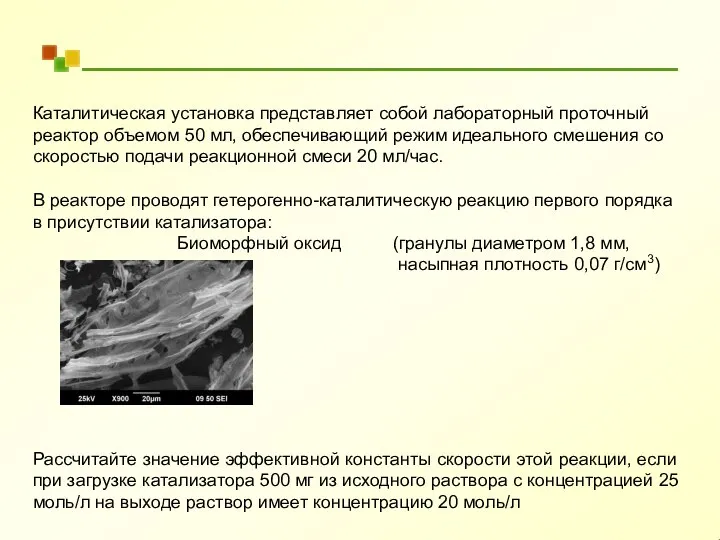
- 49. Каталитическая установка представляет собой лабораторный проточный реактор объемом 50 мл, обеспечивающий режим идеального смешения со скоростью
- 50. С0 = 25 моль/л С = 20 моль/л n = 1 Реактор: ν = 20 мл/ч
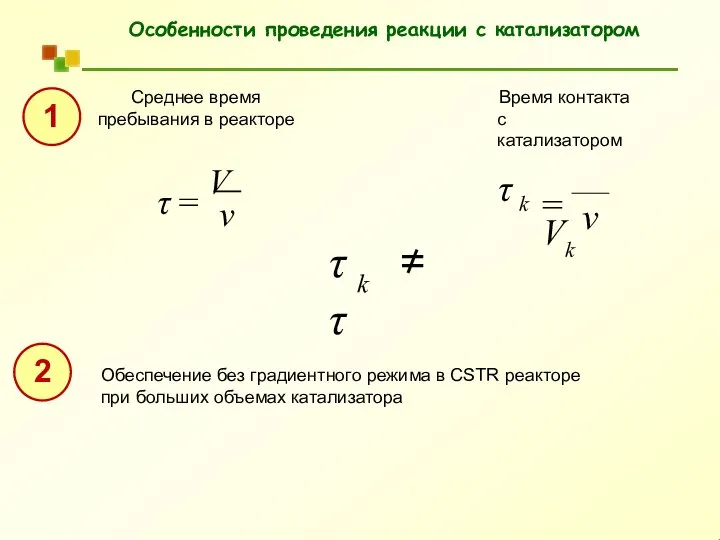
- 51. Особенности проведения реакции с катализатором Среднее время пребывания в реакторе v τ = V Время контакта
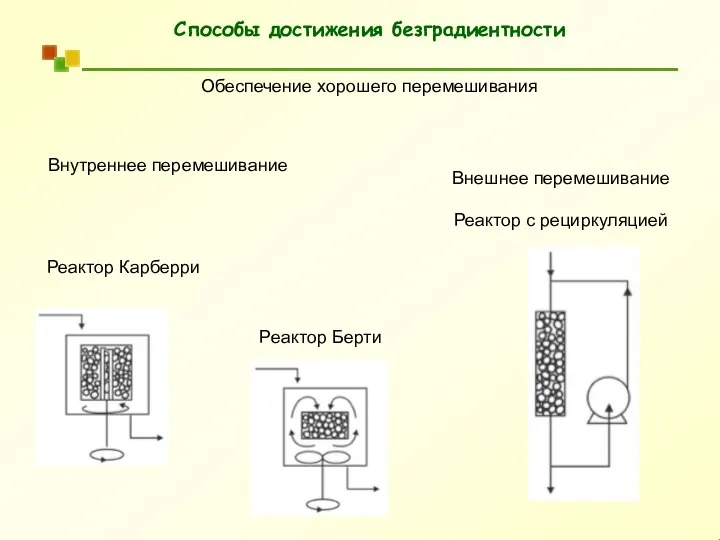
- 52. Способы достижения безградиентности Обеспечение хорошего перемешивания Внутреннее перемешивание Внешнее перемешивание Реактор с рециркуляцией Реактор Карберри Реактор
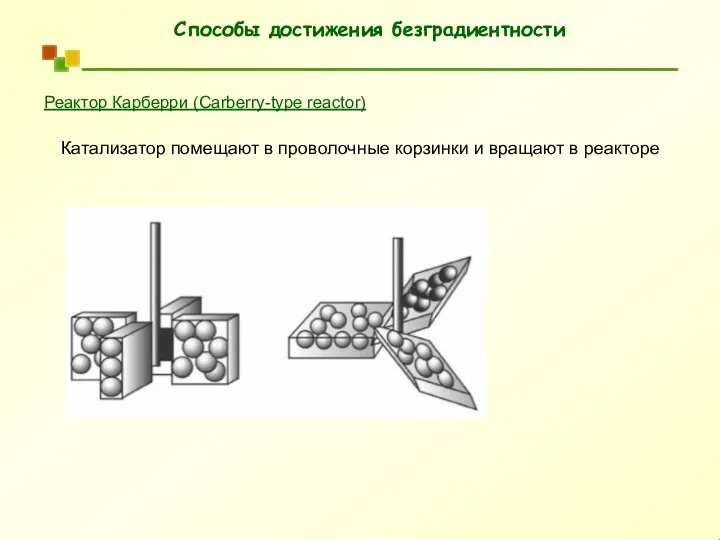
- 53. Реактор Карберри (Carberry-type reactor) Катализатор помещают в проволочные корзинки и вращают в реакторе Способы достижения безградиентности
- 55. Скачать презентацию











![Кинетическое уравнение для сложных реакций v(t) = k[H2 ][I2 ] H2(g) +](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1026836/slide-22.jpg)

![Реакции целочисленных порядков [ A] = [ A] e− kt t 0](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1026836/slide-26.jpg)

![Реакция первого порядка = −kt [ A]0 ln [ A]t [ A]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1026836/slide-29.jpg)













 Масштаб аэрофотоснимков
Масштаб аэрофотоснимков Устройство и принцип работы дизельного двигателя
Устройство и принцип работы дизельного двигателя Плотность. Плотность мрамора
Плотность. Плотность мрамора Клепаные и сварные соединения
Клепаные и сварные соединения Квантовая физика. Фотоэффект
Квантовая физика. Фотоэффект Русские изобретения, которыми пользуется весь мир
Русские изобретения, которыми пользуется весь мир Деформация Сила упругости, закон Гука (Тема 1, Тема 2)
Деформация Сила упругости, закон Гука (Тема 1, Тема 2) Ветровой электрогенератор challenergy
Ветровой электрогенератор challenergy I-D диаграмма влажного воздуха
I-D диаграмма влажного воздуха Рычаг первого рода
Рычаг первого рода Сопротивление материалов
Сопротивление материалов Тепловое расширение
Тепловое расширение А.В.Перышкин Физика, 8 класс. Решение задач
А.В.Перышкин Физика, 8 класс. Решение задач Теория и практика формообразования заготовок
Теория и практика формообразования заготовок Проверь себя!!!
Проверь себя!!! Первый пароход 4/2 класс
Первый пароход 4/2 класс Законы сохранения в механике. Лекция № 5
Законы сохранения в механике. Лекция № 5 Механика деформируемого твердого тела
Механика деформируемого твердого тела Давление твердых тел
Давление твердых тел Светофор. Внеклассное мероприятие по физике
Светофор. Внеклассное мероприятие по физике Понятие индукции
Понятие индукции Ядерный реактор
Ядерный реактор Электростатика
Электростатика Презентация на тему Давление света
Презентация на тему Давление света  Задачи на соединение проводников
Задачи на соединение проводников Презентация по физике "Скорость" -
Презентация по физике "Скорость" -  Относительность движения
Относительность движения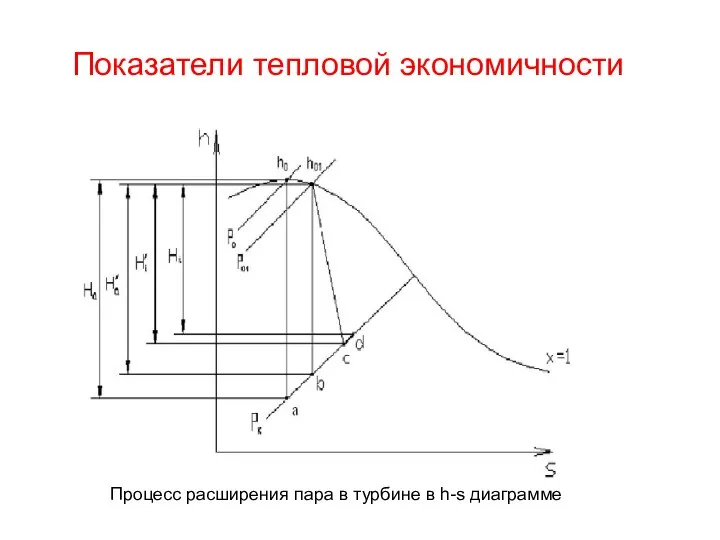 Показатели тепловой экономичности
Показатели тепловой экономичности