Слайд 25. Движение в неинерциальных системах отсчёта.
Рассмотренные выше законы динамики справедливы лишь в

инерциальных системах отсчёта, телами отсчёта которых являются свободные тела. Однако, абсолютно свободных тел в природе не существует. Это значит, что инерциальных систем отсчёта в строгом смысле в природе не существует.
Слайд 3Мера неинерциальности.
Все реальные системы отсчёта движутся с тем или иным ускорением. Это

ускорение – собственное ускорение систем отсчёта – и является мерой неинерциальности системы. Чем больше собственное ускорение системы отсчёта, тем в большей степени она неинерциальна.
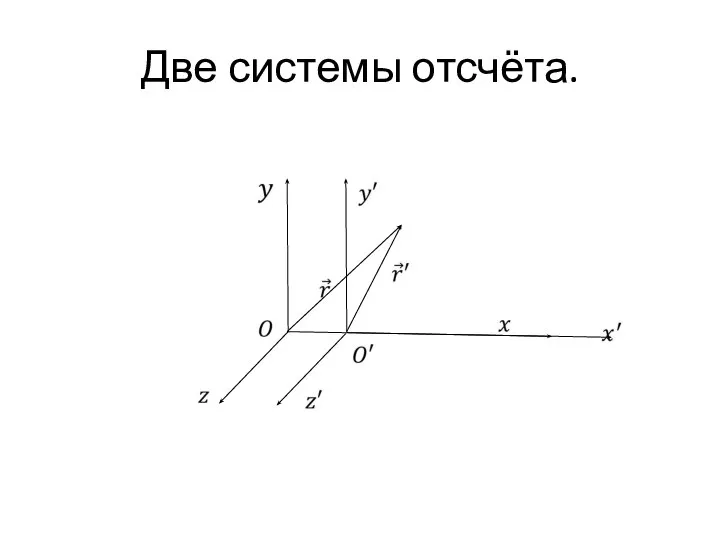
Слайд 6Преобразование радиусов-векторов.

Слайд 9Формулы преобразования скоростей.

Слайд 10Равномерное движение подвижной системы.

Слайд 11Ускоренное движение подвижной системы.

Слайд 12Второй закон Ньютона для неинерциальной системы отсчёта.

Слайд 14Формулировка второго закон Ньютона для неинерциальных систем отсчёта.
Это утверждение и носит название

второго закона Ньютона для неинерциальных систем отсчёта. Оно гласит, что второй закон Ньютона справедлив и для неинерциальных систем отсчёта, только к реально действующим силам необходимо добавить т.н. силы инерции.
Слайд 15Центробежная сила и сила Кориолиса

Слайд 166. Движение твёрдого тела.
6.1. Кинематика твёрдого тела.
Определение. Твёрдым телом называется система материальных

точек, расстояние между любыми двумя из которых остаётся неизменным при движении системы.
Существует два принципиально различных вида движения твёрдого тела: поступательное и вращательное.
Слайд 17Поступательное движение т.т.
Определение. Поступательным движением т.т. называется такое движение, при котором прямая,

проходящая через любые две его точки, остаётся параллельной самой себе.
При поступательном движении т.т. все его точки движутся совершенно одинаково, по параллельным траекториям с одинаковыми скоростями. Поэтому всё движение можно охарактеризовать одной скоростью.
Слайд 18Демонстрация.
Progr D: Progr E: Progr F: Progr G:

Слайд 19Вращательное движение т.т.
Определение. Вращательным движением т.т. называется такое движение, при котором траекториями

движения его точек являются окружности.
Т.к. расстояние между точками т.т. не могут меняться, центры окружностей, по которым движутся точки т.т. должны быть расположены на одной прямой.
Слайд 20Ось вращения т.т.
Определение. Прямая, на которой расположены центры окружностей, по которым движутся

точки т.т. при вращении, называется осью вращения т.т.
Слайд 24Связь угловой скорости вращения т.т. с частотой.

Слайд 25Вектор угловой скорости.
Угловая скорость т.т. считается векторной величиной, направленной по оси вращения

т.т. так, что с конца вектора угловой скорости вращение выполняется против часовой стрелки. По-другому направление угловой скорости можно определить с помощью правила правого винта или правила буравчика: если винт, расположенный по оси вращения т.т., вращать, как вращается т.т., то движение винта вследствие резьбы покажет направление угловой скорости.
Слайд 26Связь угловой и линейной скорости.

Слайд 27Векторная связь угловой и линейной скорости.

Слайд 32Следствия из определения углового ускорения.

































 Соединение обмоток генератора треугольником
Соединение обмоток генератора треугольником Мимеография
Мимеография Велосипед: из чего состоит и его характеристики
Велосипед: из чего состоит и его характеристики Презентация на тему Теория фотоэффекта
Презентация на тему Теория фотоэффекта  Жидкие кристаллы
Жидкие кристаллы Телескопы
Телескопы Излучение электромагнитного поля. Антенны
Излучение электромагнитного поля. Антенны Чистые источники энергии. Выполнила: учитель физики ГБОУ ЦО «Школа здоровья» №628 Лисицкая Елена Владимировна
Чистые источники энергии. Выполнила: учитель физики ГБОУ ЦО «Школа здоровья» №628 Лисицкая Елена Владимировна Тест по теме Архимедова сила. Плавание тел
Тест по теме Архимедова сила. Плавание тел Метрология ионизирующих излучений. (Лекция 3)
Метрология ионизирующих излучений. (Лекция 3) Телефон без электричества. Физика
Телефон без электричества. Физика Механика. Законы сохранения в механике
Механика. Законы сохранения в механике Презентация на тему Простые механизмы
Презентация на тему Простые механизмы  Решение задач по теме Электрический ток
Решение задач по теме Электрический ток Метод рефрактометрии и ИК-спектроскопии
Метод рефрактометрии и ИК-спектроскопии Урок 7
Урок 7 Величайшие открытия физики
Величайшие открытия физики Тепловые двигатели
Тепловые двигатели Расчет давления и атомных напряжений в МД
Расчет давления и атомных напряжений в МД Сообщающиеся сосуды. 7 класс
Сообщающиеся сосуды. 7 класс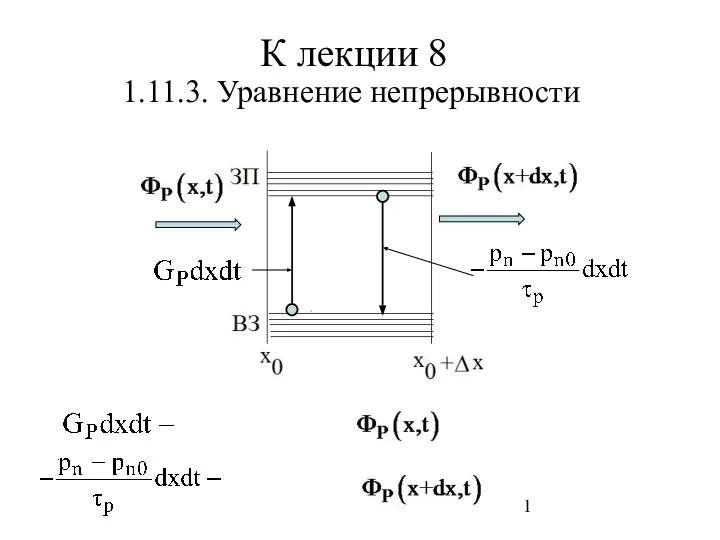 Уравнение непрерывности
Уравнение непрерывности Термодинамика
Термодинамика Коллективные спасательные средства. Тема 2.3
Коллективные спасательные средства. Тема 2.3 Лекция 7. Расчет статически неопределимых систем методом сил
Лекция 7. Расчет статически неопределимых систем методом сил Практическое занятие. Расчет тока КЗ
Практическое занятие. Расчет тока КЗ Последовательное и параллельное соединения проводников
Последовательное и параллельное соединения проводников Электрические силы
Электрические силы Движение. Тело отсчёта
Движение. Тело отсчёта