Содержание
- 2. Учебные цели: Кафедра №2, ВАС Изучить процесс формирования шума (ошибок) квантования и свойства шума квантования. Дать
- 3. Учебные вопросы: Кафедра №2, ВАС Способы квантования чисел. Шум аналого-цифрового преобразования. Собственный шум цифровой цепи. Эффекты
- 4. Литература для самостоятельной работы обучаемых: Кафедра №2, ВАС 1. Цифровая обработка сигналов. Краткий курс/ Д. А.
- 5. Первый учебный вопрос Кафедра №2, ВАС Способы квантования чисел
- 6. Первый учебный вопрос Кафедра №2, ВАС 1. Источники шума (ошибок) квантования; допущения о свойствах шума квантования
- 7. Первый учебный вопрос Кафедра №2, ВАС 1. Источники шума (ошибок) квантования; допущения о свойствах шума квантования
- 8. Первый учебный вопрос Кафедра №2, ВАС 1. Источники шума (ошибок) квантования; допущения о свойствах шума квантования
- 9. Первый учебный вопрос Кафедра №2, ВАС 1. Источники шума (ошибок) квантования; допущения о свойствах шума квантования
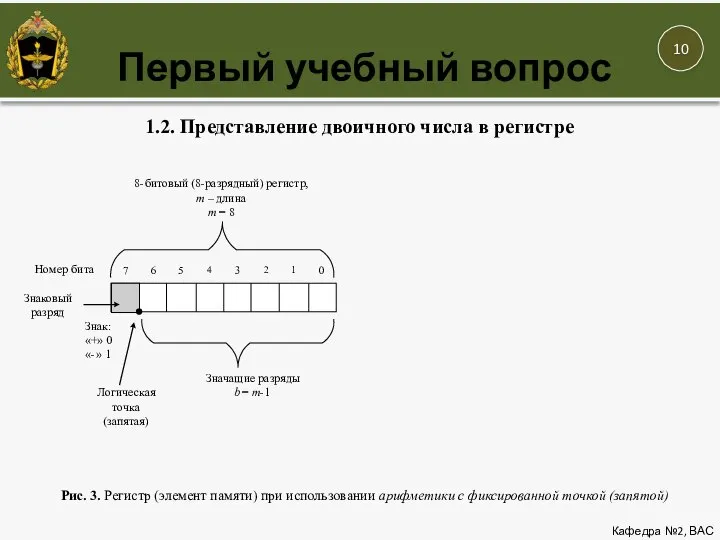
- 10. Первый учебный вопрос Кафедра №2, ВАС
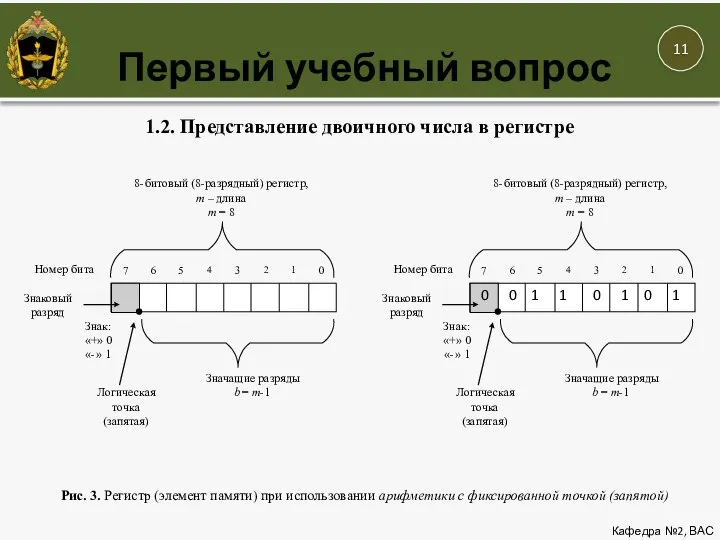
- 11. Первый учебный вопрос Кафедра №2, ВАС
- 12. Первый учебный вопрос Кафедра №2, ВАС Квантование выполняется двумя способами: 1. Усечение k-разрядного числа до b
- 13. Первый учебный вопрос Кафедра №2, ВАС Квантование выполняется двумя способами: 1. Усечение k-разрядного числа до b
- 14. Первый учебный вопрос Кафедра №2, ВАС Прямой код используется при выполнении умножения
- 15. Первый учебный вопрос Кафедра №2, ВАС Прямой код используется при выполнении умножения Обратный код
- 16. Первый учебный вопрос Кафедра №2, ВАС Прямой код используется при выполнении умножения Обратный код Дополнительный код
- 17. Первый учебный вопрос Кафедра №2, ВАС x(t) – аналоговый сигнал, подвергающийся дискретизации, x͂(n)– дискретный сигнал с
- 18. Второй учебный вопрос Кафедра №2, ВАС Шум аналого-цифрового преобразования
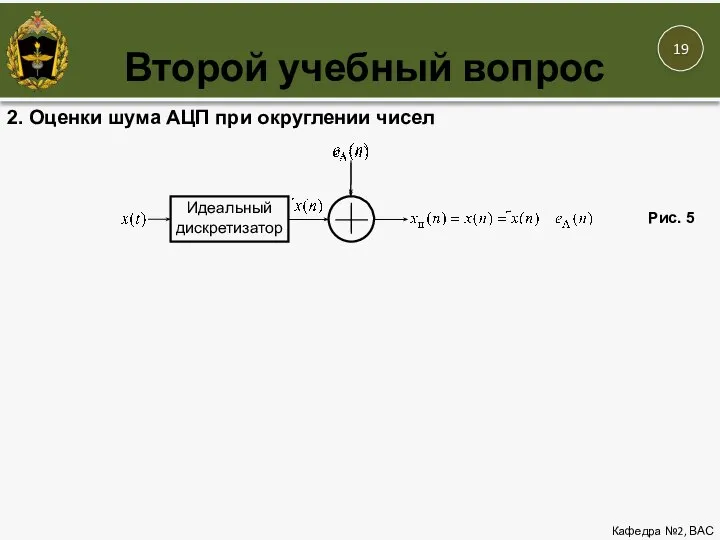
- 19. Второй учебный вопрос Кафедра №2, ВАС Идеальный дискретизатор 2. Оценки шума АЦП при округлении чисел Рис.
- 20. Второй учебный вопрос Кафедра №2, ВАС Идеальный дискретизатор 2. Оценки шума АЦП при округлении чисел Рис.
- 21. Второй учебный вопрос Кафедра №2, ВАС Идеальный дискретизатор 2. Оценки шума АЦП при округлении чисел Рис.
- 22. Второй учебный вопрос Кафедра №2, ВАС Идеальный дискретизатор 2. Оценки шума АЦП при округлении чисел Рис.
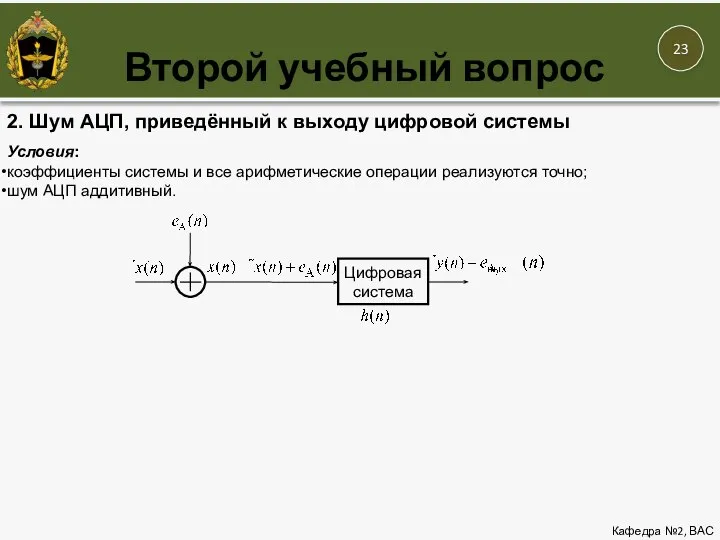
- 23. Второй учебный вопрос Кафедра №2, ВАС 2. Шум АЦП, приведённый к выходу цифровой системы Условия: коэффициенты
- 24. Второй учебный вопрос Кафедра №2, ВАС 2. Шум АЦП, приведённый к выходу цифровой системы Условия: коэффициенты
- 25. Второй учебный вопрос Кафедра №2, ВАС
- 26. Третий учебный вопрос Кафедра №2, ВАС Собственный шум цифровой системы
- 27. Третий учебный вопрос Кафедра №2, ВАС Определение: Собственный шум цифровой системы — это выходной шум квантования,
- 28. Третий учебный вопрос Кафедра №2, ВАС Определение: Собственный шум цифровой системы — это выходной шум квантования,
- 29. Третий учебный вопрос Кафедра №2, ВАС 1. Собственный шум умножителя Рис. 7. Линейная модель умножителя с
- 30. Третий учебный вопрос Кафедра №2, ВАС 3.2. Полный собственный шум цепи Составляющие полного собственного шума —
- 31. Третий учебный вопрос Кафедра №2, ВАС Полный собственный шум цепи Математическое ожидание Дисперсия Абсолютная граница Полный
- 32. Четвертый учебный вопрос Кафедра №2, ВАС Эффекты квантования в цифровых цепях
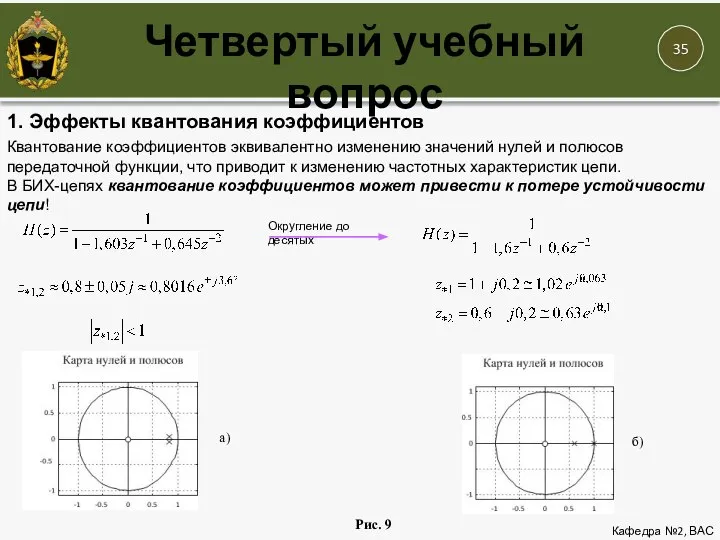
- 33. Кафедра №2, ВАС Четвертый учебный вопрос Квантование коэффициентов эквивалентно изменению значений нулей и полюсов передаточной функции,
- 34. Кафедра №2, ВАС Четвертый учебный вопрос Квантование коэффициентов эквивалентно изменению значений нулей и полюсов передаточной функции,
- 35. Кафедра №2, ВАС Четвертый учебный вопрос Квантование коэффициентов эквивалентно изменению значений нулей и полюсов передаточной функции,
- 36. Кафедра №2, ВАС Четвертый учебный вопрос 2. Понятие о предельных циклах Виды предельных циклов: предельные циклы
- 37. Четвертый учебный вопрос Кафедра №2, ВАС 3. Переполнение в сумматорах и коэффициенты масштабирования Определение: Переполнением называют
- 38. Четвертый учебный вопрос Кафедра №2, ВАС 3. Переполнение в сумматорах и коэффициенты масштабирования Определение: Переполнением называют
- 39. Четвертый учебный вопрос Кафедра №2, ВАС 3. Переполнение в сумматорах и коэффициенты масштабирования Определение: Переполнением называют
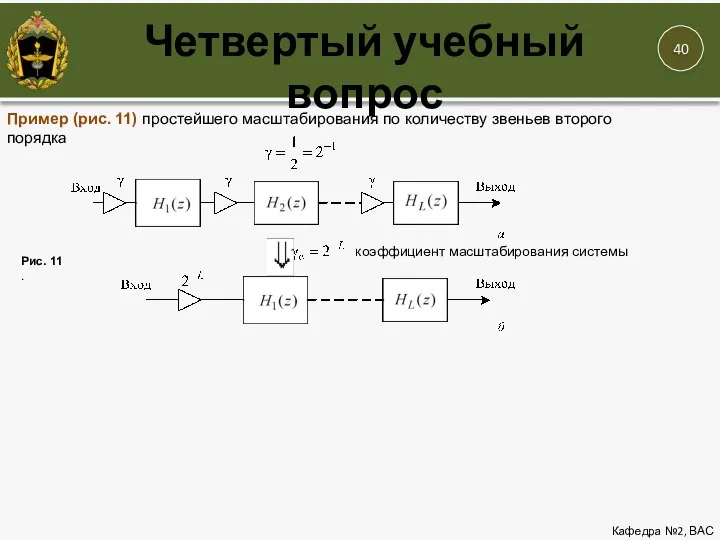
- 40. Четвертый учебный вопрос Кафедра №2, ВАС Пример (рис. 11) простейшего масштабирования по количеству звеньев второго порядка
- 41. Заключение Кафедра №2, ВАС В цифровых системах проблема точности представления параметров системы (коэффициентов передаточных функций и
- 43. Скачать презентацию


































 Амплитудная цилиндрическая дифракционная линза. Расчет, изготовление с помощью фотолитографии и жидкостного травления
Амплитудная цилиндрическая дифракционная линза. Расчет, изготовление с помощью фотолитографии и жидкостного травления Давление твердых тел
Давление твердых тел Атомно-абсорбционная спектроскопия
Атомно-абсорбционная спектроскопия Цилиндрические прямозубые передачи
Цилиндрические прямозубые передачи Звуки природы и звуки космоса. Что их объединяет
Звуки природы и звуки космоса. Что их объединяет Закон Джоуля-Ленца
Закон Джоуля-Ленца etalon_otredaktirovana_LEKTsIYa_8_ioniziruyuschee_ETALON
etalon_otredaktirovana_LEKTsIYa_8_ioniziruyuschee_ETALON Изменение агрегатного состояния вещества
Изменение агрегатного состояния вещества Последовательное соединение проводников
Последовательное соединение проводников Физические величины. Измерение физических величин. Точность и погрешность измерений
Физические величины. Измерение физических величин. Точность и погрешность измерений Электрический ток в вакууме
Электрический ток в вакууме Разность потенциалов
Разность потенциалов Задачи
Задачи Руководство для выполнения графических работ. Начертательная геометрия
Руководство для выполнения графических работ. Начертательная геометрия Масса, плотность, объём. (Решение задач с использованием эксперимента)
Масса, плотность, объём. (Решение задач с использованием эксперимента) Кинематика
Кинематика Оптичні ілюзії
Оптичні ілюзії Автоматическое управление. Типовая упрощенная структура САУ
Автоматическое управление. Типовая упрощенная структура САУ Исследование аэродинамических характеристик модели крыла
Исследование аэродинамических характеристик модели крыла Способы увеличения и уменьшения давления
Способы увеличения и уменьшения давления Автопогрузчик H14-80 Evo серия 39X
Автопогрузчик H14-80 Evo серия 39X Тепловые электрические станции
Тепловые электрические станции Строение твердых тел, жидкостей и газов
Строение твердых тел, жидкостей и газов Физика в картинках
Физика в картинках Физическая викторина
Физическая викторина Проектирование содержания образования (СО). Модуль
Проектирование содержания образования (СО). Модуль Основные понятия и терминология. Погрешность измерений. Классификация
Основные понятия и терминология. Погрешность измерений. Классификация Плазма и её использование
Плазма и её использование