Содержание
- 2. метод непосредственной оценки – это метод, при котором значение величины определяют непосредственно по показывающему средству измерений.
- 3. метод сравнения с мерой – это метод измерений, в котором измеряемую величину сравнивают с величиной, воспроизводимой
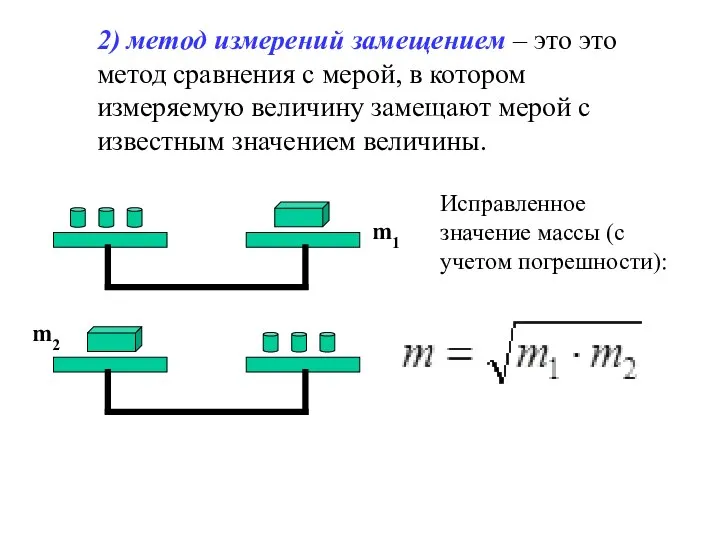
- 4. 2) метод измерений замещением – это это метод сравнения с мерой, в котором измеряемую величину замещают
- 5. 3) дифференциальный метод (разностный метод) – это метод измерений, при котором измеряемая величина сравнивается с однородной
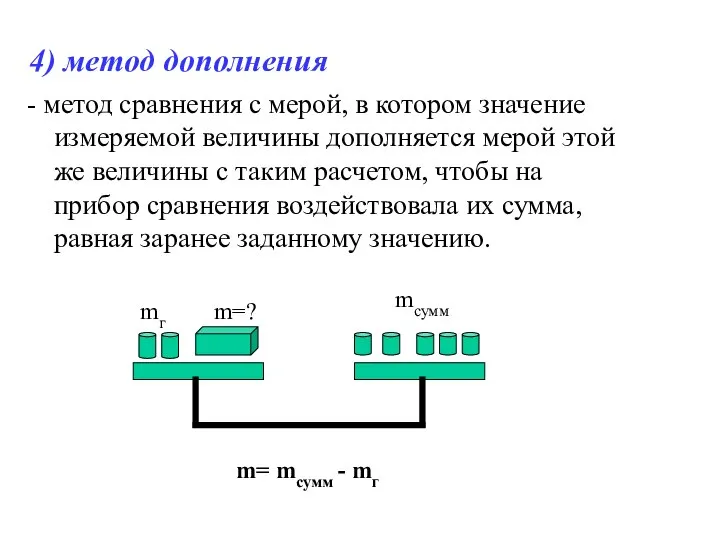
- 6. 4) метод дополнения - метод сравнения с мерой, в котором значение измеряемой величины дополняется мерой этой
- 7. Контактный метод - метод измерений, основанный на том, что чувствительный элемент прибора приводится в контакт с
- 8. Основные преимущества СИ: десятичная система образования кратных и дольных единиц, соответствующая десятичной системе нашего числового счета.
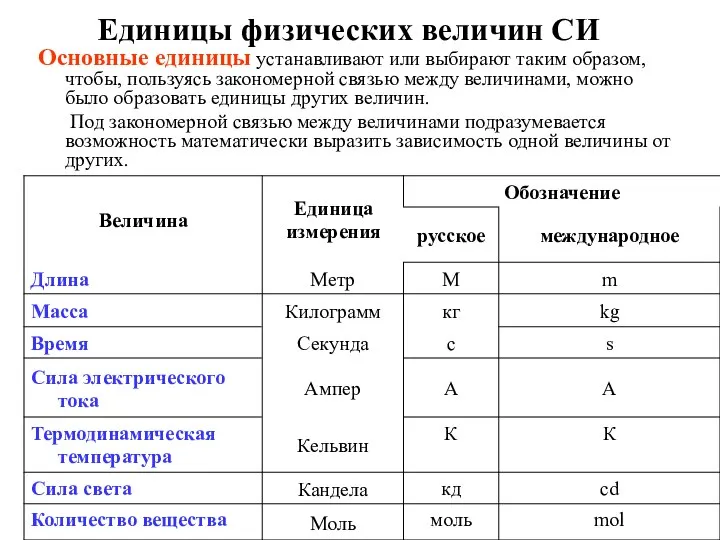
- 9. Единицы физических величин СИ Основные единицы устанавливают или выбирают таким образом, чтобы, пользуясь закономерной связью между
- 11. - величины, входящие в систему величин и определяемые через основные величины этой системы. Они образуются на
- 14. Дополнительные единицы СИ для образования единиц угловой скорости, углового ускорения и др. Радиан — угол между
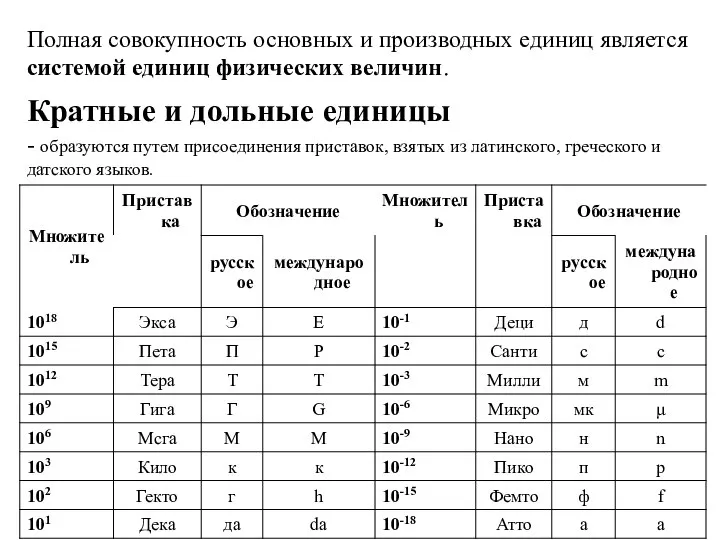
- 15. Полная совокупность основных и производных единиц является системой единиц физических величин. Кратные и дольные единицы -
- 16. Особенности метода построения системы единиц величин: 1. Размеры производных единиц зависят от размеров основных единиц. S=a*b
- 17. §3. ПОГРЕШНОСТИ ИЗМЕРЕНИЙ Погрешность измерения – разность между измеренным значением величины и опорным значением величины. Если
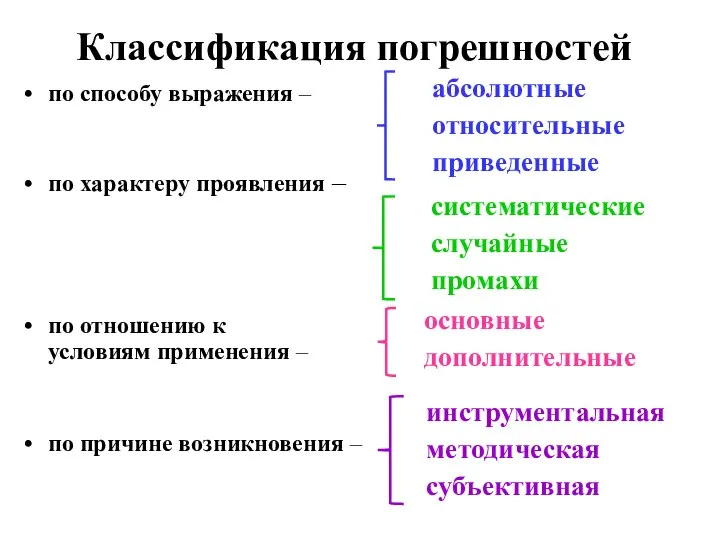
- 18. Классификация погрешностей по способу выражения – по характеру проявления – по отношению к условиям применения –
- 19. Абсолютную погрешность определяют как разность Δ = x – xд, т.е. это погрешность измерения, выраженная в
- 20. Относительная погрешность является наиболее информативной, так как дает возможность объективно сопоставлять результаты и оценивать качество измерений
- 21. Исключение указанного недостатка возможно при нормировании приведенной погрешности измерения. Приведенной γ называется относительная погрешность, выраженная в
- 22. Инструментальная погрешность - это составляющая погрешности измерения, обусловленная погрешностью применяемого средства измерений. 2. Методическая погрешность обусловлена
- 23. Случайная погрешность это составляющая погрешности измерения, изменяющаяся случайным образом (по знаку и значению) при повторных измерениях,
- 24. Случайные погрешности измерений Если полностью исключить систематические погрешности, то случайные погрешности: равные по абсолютной величине положительные
- 25. Систематические погрешности это составляющая погрешности измерения, остающаяся постоянной или же закономерно изменяющаяся при повторных измерениях одной
- 26. ГРУБЫЕ ПОГРЕШНОСТИ (ПРОМАХИ) погрешность, возникшая вследствие недосмотра оператора или неисправности прибора (например, если оператор неправильно прочёл
- 27. Систематические погрешности и способы их обнаружения и устранения Инструментальные погрешности возрастают, как правило, при увеличении срока
- 28. 2.2 Практические погрешности — это погрешности установки прибора и погрешность оператора. Погрешности установки прибора — отклонения
- 29. 3. Погрешности внешних влияний Используют следующие пути учета и исключения систематических погрешностей от внешних воздействий: 1.
- 30. Суммирование погрешностей измерений. это определение расчетным путем оценки результирующей погрешности по известным оценкам ее составляющих. На
- 31. Примеры: Q=a + b + c + ... + n: Если суммируемых составляющих более 5, то
- 32. Кривая нормального распределения случайной величины р(х) – дифференциальная функция распределения случайной величины; σ – среднее квадратическое
- 34. Скачать презентацию


























 Машина Голдберга
Машина Голдберга Автономные инверторы
Автономные инверторы Расчет измерительных преобразователей
Расчет измерительных преобразователей Насыщенный пар. Кипение. Влажность воздуха. Уроки физики в 10 классе
Насыщенный пар. Кипение. Влажность воздуха. Уроки физики в 10 классе Технологии беспроводной передачи энергии методом электромагнитной индукции
Технологии беспроводной передачи энергии методом электромагнитной индукции Зубчатые колеса
Зубчатые колеса Силы в природе
Силы в природе Деформація
Деформація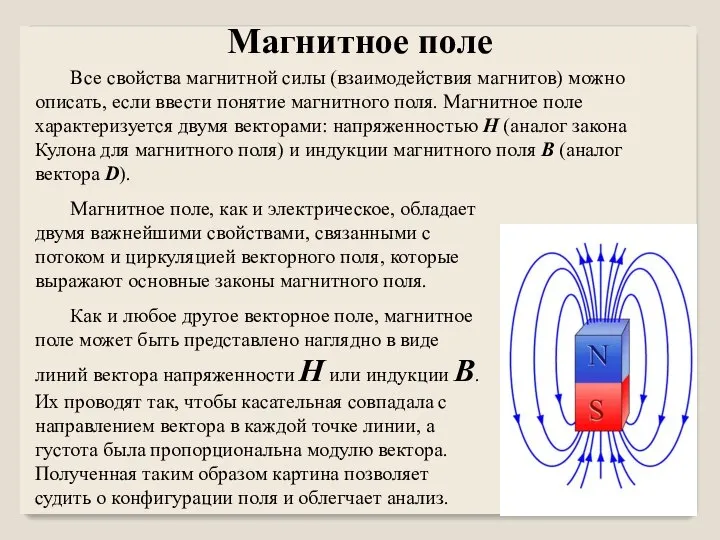 Магнитное поле
Магнитное поле Проектирование компрессорных установок горных предприятий. Занятие 7
Проектирование компрессорных установок горных предприятий. Занятие 7 Пространство, время, движение (Тема 1)
Пространство, время, движение (Тема 1) Энергия топлива. Удельная теплота сгорания топлива
Энергия топлива. Удельная теплота сгорания топлива Еволюція фізичної картини світу. Фізика і науково-технічний прогрес. Урок 98
Еволюція фізичної картини світу. Фізика і науково-технічний прогрес. Урок 98 Физическая природа изображений
Физическая природа изображений Физические и химические явления. 8 класс
Физические и химические явления. 8 класс Различные свойства вещества
Различные свойства вещества Формула бинома Ньютона. Свойства биноминальных коэффициентов
Формула бинома Ньютона. Свойства биноминальных коэффициентов Защита проекта. Мойка и увлажнитель воздуха
Защита проекта. Мойка и увлажнитель воздуха Применение физических законов при решении задач по астрофизике
Применение физических законов при решении задач по астрофизике Теория парамагнетизма
Теория парамагнетизма Электромагнитные колебания и волны
Электромагнитные колебания и волны Шагающая вода. Исследовательский проект
Шагающая вода. Исследовательский проект Презентация на тему Ультразвук
Презентация на тему Ультразвук  РЛС воздушного наблюдения антенно-волноводного тракта
РЛС воздушного наблюдения антенно-волноводного тракта Электрические цепи и их элементы
Электрические цепи и их элементы Оценка параметров движения при зондировании последовательностью оптических импульсов
Оценка параметров движения при зондировании последовательностью оптических импульсов Сказка про радио
Сказка про радио Методы получения вакуума
Методы получения вакуума