Содержание
- 2. Электрический заряд 2. Существует наименьший электрический заряд (элементарный) 1. Существует два типа электрических зарядов + -
- 3. Заряды элементарных частиц Протоны имеют положительный заряд ер = +1,6 •10-19 Кл Электроны имеют отрицательный заряд
- 4. Макроскопические тела в нормальных условиях в среднем электро-нейтральны. Но! Можно отделить часть отрицательного заряда (часть электронов)
- 5. Закон сохранения электрического заряда. В замкнутой системе алгебраическая сумма электрических зарядов всех частиц остается неизменной. Закон
- 6. Электрические заряды – демонстрационные опыты «Открытое образование», курс «Физика в опытах», часть 3 Электрические и магнитные
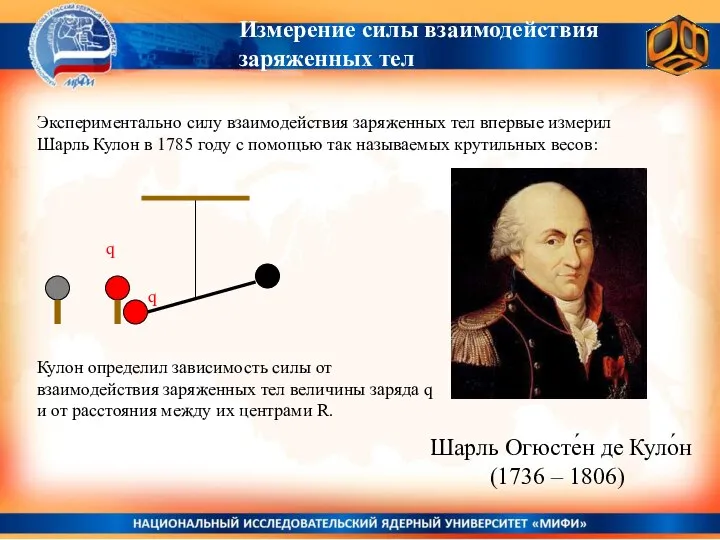
- 7. Измерение силы взаимодействия заряженных тел Экспериментально силу взаимодействия заряженных тел впервые измерил Шарль Кулон в 1785
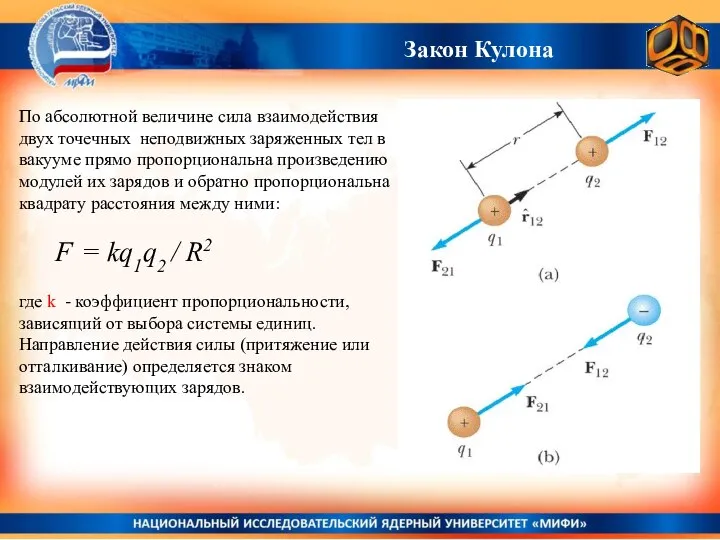
- 8. Закон Кулона По абсолютной величине сила взаимодействия двух точечных неподвижных заряженных тел в вакууме прямо пропорциональна
- 9. Закон Кулона. Единицы измерения заряда. В системе СИ коэффициент k численно равен силе взаимодействия двух единичных
- 10. Потенциальная энергия взаимодействия электрических зарядов. Закон Кулона F = kq1q2 / R2 математически очень похож на
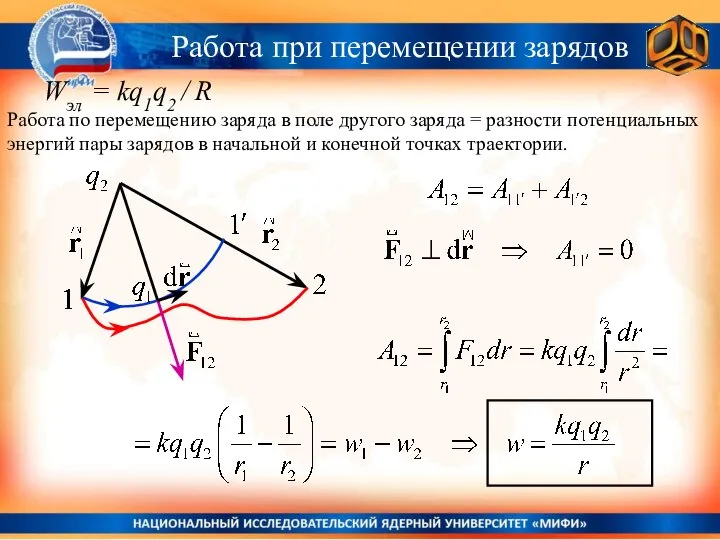
- 11. Работа при перемещении зарядов Wэл = kq1q2 / R Работа по перемещению заряда в поле другого
- 12. Электрическое поле. q Q Считается, что электрические заряды создают во всем окружающем пространстве “электрическое поле сил”,
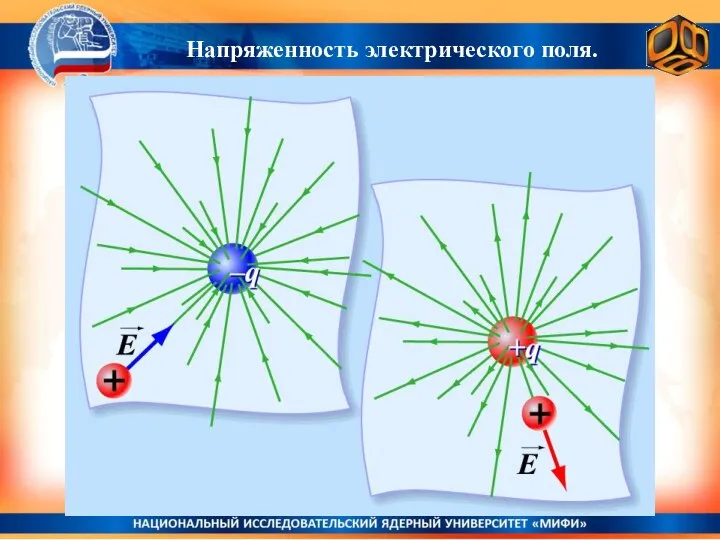
- 13. Напряженность электрического поля. q Q Величина, равная отношению силы, действующей на “пробный” заряд q, к величине
- 14. Напряженность электрического поля.
- 15. Суперпозиция электрических полей. Q1>0 Если в данной точке пространства электрические поля создаются несколькими зарядами, суммарная напряженность
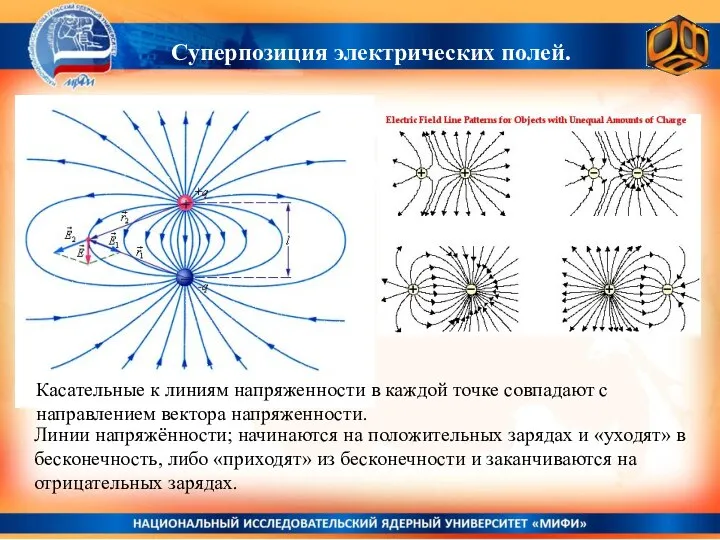
- 16. Суперпозиция электрических полей. Касательные к линиям напряженности в каждой точке совпадают с направлением вектора напряженности. Линии
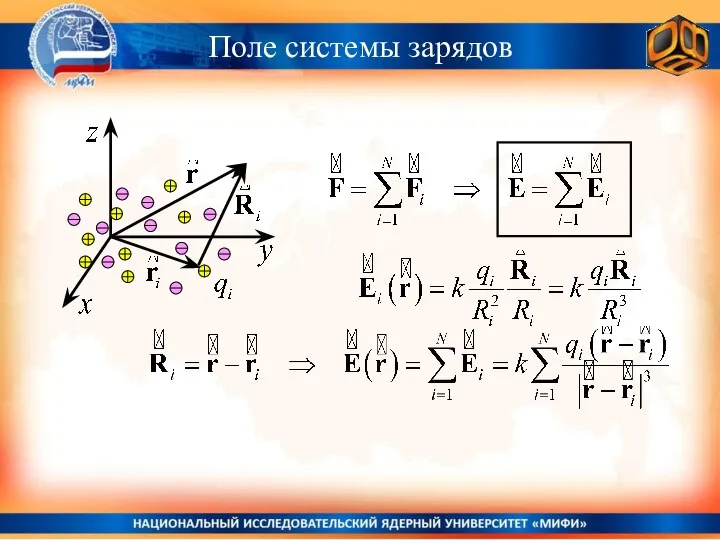
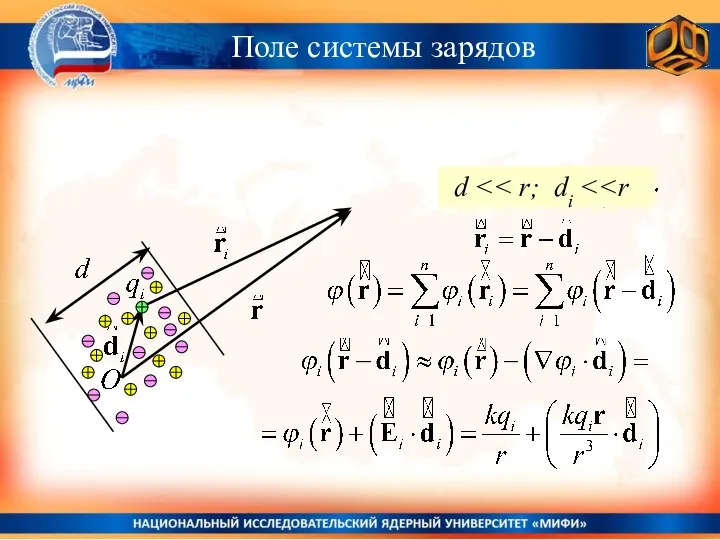
- 17. Поле системы зарядов
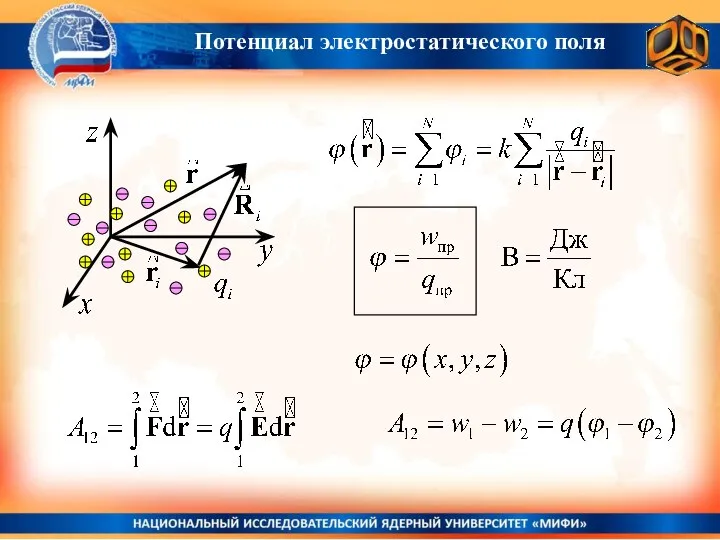
- 18. Потенциал электростатического поля
- 19. Напряжённость и потенциал Связь между напряжённостью электрического поля и потенциалом
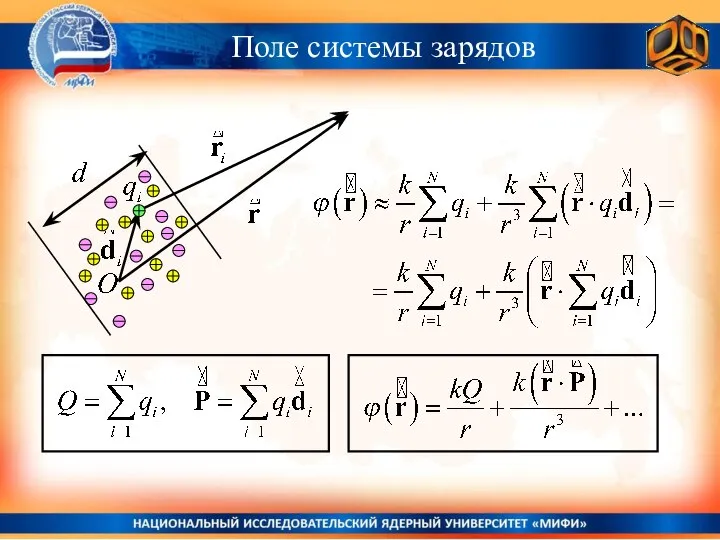
- 20. Поле системы зарядов Потенциальная энергия взаимодействия
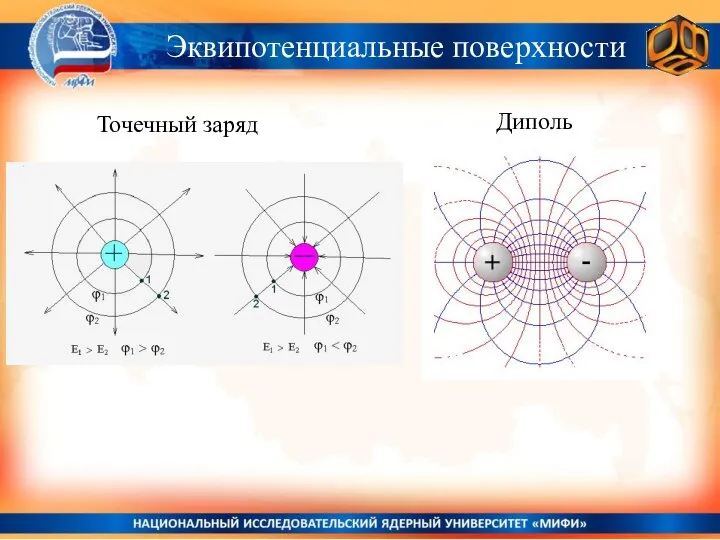
- 21. Эквипотенциальные поверхности и линии Поверхности, на которых потенциал принимает постоянное значение, называются эквипотенциальными поверхностями. Линии напряжённости
- 22. Эквипотенциальные поверхности Точечный заряд Диполь
- 23. Спасибо за внимание! Курс общей физики НИЯУ МИФИ Следующая лекция 15 сентября
- 24. Лекция 2 Электрическое поле точечного диполя. Диполь во внешнем электрическом поле Поле системы зарядов на больших
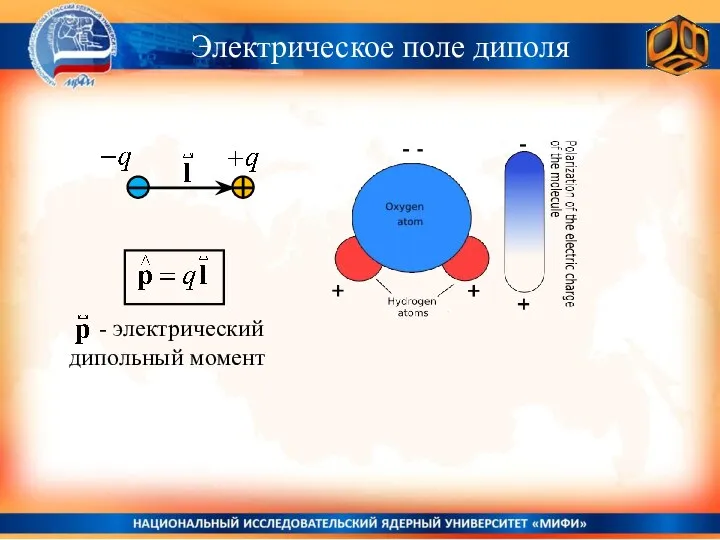
- 25. Электрическое поле диполя
- 26. Немного математики Приращение и дифференциал функции трёх переменных
- 27. Электрическое поле диполя = - +
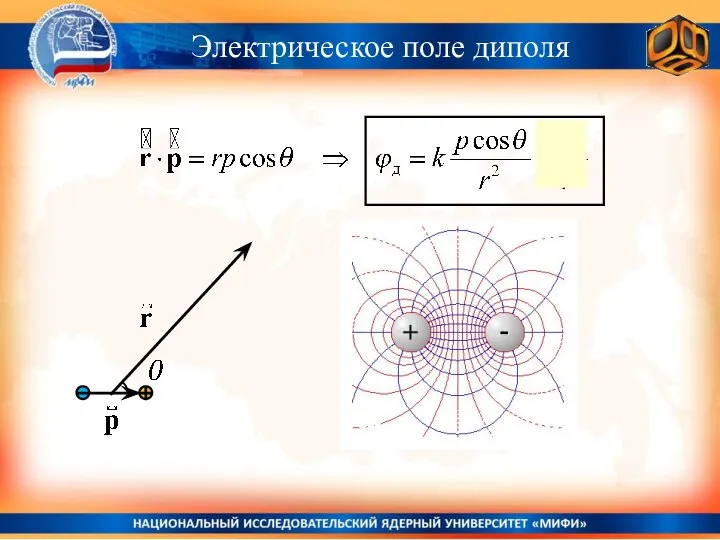
- 28. Электрическое поле диполя
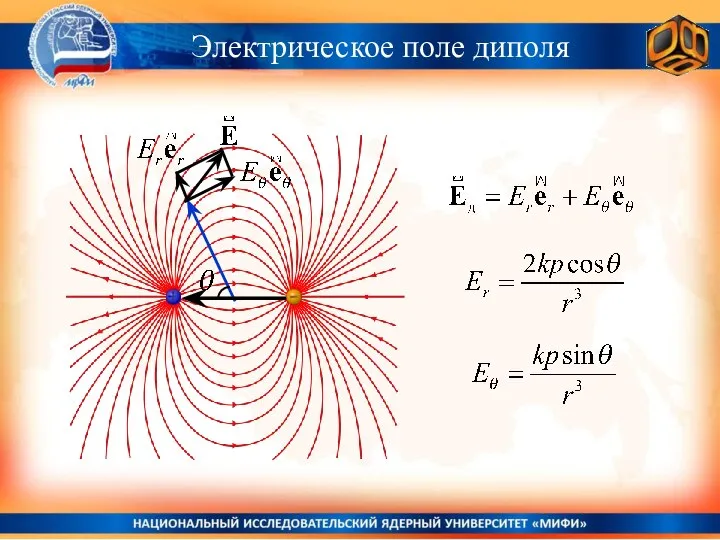
- 29. Напряжённость электрического поля диполя Электрическое поле диполя
- 30. Электрическое поле диполя
- 31. Спасибо за внимание! Курс общей физики НИЯУ МИФИ Следующая лекция 15 сентября
- 32. Диполь в электрическом поле Потенциальная энергия диполя во внешнем электрическом поле
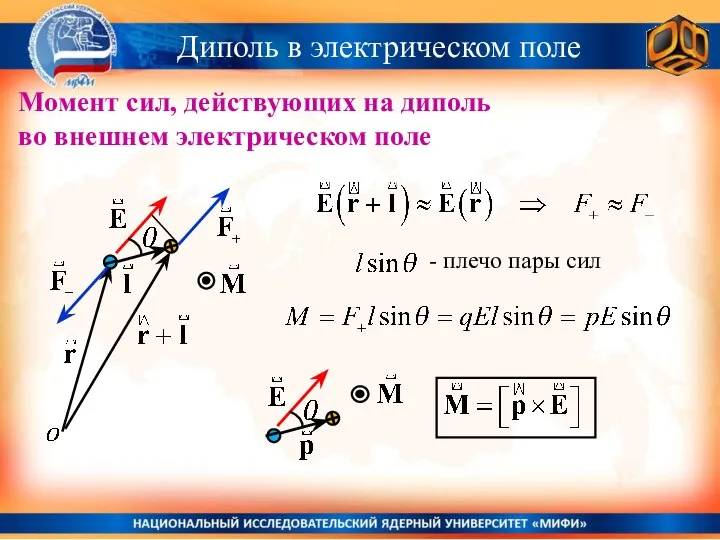
- 33. Момент сил, действующих на диполь во внешнем электрическом поле Диполь в электрическом поле
- 34. Диполь в электрическом поле Математическое дополнение. Приращение и дифференциал векторной функции трёх переменных
- 35. Сила, действующая на диполь во внешнем электрическом поле Диполь в электрическом поле Замечание: В статическом электрическом
- 36. Диполь в электрическом поле Пример 1. Однородное электрическое поле Пример 2. Слабо неоднородное электрическое поле
- 37. Поле системы зарядов d
- 38. Поле системы зарядов
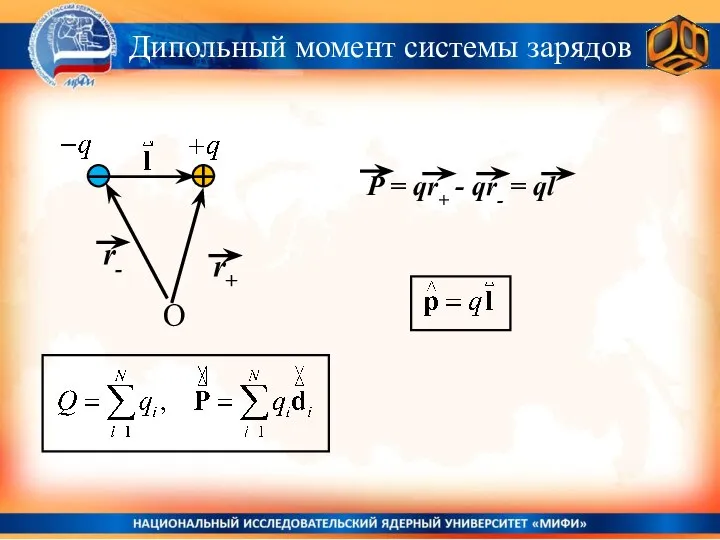
- 39. Дипольный момент системы зарядов O r- r+ P = qr+ - qr- = ql
- 41. Скачать презентацию























 Главные центральные оси сечения
Главные центральные оси сечения Колебания и волны (ОГЭ). Решение задач 9 класс
Колебания и волны (ОГЭ). Решение задач 9 класс Конденсатор
Конденсатор Силы осмоса. Как варить вкусную картошку
Силы осмоса. Как варить вкусную картошку Режим натуральной мощности
Режим натуральной мощности Закон сохранения энергии
Закон сохранения энергии Физические свойства металлов
Физические свойства металлов Линзы. Основные элементы
Линзы. Основные элементы Статика. Физика
Статика. Физика Волновая оптика
Волновая оптика Законы сохранения
Законы сохранения Алессандро Вольта - Электрическая батарея
Алессандро Вольта - Электрическая батарея Голография. Её физические принципы
Голография. Её физические принципы Управление параметрами излучения мультиферроиковой структуры электрическим полем
Управление параметрами излучения мультиферроиковой структуры электрическим полем Автономные инверторы
Автономные инверторы Гальванический элемент, полуэлемент, полуэлемент, е- Zn|Zn2+||Cu2+|Cu, анод, катод, - +, окисление, восстановление
Гальванический элемент, полуэлемент, полуэлемент, е- Zn|Zn2+||Cu2+|Cu, анод, катод, - +, окисление, восстановление Квалификационная работа Проект специализированной СТОА Honda на 5 рабочих постов с технологией замены топливного фильтра
Квалификационная работа Проект специализированной СТОА Honda на 5 рабочих постов с технологией замены топливного фильтра Испарение. Насыщенный и ненасыщенный пар. Поглощение энергии при испарении жидкости и выделение ее при конденсации пара
Испарение. Насыщенный и ненасыщенный пар. Поглощение энергии при испарении жидкости и выделение ее при конденсации пара Физика в картинках
Физика в картинках Основные приемы резания тонколистого металла и проволоки
Основные приемы резания тонколистого металла и проволоки Разветвленные цепи переменного тока
Разветвленные цепи переменного тока Презентация на тему Температура
Презентация на тему Температура  Двигатели технический систем
Двигатели технический систем Теплотехника. Основные определения и понятия. Параметры состояния. Уравнения состояния
Теплотехника. Основные определения и понятия. Параметры состояния. Уравнения состояния Презентация на тему Электромагнитная индукция
Презентация на тему Электромагнитная индукция  Явление самоиндукции
Явление самоиндукции Кинематика материальной точки. Тема №1
Кинематика материальной точки. Тема №1 Параметры эвольвентного зубчатого зацепления
Параметры эвольвентного зубчатого зацепления