Содержание
- 2. Лекция IV Свойства операторов и принцип неопределенности Гейзенберга
- 3. Собственной функцией Ψq, соответствующей собственному значению q оператора Q, называется функция, являющаяся решением уравнения
- 4. Свойства операторов, изображающих динамические переменные Какие операторы допустимы для изображения переменных?
- 5. I.1 Линейность операторов. I. Свойства операторов Любая динамическая переменная изображается линейным оператором Фредгольма 1 2
- 6. I. Свойства операторов Вещественная динамическая переменная классической механики в квантовой механике изображается самосопряженным или эрмитовым оператором!
- 7. I.2 Самосопряженность операторов Поскольку все значения q – вещественные q=q*, то ядро оператора - эрмитово: 3
- 8. II. Свойства собственных функций самосопряженных операторов II.1 Вещественность собственных значений Собственные значения эрмитовых операторов вещественны. 5
- 9. II.1 Вещественность собственных значений 6
- 10. Собственные функции эрмитовых операторов ортогональны: II. Свойства собственных функций самосопряженных операторов II.2 Ортогональность 7
- 11. II. Свойства собственных функций самосопряженных операторов II.2 Ортогональность
- 12. II. Свойства собственных функций самосопряженных операторов II.3 Собственные функции самосопряженных операторов – представляют состояния с фиксированным
- 13. Принцип неопределенности Когда измерения совместны?
- 14. III. Принцип неопределенности Пусть эрмитовы операторы связаны соотношением: Тогда имеет место следующее соотношение: 9 10
- 15. III. Принцип неопределенности 11
- 16. III. Принцип неопределенности 12
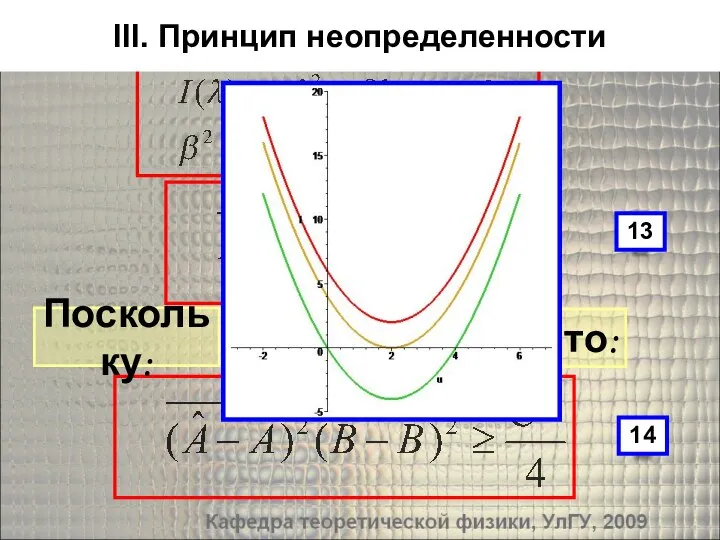
- 17. III. Принцип неопределенности Поскольку: то: 13 14
- 18. III. Принцип неопределенности Пример Операторы координаты и импульса 15
- 19. Пример Операторы координаты и импульса III. Принцип неопределенности 17 16
- 20. Свойства коммутирующих операторов Что означает коммутативность?
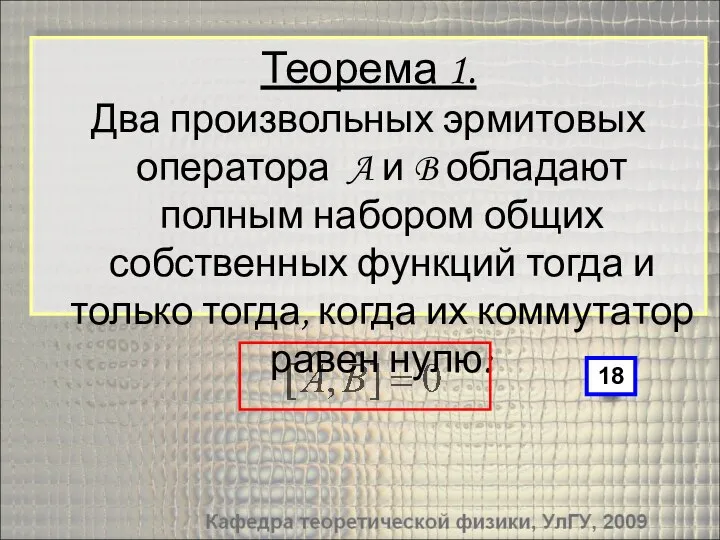
- 21. Теорема 1. Два произвольных эрмитовых оператора A и B обладают полным набором общих собственных функций тогда
- 22. Теорема I. Доказательство Прямое утверждение. Пусть операторы Обладают полным набором общих собственных функций: Тогда:
- 23. Поскольку это соотношение выполняется для всех функций базиса ψk, то отсюда следует, что коммутатор равен нулю
- 24. Теорема I. Доказательство Тогда пусть Ψk - собственные функции оператора A: Обратное утверждение. Пусть операторы коммутируют:
- 25. Теорема I. Доказательство Тогда функция Φk =BΨk удовлетворяет уравнению: Имеем:
- 26. Теорема I. Доказательство Отсюда: Следовательно : Следовательно собственные функции оператора A являются собственными функциями оператора B:
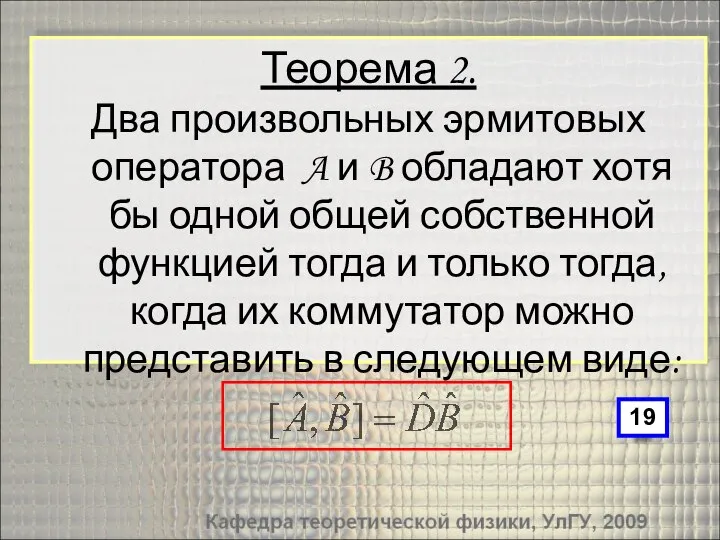
- 27. Теорема 2. Два произвольных эрмитовых оператора A и B обладают хотя бы одной общей собственной функцией
- 28. Теорема II. Доказательство Прямое утверждение. Пусть операторы обладают одной общей собственной функцией Ψ0: Тогда:
- 29. Поскольку любой оператор вида Теорема II. Доказательство действует так, что То всегда найдется оператор D такой
- 30. Теорема II. Доказательство Тогда пусть Ψ0 - собственная функция оператора B: Обратное утверждение. Пусть операторы удовлетворяют
- 31. Теорема II. Доказательство Следовательно функция Φ0 =AΨ0 удовлетворяет уравнению: Из (20) имеем: а из (21) получаем:
- 32. Теорема II. Доказательство Отсюда: Следовательно : Следовательно собственная функция Ψ0 оператора B является собственной функцией оператора
- 33. Теорема II. Следствие Из (20) имеем: Пусть Тогда:
- 34. Тогда функции Φk =BΨk являются собственными функциями оператора A1: Теорема II. Следствие 22 23
- 35. Пример Метод Дарбу
- 36. Рассмотрим следующие операторы: Пример. 24 Вычислим коммутатор:
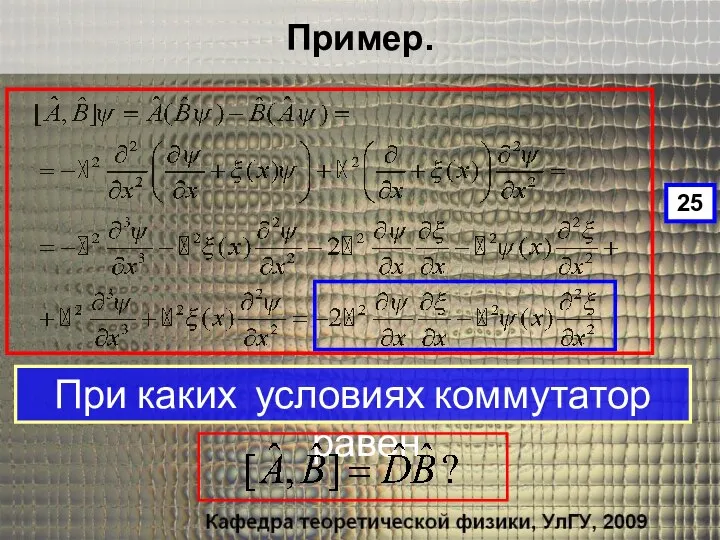
- 37. Пример. 25 При каких условиях коммутатор равен
- 38. Пример. 25
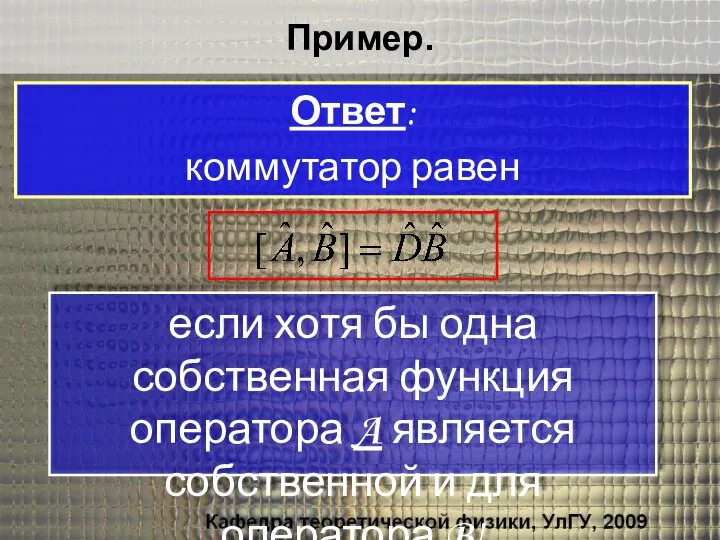
- 39. Пример. если хотя бы одна собственная функция оператора A является собственной и для оператора B! Ответ:
- 40. Пример. 26 27 Найдем собственные функции оператора A
- 41. Пример. 28
- 42. Пример. 29 Отсюда находим: Или: 30
- 43. Пример. 30 Результат: если Операторы A и B имеют одну общую собственную функцию и поэтому существует
- 44. Пример. Вычислим оператор D. Будем искать его в виде оператора умножения на функцию 31
- 45. Пример. Тогда 32 Отсюда
- 46. Пример. I Отсюда следует: II 33 34 35
- 47. Пример. Окончательно: 36
- 48. Пример. 37
- 49. Пример. Являются функции: 38
- 50. Пример. Окончательно, функции Являются собственными функциями A1 39 40
- 51. Следующая лекция Стационарное уравнение Шредингера
- 53. Скачать презентацию









































 Демонтаж рулевого управления автомобиля
Демонтаж рулевого управления автомобиля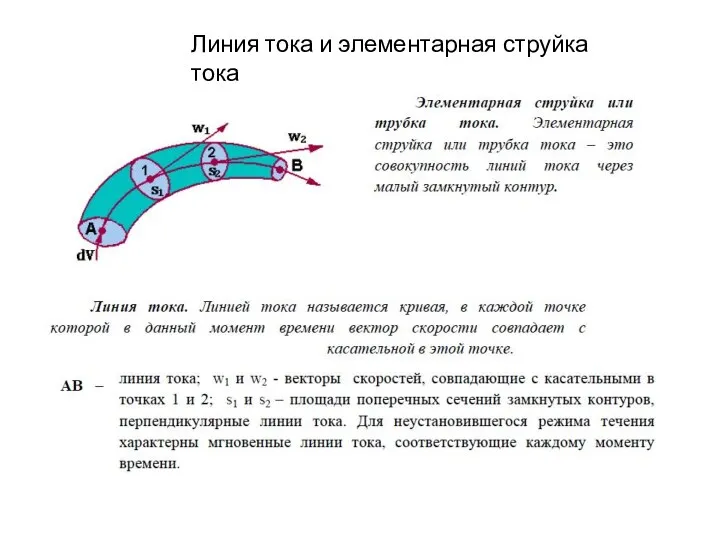 2.Уравнение Бернулли. Давление жидкости на плоские и криволинейные поверхности
2.Уравнение Бернулли. Давление жидкости на плоские и криволинейные поверхности Me-полупроводник
Me-полупроводник Электрический ток в различных средах
Электрический ток в различных средах Отбойный молоток
Отбойный молоток Описание электрического поля
Описание электрического поля Распределение работ по текущему ремонту автомобилей на постовые и участковые
Распределение работ по текущему ремонту автомобилей на постовые и участковые Проставка на раму
Проставка на раму Презентация на тему Первоначальные сведения о строении вещества
Презентация на тему Первоначальные сведения о строении вещества  Воздухоплавание
Воздухоплавание Значение режима смазывания для увеличения долговечности работы машин и механизмов
Значение режима смазывания для увеличения долговечности работы машин и механизмов Энергетические установки в космосе
Энергетические установки в космосе Осевое растяжение и сжатие стержней
Осевое растяжение и сжатие стержней Кинематика плоскопараллельного движения абсолютно твердого тела и сложного движения точки
Кинематика плоскопараллельного движения абсолютно твердого тела и сложного движения точки Логические элементы
Логические элементы Источники света. Прямолинейное распространение света
Источники света. Прямолинейное распространение света Презентация на тему Электрическая цепь
Презентация на тему Электрическая цепь  Презентация OpenDocument
Презентация OpenDocument Схема Кирпатрика-Баеза
Схема Кирпатрика-Баеза Презентация на тему Плавание судов и воздухоплавание
Презентация на тему Плавание судов и воздухоплавание  Однородное и неоднородное магнитное поле
Однородное и неоднородное магнитное поле Применение ядерной энергии в различных отраслях. Доза радиоактивного излучения
Применение ядерной энергии в различных отраслях. Доза радиоактивного излучения Назначение релейной защиты
Назначение релейной защиты Ядерные реакции
Ядерные реакции Презентация на тему Сложение сил, направленных вдоль одной прямой. Равнодействующая сила
Презентация на тему Сложение сил, направленных вдоль одной прямой. Равнодействующая сила  Сила трения. Ответы к заданию №1
Сила трения. Ответы к заданию №1 Курс физики в домашней школе Фоксфорд
Курс физики в домашней школе Фоксфорд Простые механизмы. Рычаг
Простые механизмы. Рычаг