Содержание
- 2. Структура курса и формы работы Лекции Лабораторные работы Решение задач САМОСТОЯТЕЛЬНАЯ работа Механика Молекулярная физика и
- 3. Балльно-рейтинговая система Аудиторная активность: Лекции (за каждую лекцию) посещение, конспект – 0,5 балла активная работа, ответы
- 4. Что важно при работе с информацией не только слУшать, но слЫшать уметь читать – понимать прочитанный
- 5. Колебания и волны Колебания Гармонические колебания Сложение колебаний Затухающие колебания Вынужденные колебания Волны упругие волны электромагнитные
- 6. Структура раздела Классификация колебаний Гармонические колебания Сложение колебаний Влияние внешних сил на колебания Энергия колебаний Гармонические
- 7. Колебания в природе и технике Физическая природа колебаний: Механические колебания Электромагнитные колебания биологические колебания … Сердце
- 8. Классификация колебаний По физической природе и типу колеблющейся величины звук свет
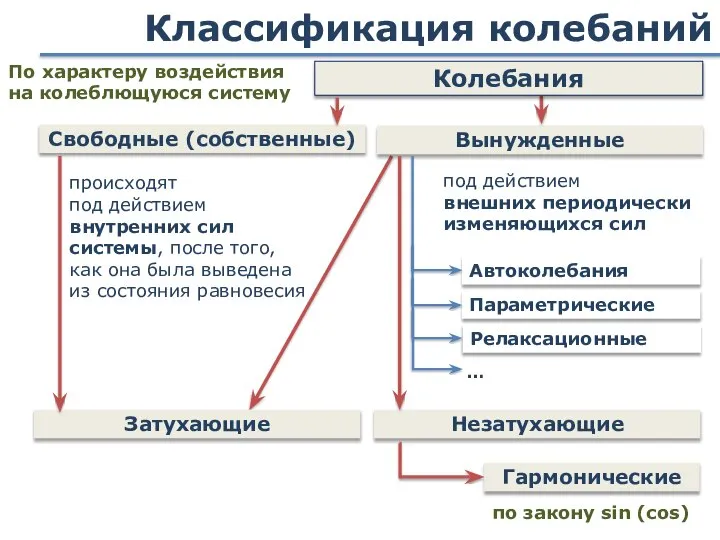
- 9. Классификация колебаний Автоколебания Свободные (собственные) Вынужденные Затухающие Гармонические происходят под действием внутренних сил системы, после того,
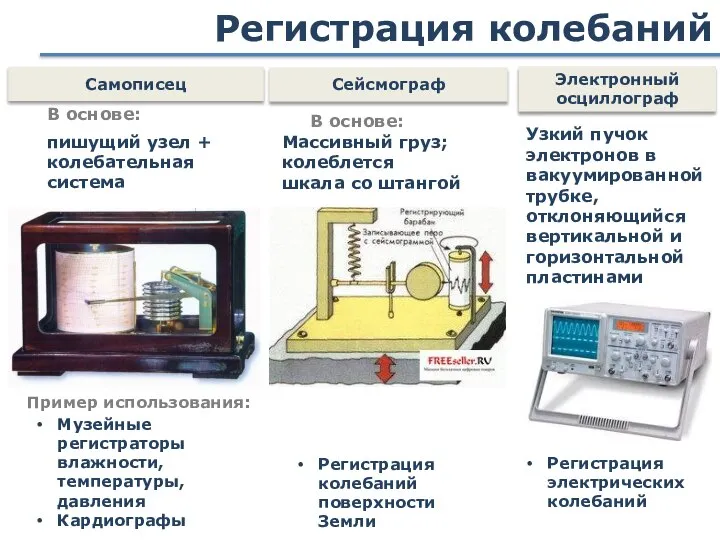
- 10. Регистрация колебаний Самописец В основе: пишущий узел + колебательная система Музейные регистраторы влажности, температуры, давления Кардиографы
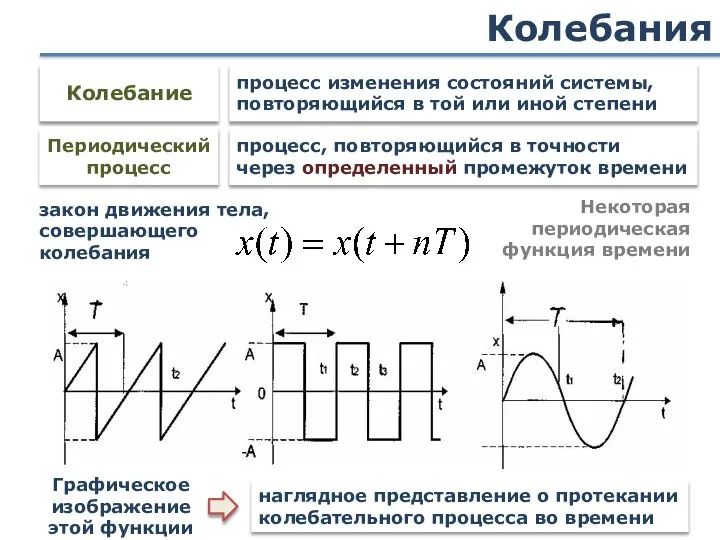
- 11. Колебания закон движения тела, совершающего колебания Некоторая периодическая функция времени Графическое изображение этой функции наглядное представление
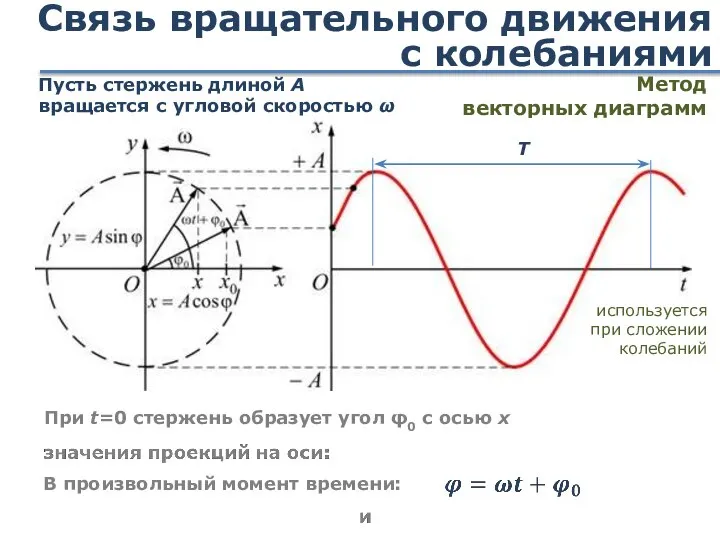
- 12. Связь вращательного движения с колебаниями Пусть стержень длиной А вращается с угловой скоростью ω При t=0
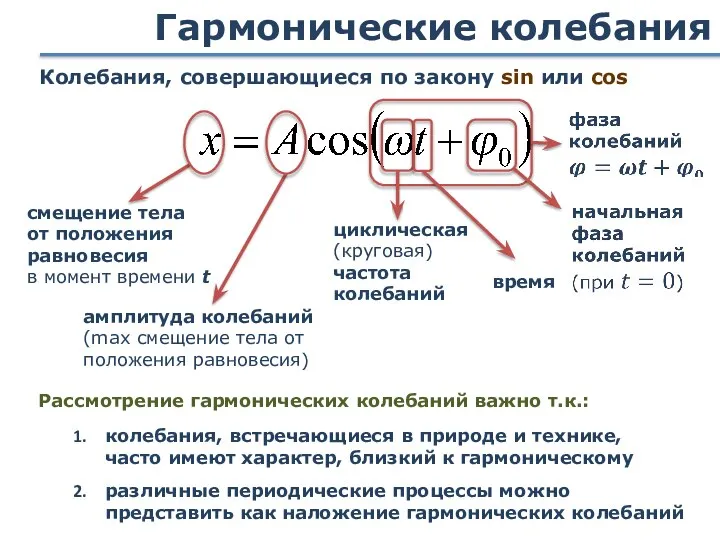
- 13. Гармонические колебания Колебания, совершающиеся по закону sin или cos смещение тела от положения равновесия в момент
- 14. Характеристики колебательного движения смещение тела от положения равновесия Амплитуда колебаний циклическая (круговая) частота колебаний время колебаний
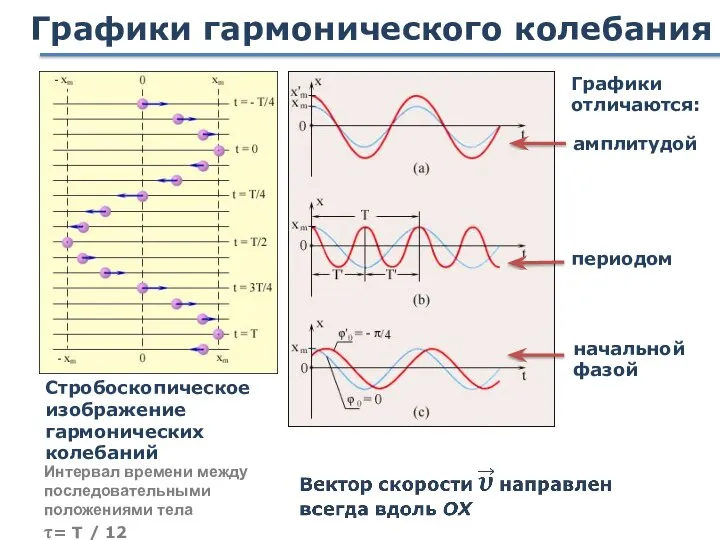
- 15. Графики гармонического колебания Стробоскопическое изображение гармонических колебаний амплитудой Графики отличаются: периодом начальной фазой Интервал времени между
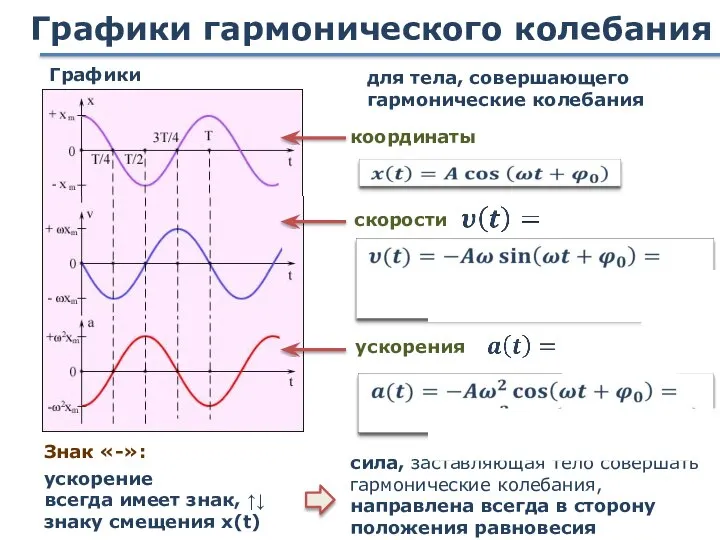
- 16. Графики гармонического колебания Графики ускорения координаты скорости для тела, совершающего гармонические колебания Знак «-»: сила, заставляющая
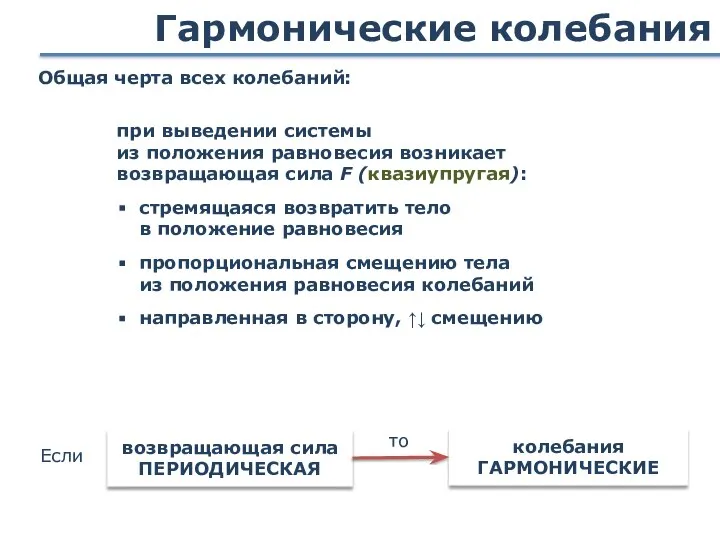
- 17. Гармонические колебания Общая черта всех колебаний: при выведении системы из положения равновесия возникает возвращающая сила F
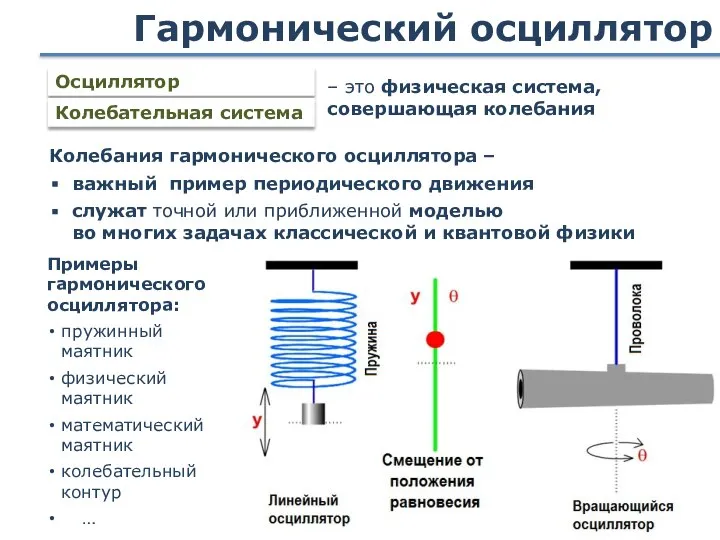
- 18. Гармонический осциллятор Осциллятор Колебания гармонического осциллятора – важный пример периодического движения служат точной или приближенной моделью
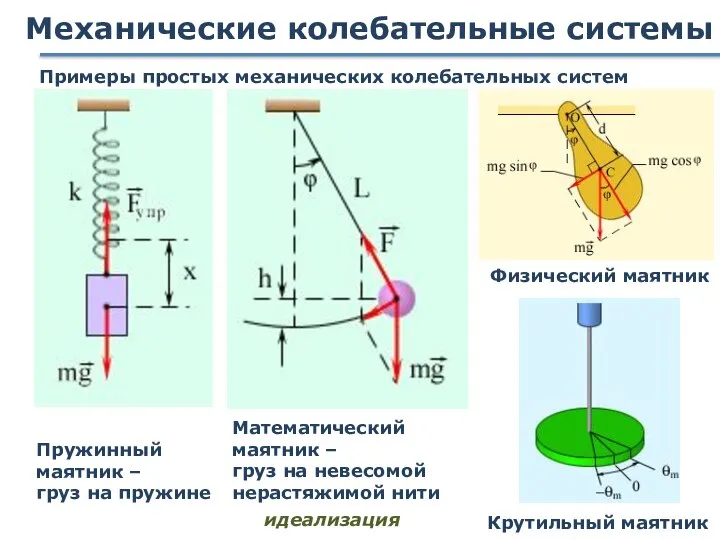
- 19. Механические колебательные системы Примеры простых механических колебательных систем Пружинный маятник – груз на пружине Математический маятник
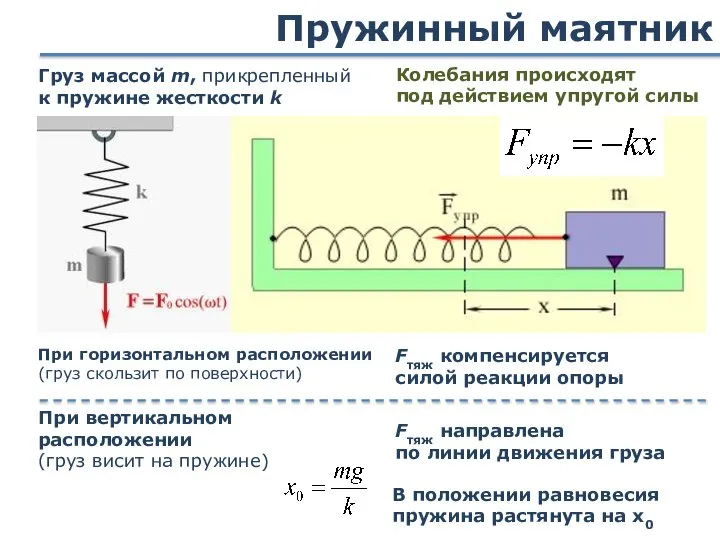
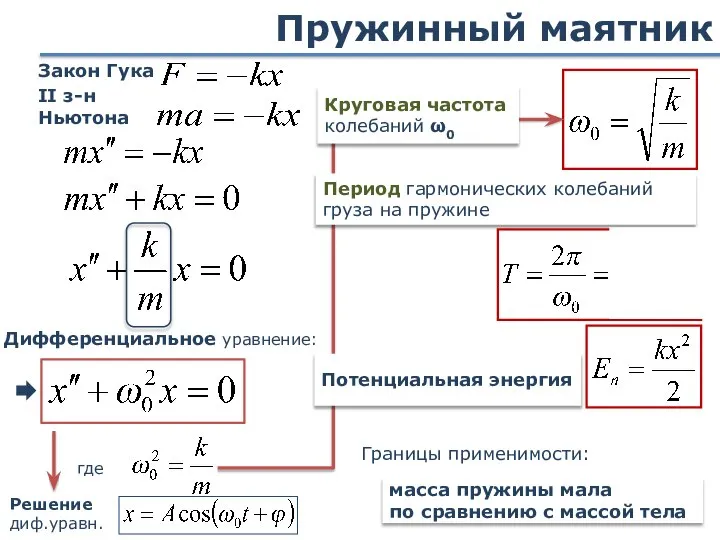
- 20. Пружинный маятник Груз массой m, прикрепленный к пружине жесткости k При горизонтальном расположении (груз скользит по
- 21. Пружинный маятник масса пружины мала по сравнению с массой тела Границы применимости: Период гармонических колебаний груза
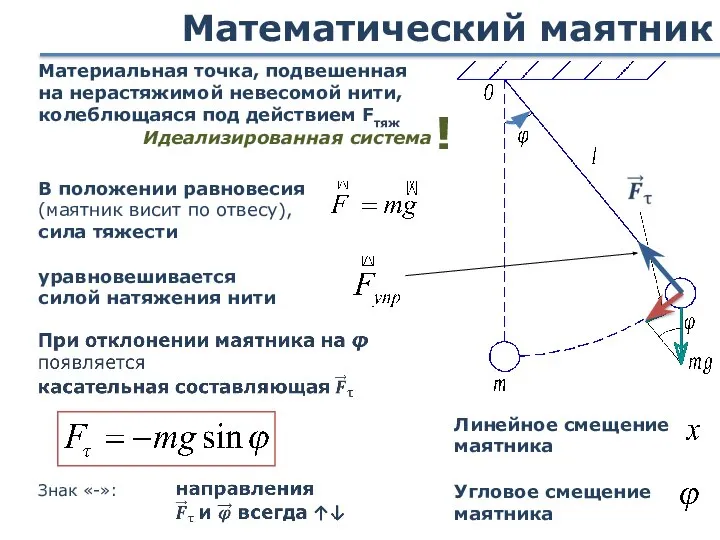
- 22. Математический маятник Материальная точка, подвешенная на нерастяжимой невесомой нити, колеблющаяся под действием Fтяж Идеализированная система !
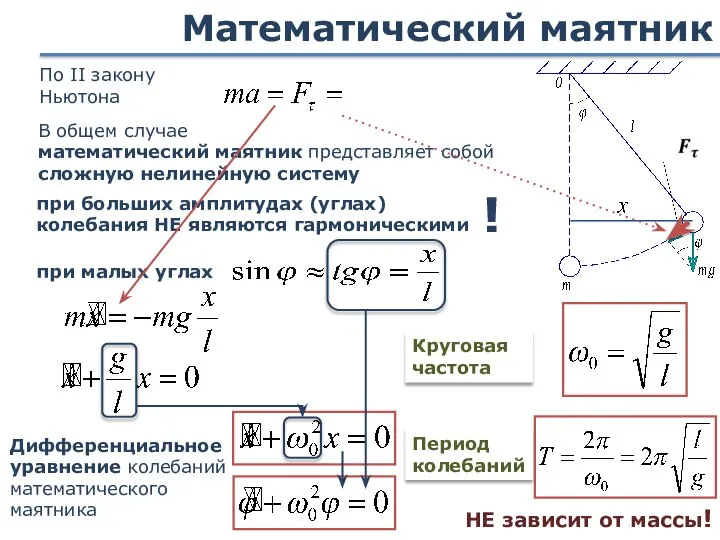
- 23. Математический маятник По II закону Ньютона при малых углах В общем случае математический маятник представляет собой
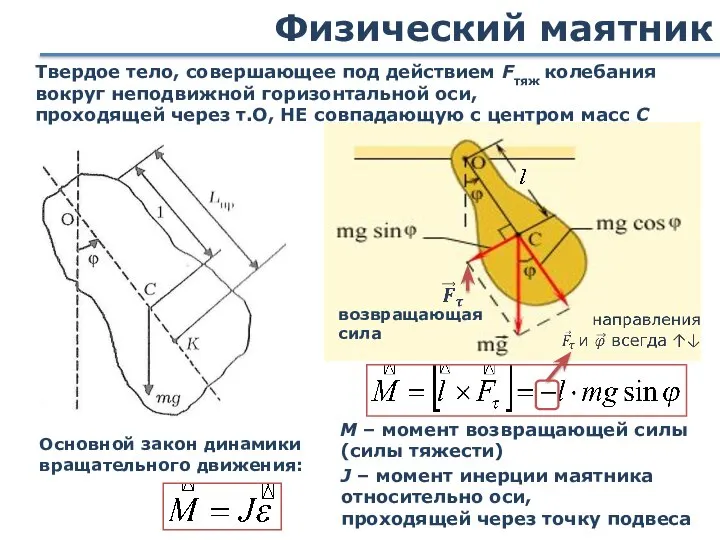
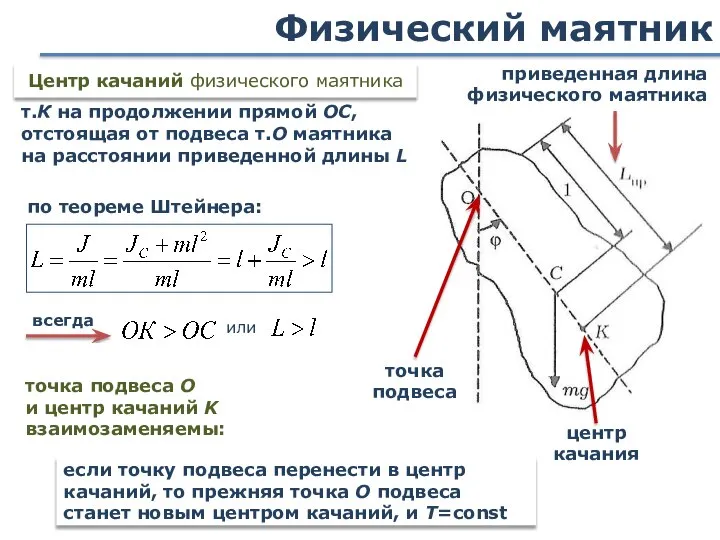
- 24. Физический маятник Твердое тело, совершающее под действием Fтяж колебания вокруг неподвижной горизонтальной оси, проходящей через т.О,
- 25. Физический маятник Основной закон динамики вращательного движения для малых углов Период колебаний Круговая частота приведенная длина
- 26. Физический маятник т.К на продолжении прямой ОС, отстоящая от подвеса т.О маятника на расстоянии приведенной длины
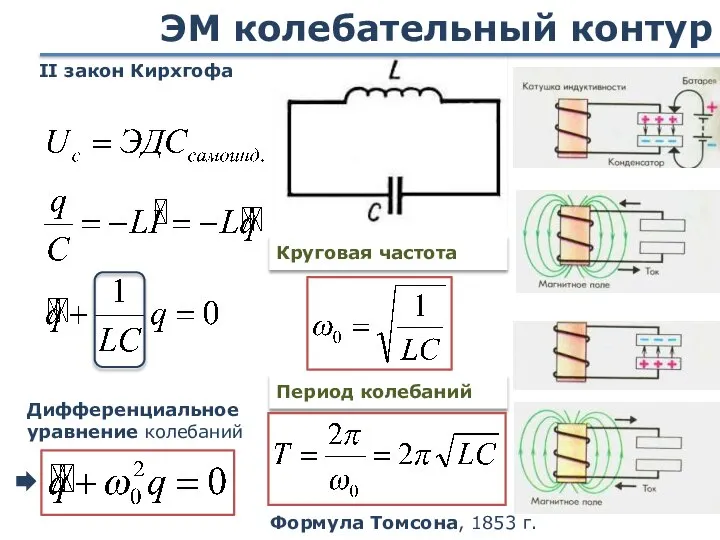
- 27. ЭМ колебательный контур II закон Кирхгофа Дифференциальное уравнение колебаний Период колебаний Круговая частота Формула Томсона, 1853
- 28. Уильям Томсон, лорд Кельвин Британский физик и механик Основные работы в области термодинамики, механики, электродинамики В
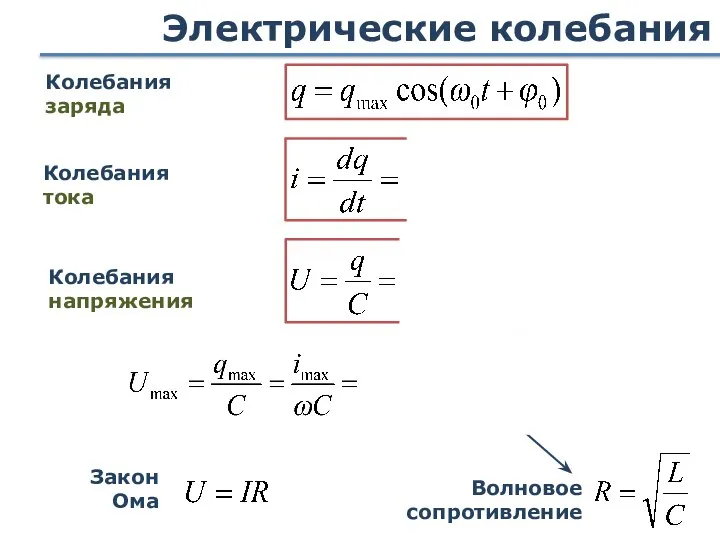
- 29. Электрические колебания Колебания заряда Колебания тока Колебания напряжения Закон Ома Волновое сопротивление
- 30. Волновое сопротивление Волновое сопротивление линии передач - амплитуда напряжения волны (падающей, отраженной или бегущей) - амплитуда
- 31. Гармонический осциллятор Итак, дифференциальное уравнение гармонического осциллятора: Решение этого уравнения: Уравнение гармонических колебаний Другие виды записи
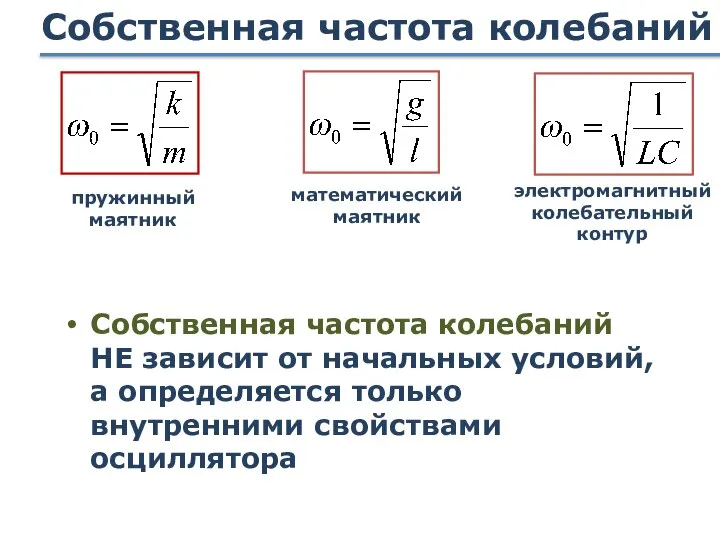
- 32. Собственная частота колебаний От каких параметров зависит собственная частота колебаний? пружинный маятник математический маятник электромагнитный колебательный
- 33. Квазиупругие силы Чтобы система совершала гармонические колебания необходимо и достаточно, чтобы единственная сила, действующая в ней
- 34. Контрольные вопросы Как изменится период колебаний пружинного маятника при увеличении массы груза в два раза? Период
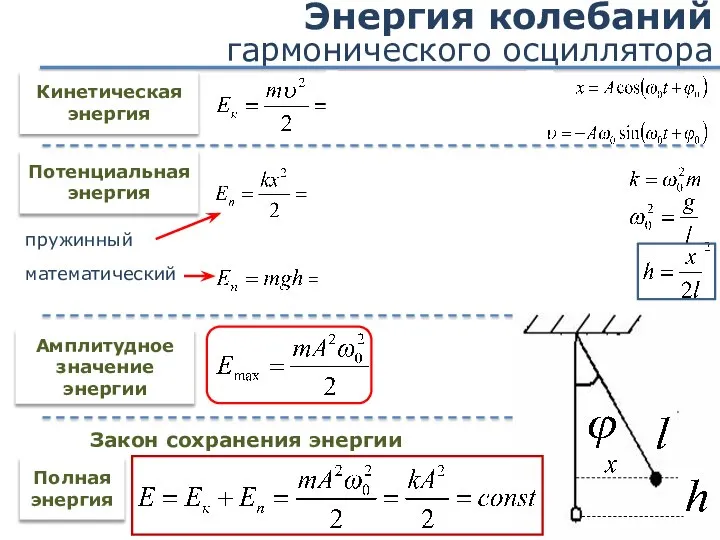
- 35. Энергия колебаний гармонического осциллятора Кинетическая энергия Потенциальная энергия Полная энергия Закон сохранения энергии Амплитудное значение энергии
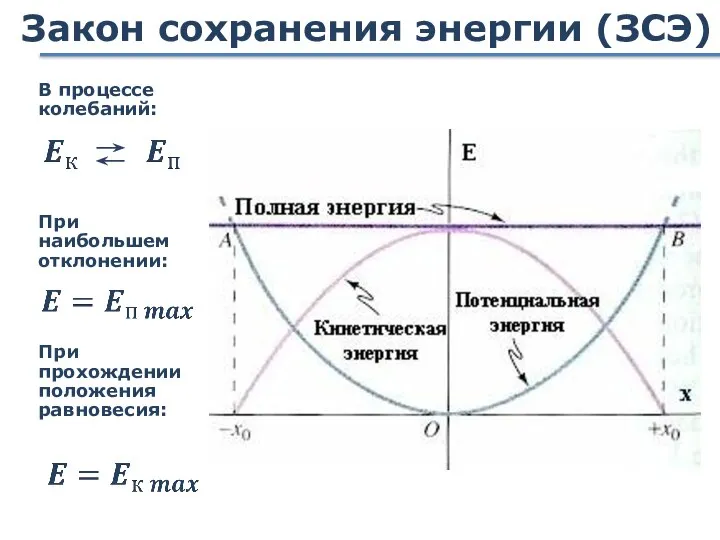
- 36. Закон сохранения энергии (ЗСЭ) В процессе колебаний: При наибольшем отклонении: При прохождении положения равновесия:
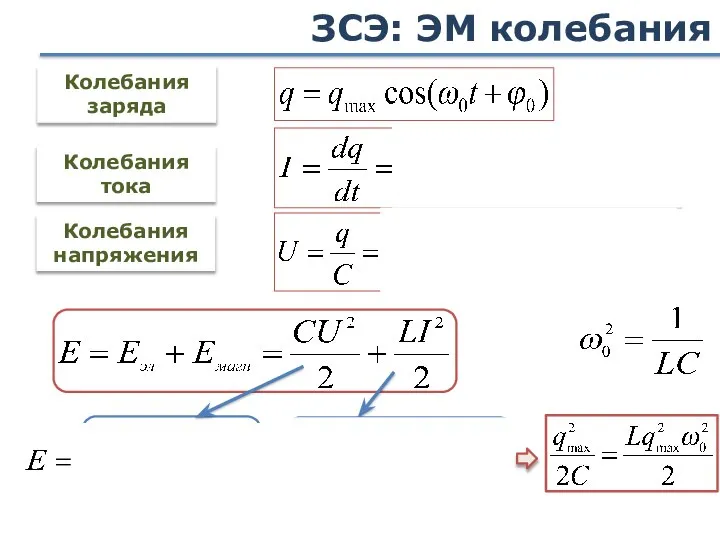
- 37. ЗСЭ: ЭМ колебания Колебания заряда Колебания тока Колебания напряжения
- 38. Энергетическая характеристика колебаний Интенсивность колебаний I средняя энергия колебаний за период Средняя кинетическая энергия Средняя потенциальная
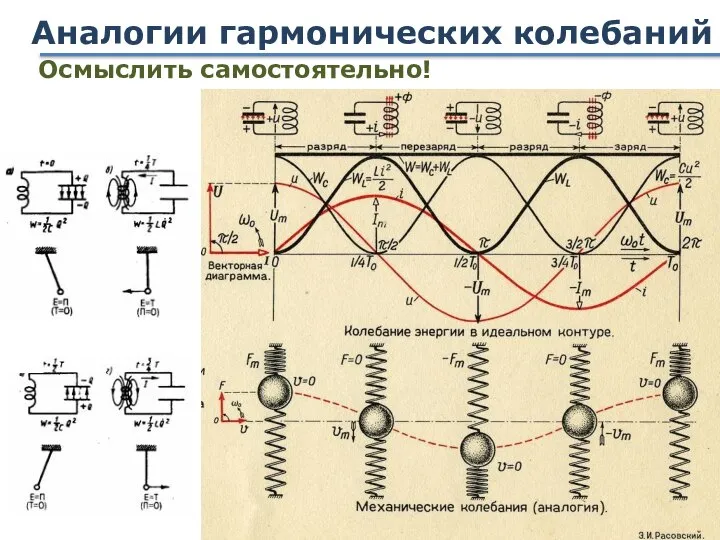
- 39. Аналогии гармонических колебаний Осмыслить самостоятельно!
- 40. Контрольный вопрос и задача От чего зависит энергия колебательной системы? Определить отношение кинетической энергии точки, совершающей
- 41. Сложение колебаний
- 42. Сложение колебаний Сложение колебаний одинакового направления удобно проводить с помощью метода векторных диаграмм Амплитуда 1. Начальная
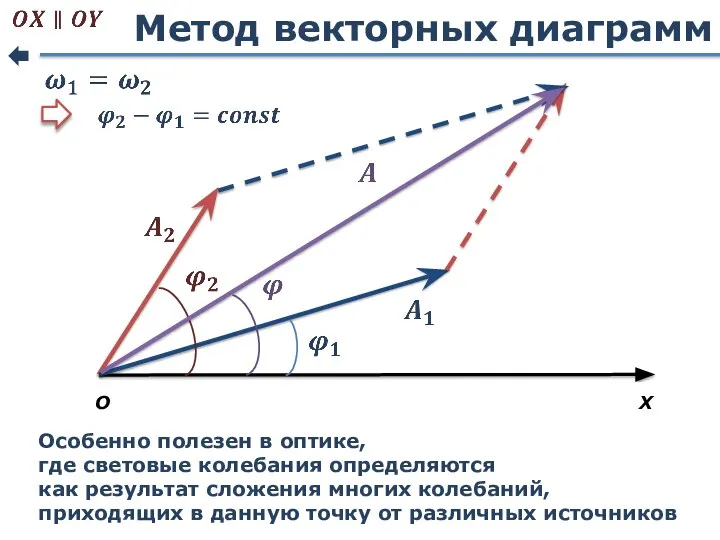
- 43. Метод векторных диаграмм X О Особенно полезен в оптике, где световые колебания определяются как результат сложения
- 44. Сложение колебаний в одной фазе Колебания одинакового направления 1. т.е. Амплитуда Условие МАКСИМУМА Колебания усиливают друг
- 45. Сложение колебаний в противофазе Колебания одинакового направления т.е. Амплитуда Условие МИНИМУМА Колебания ослабляют друг друга НЕчетное
- 46. Сложение колебаний Частоты складываемых колебаний мало отличаются Результирующее колебание: биения Частота биений можно рассматривать как гармоническое
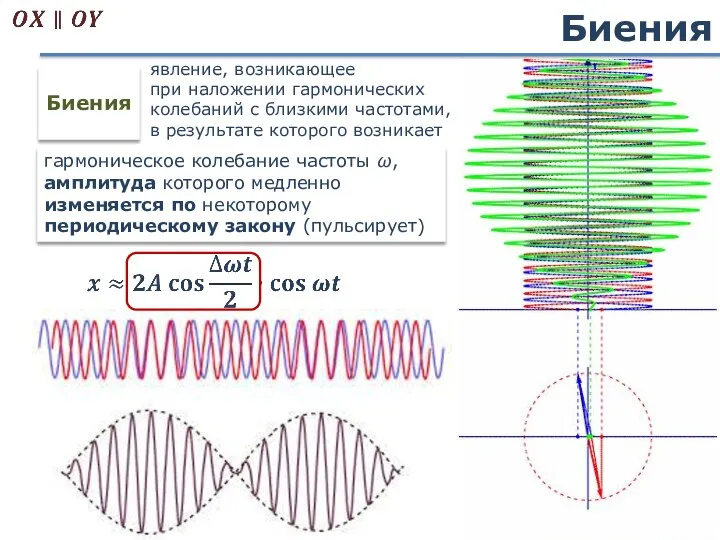
- 47. Биения Биения гармоническое колебание частоты ω, амплитуда которого медленно изменяется по некоторому периодическому закону (пульсирует) явление,
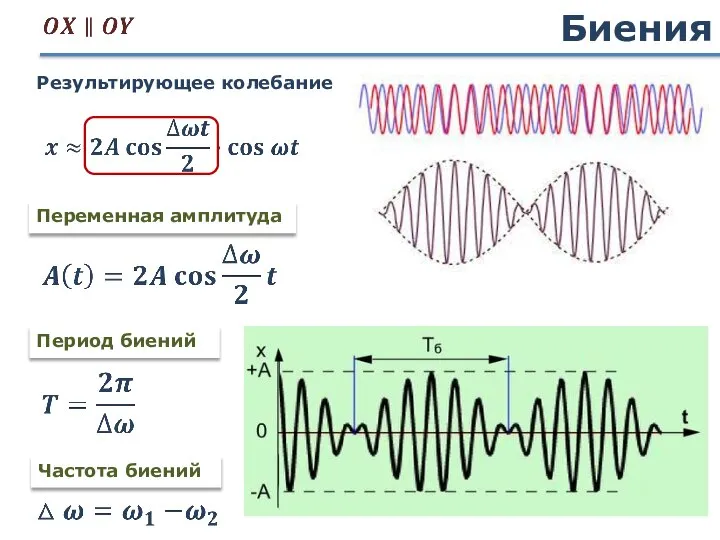
- 48. Биения Частота биений Переменная амплитуда Период биений Результирующее колебание
- 49. Сложение колебаний Колебания одинакового направления (Система с ОДНОЙ степенью свободы) величина и скорость вращения суммарного вектора
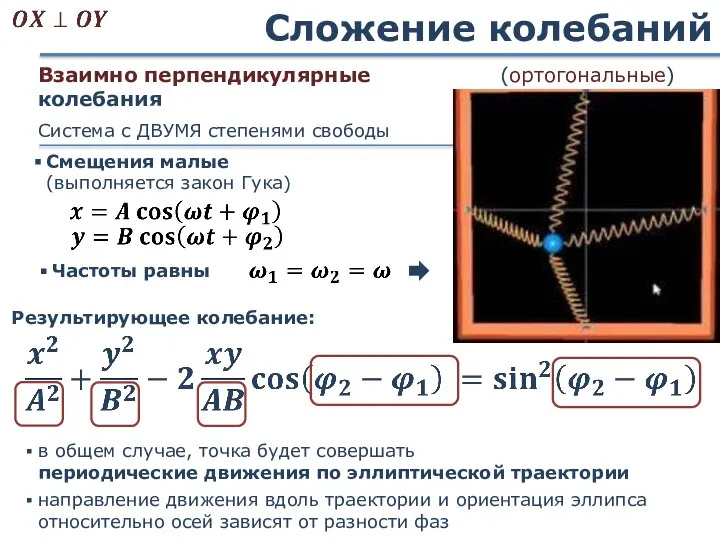
- 50. Сложение колебаний Взаимно перпендикулярные колебания Результирующее колебание: в общем случае, точка будет совершать периодические движения по
- 51. Сложение колебаний (вывод уравнения) после преобразований получим:
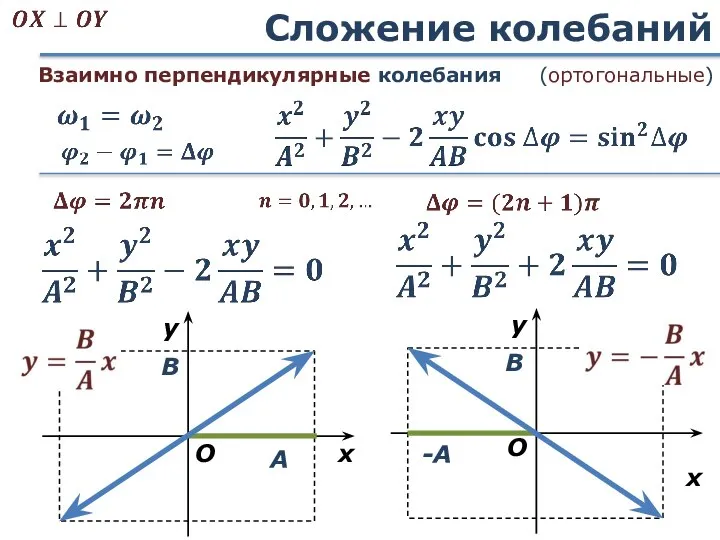
- 52. Сложение колебаний Взаимно перпендикулярные колебания (ортогональные)
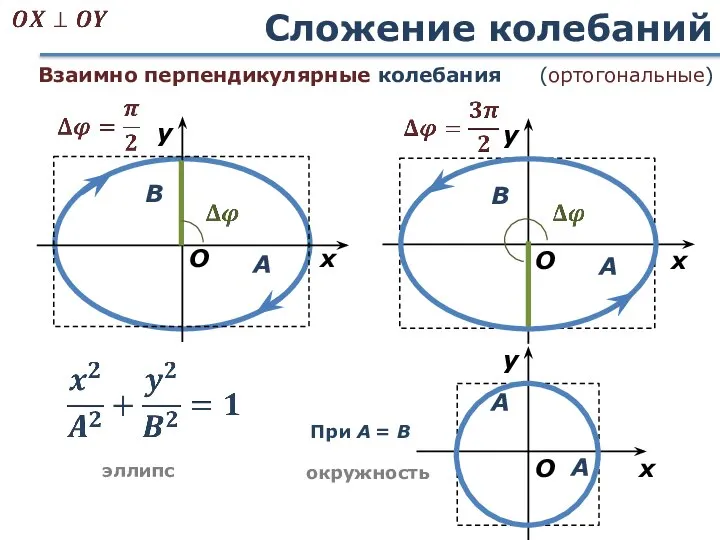
- 53. Сложение колебаний При А = B эллипс окружность Взаимно перпендикулярные колебания (ортогональные)
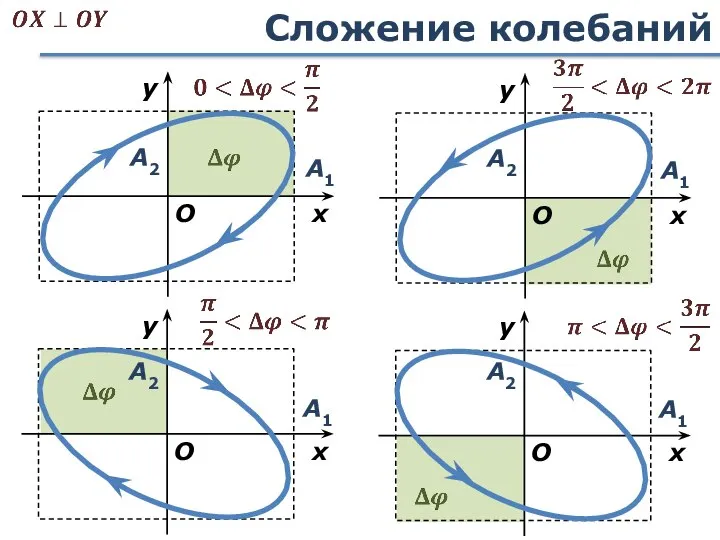
- 54. Сложение колебаний А1 x y O А2
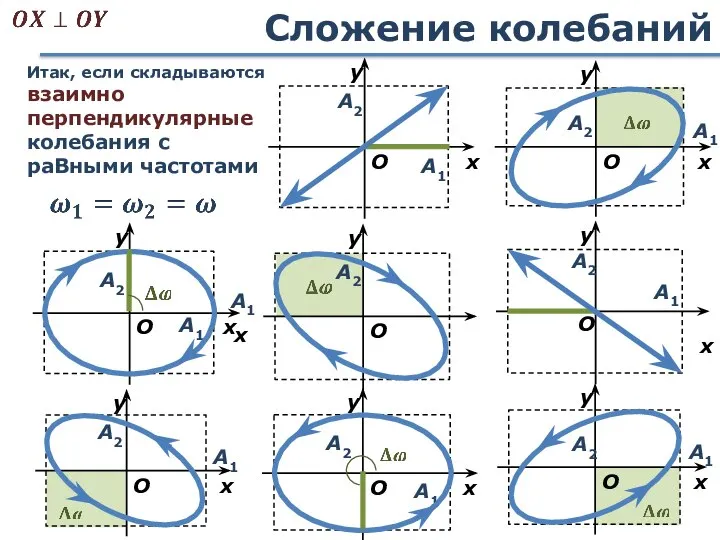
- 55. Сложение колебаний А1 x Итак, если складываются взаимно перпендикулярные колебания с раВными частотами
- 56. Сложение колебаний Взаимно перпендикулярные колебания с раЗными частотами где m, n – целые числа (частоты кратны
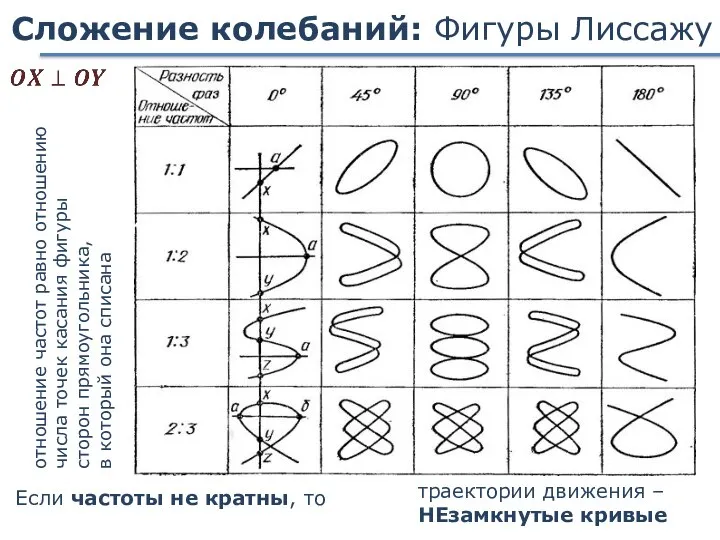
- 57. Сложение колебаний: Фигуры Лиссажу Если частоты не кратны, то траектории движения – НЕзамкнутые кривые отношение частот
- 58. Задачи Точка участвует одновременно в двух гармонических колебаниях, происходящих во взаимно перпендикулярных направлениях и описываемых уравнениями:
- 59. Затухающие колебания
- 60. Затухающие колебания Уменьшение амплитуды колебания ведет к потере энергии, т.к. Свободные колебания с уменьшающейся амплитудой называют
- 61. Дифференциальное уравнение затухающих колебаний Дифференциальное уравнение затухающих колебаний пружинного маятника в вязкой среде Разделим на m
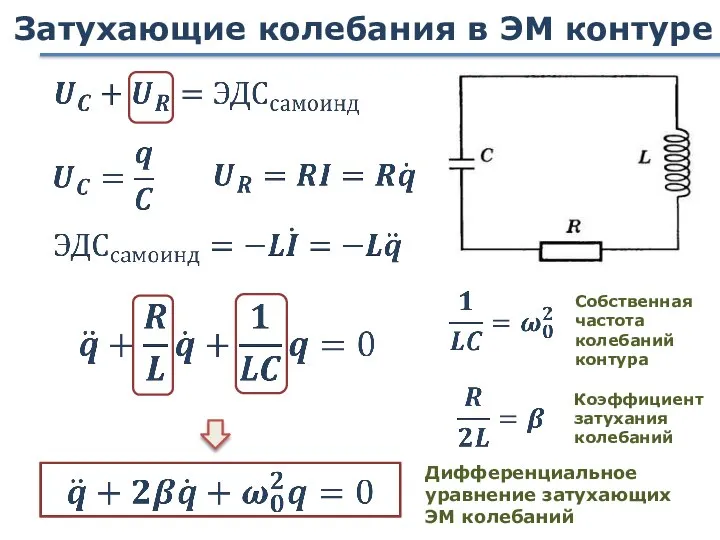
- 62. Затухающие колебания в ЭМ контуре Дифференциальное уравнение затухающих ЭМ колебаний Собственная частота колебаний контура Коэффициент затухания
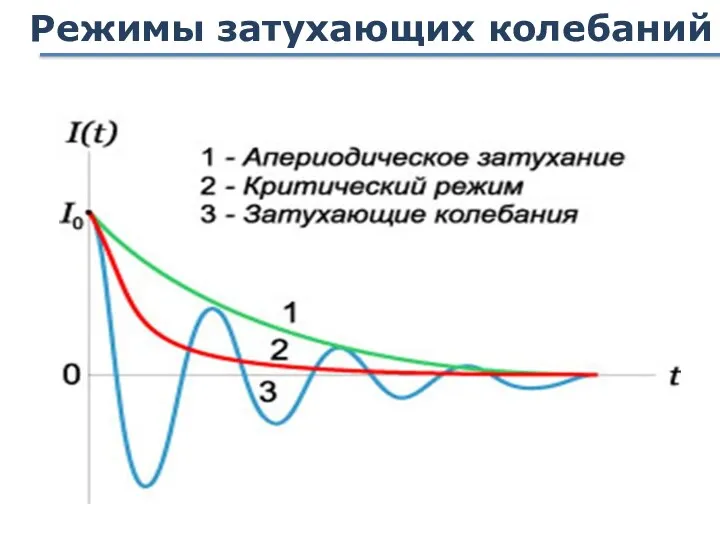
- 63. Решение дифференциального уравнения затухающих колебаний В зависимости от соотношения между собственной частотой системы и коэффициентом затухания
- 64. Параметры затухающих колебаний Частота затухающих колебаний Амплитуда затухающих колебаний Начальная амплитуда Период затухающих колебаний Время релаксации
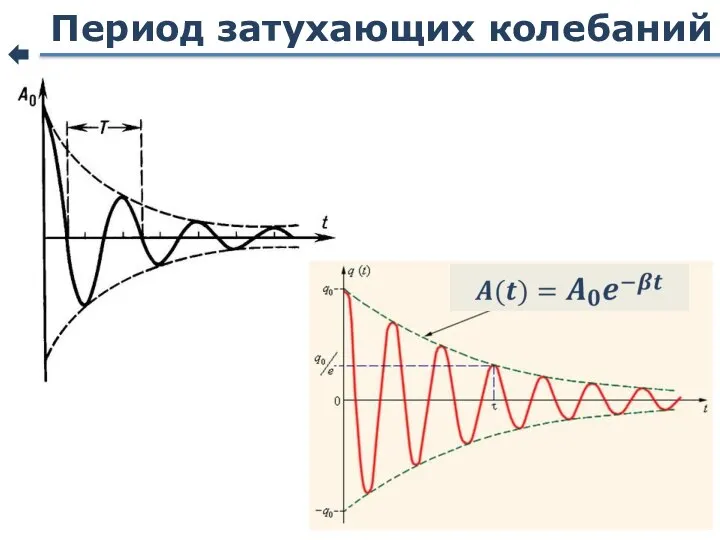
- 65. Период затухающих колебаний
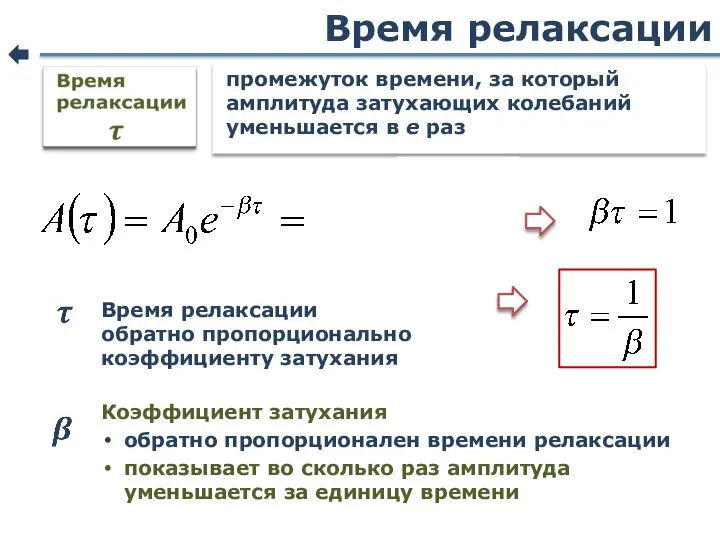
- 66. Время релаксации промежуток времени, за который амплитуда затухающих колебаний уменьшается в е раз Коэффициент затухания обратно
- 67. Логарифмический декремент затухания натуральный логарифм двух последовательных амплитуд Характеризует степень затухания – показывает за какое количество
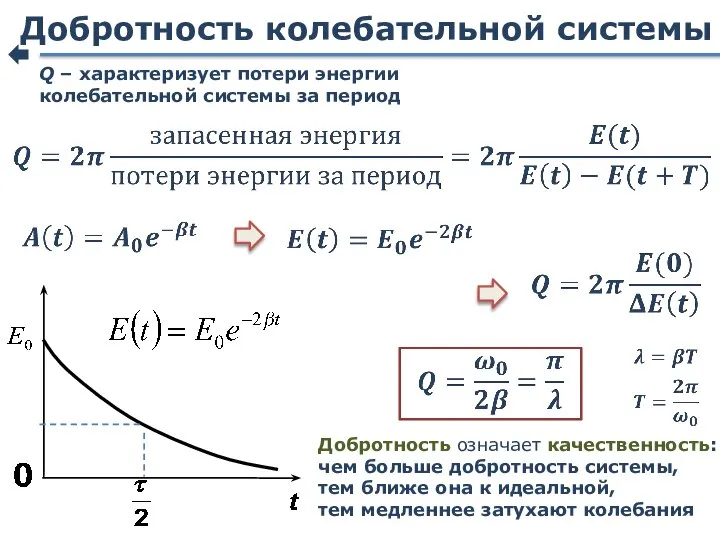
- 68. Добротность колебательной системы Q – характеризует потери энергии колебательной системы за период Добротность означает качественность: чем
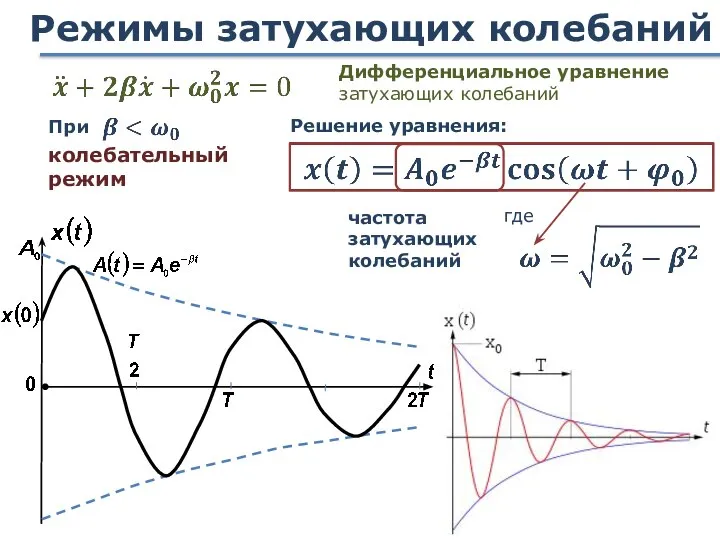
- 69. Режимы затухающих колебаний Дифференциальное уравнение затухающих колебаний Решение уравнения: где частота затухающих колебаний колебательный режим При
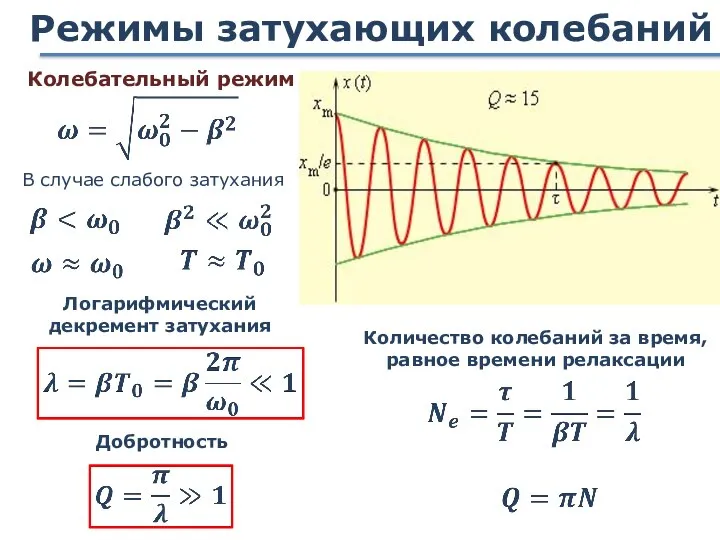
- 70. Режимы затухающих колебаний В случае слабого затухания Колебательный режим Логарифмический декремент затухания Добротность Количество колебаний за
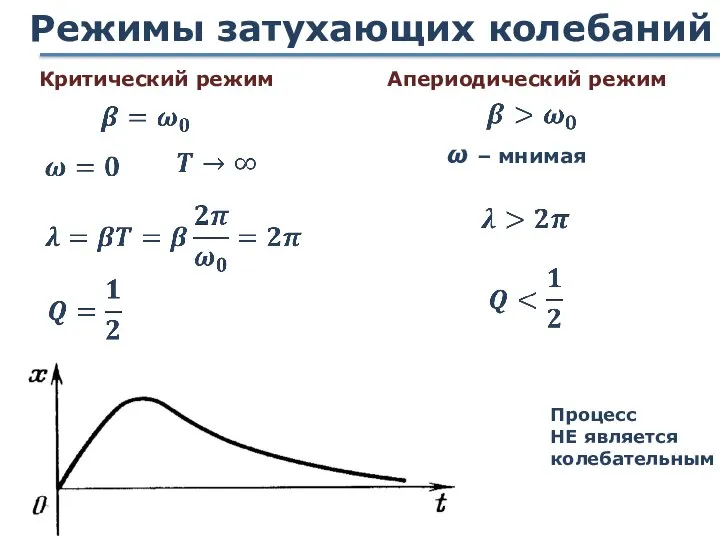
- 71. Режимы затухающих колебаний Критический режим Апериодический режим ω – мнимая Процесс НЕ является колебательным
- 72. Режимы затухающих колебаний
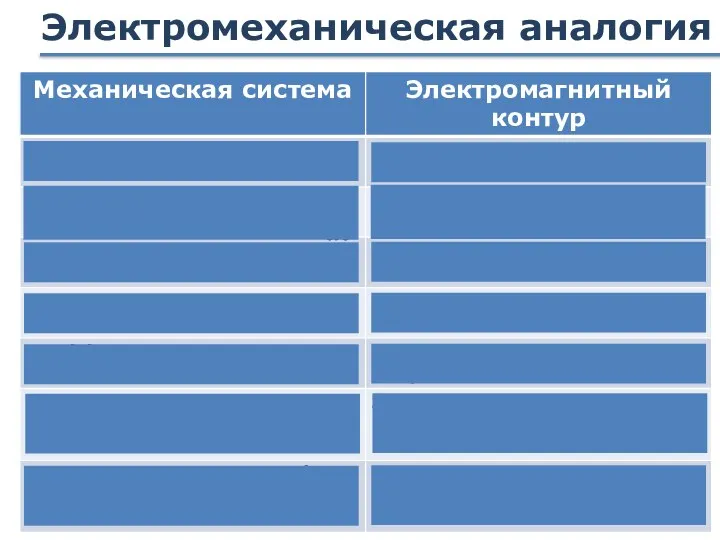
- 73. Электромеханическая аналогия
- 74. Контрольные вопросы Назовите параметры затухающих колебаний Нарисуйте зависимость амплитуды затухающих колебаний от времени
- 75. Контрольные вопросы Как изменится период колебаний маятника при увеличении массы груза в два раза? маятник пружинный
- 76. Вынужденные колебания
- 77. Вынужденные колебания Свободные колебания реальной колебательной системы всегда являются затухающими Что можно/нужно сделать, чтобы ослабить/исключить затухание?
- 78. Уравнение вынужденных колебаний По II з-ну Ньютона Разделим это уравнение на m, перенесем члены, содержащие x
- 79. Уравнение вынужденных колебаний Силы, действующие на систему Разделим это уравнение на m, перенесем члены, содержащие x
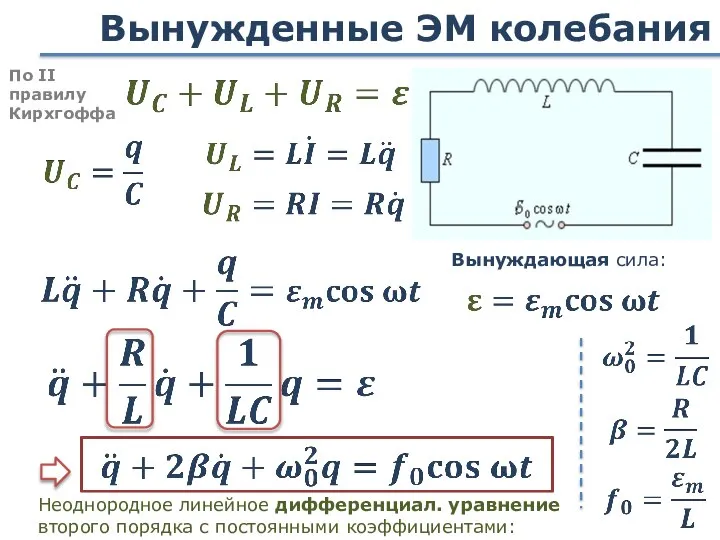
- 80. Вынужденные ЭМ колебания По II правилу Кирхгоффа Вынуждающая сила: Неоднородное линейное дифференциал. уравнение второго порядка с
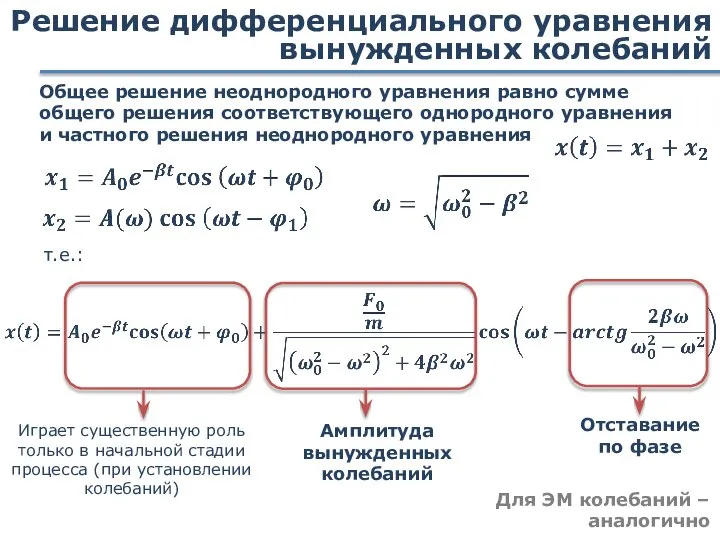
- 81. Решение дифференциального уравнения вынужденных колебаний Общее решение неоднородного уравнения равно сумме общего решения соответствующего однородного уравнения
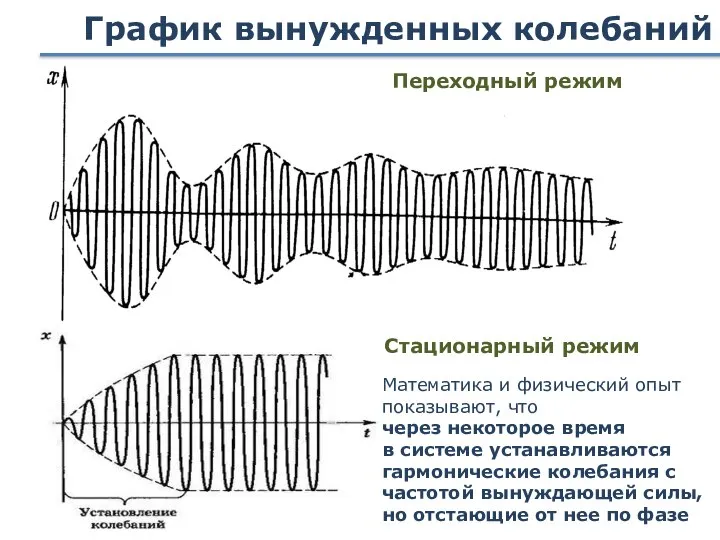
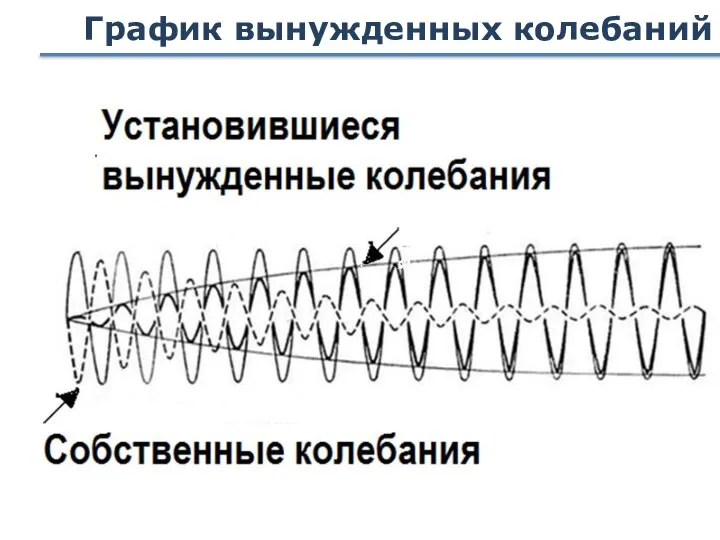
- 82. График вынужденных колебаний Стационарный режим Переходный режим Математика и физический опыт показывают, что через некоторое время
- 83. График вынужденных колебаний
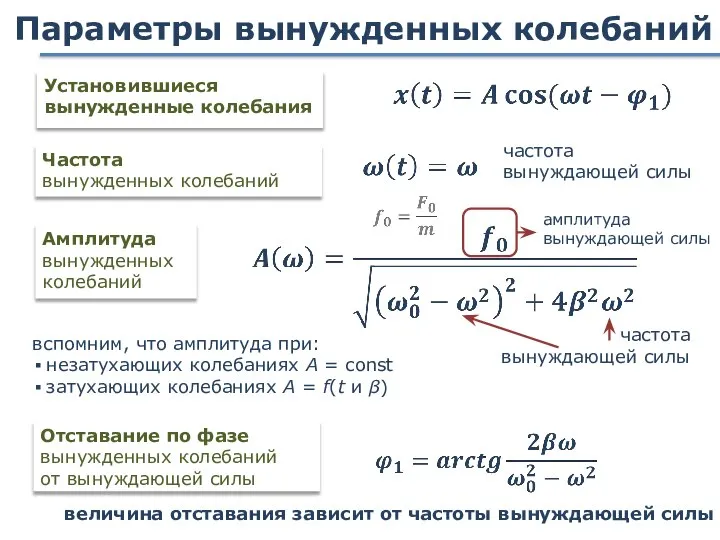
- 84. Параметры вынужденных колебаний Отставание по фазе вынужденных колебаний от вынуждающей силы Установившиеся вынужденные колебания Амплитуда вынужденных
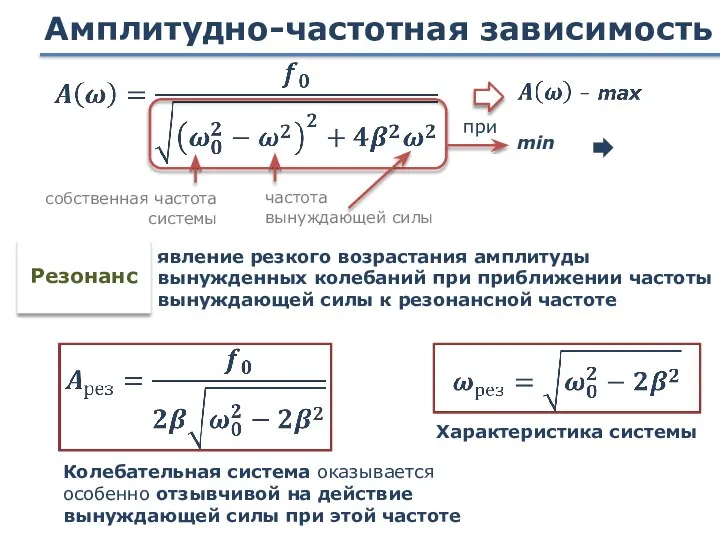
- 85. Амплитудно-частотная зависимость min явление резкого возрастания амплитуды вынужденных колебаний при приближении частоты вынуждающей силы к резонансной
- 86. Резонансная частота при ? Полученное уравнение имеет два решения: «-» не имеет физического смысла, остается со
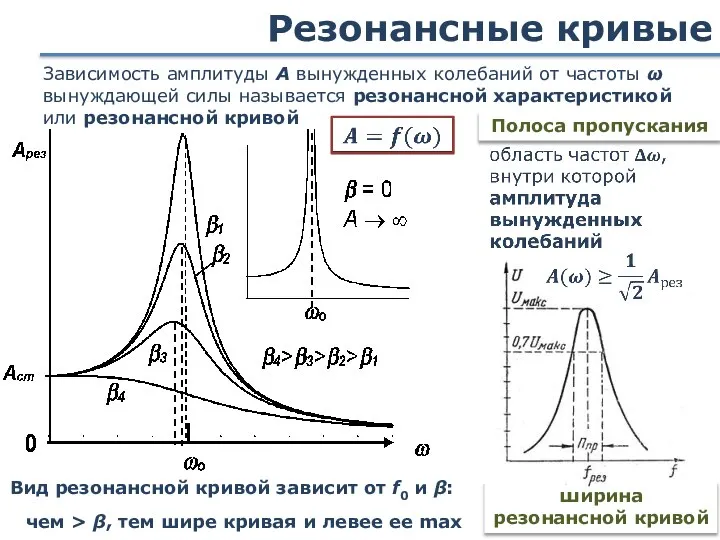
- 87. Резонансные кривые Вид резонансной кривой зависит от f0 и β: чем > β, тем шире кривая
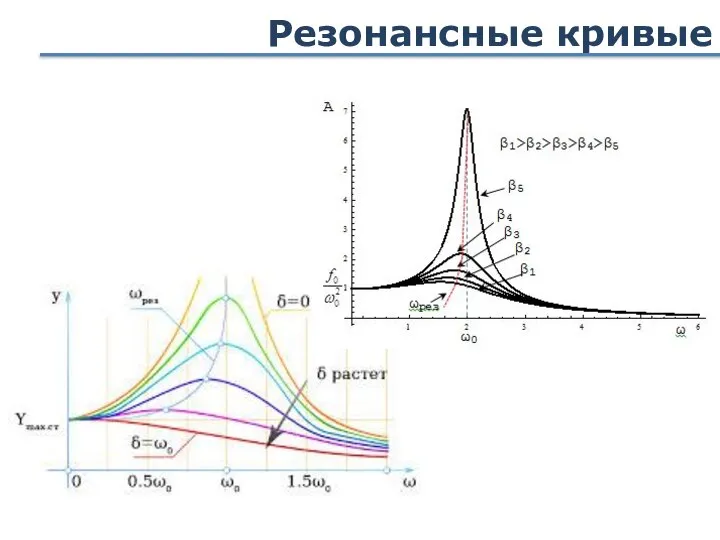
- 88. Резонансные кривые
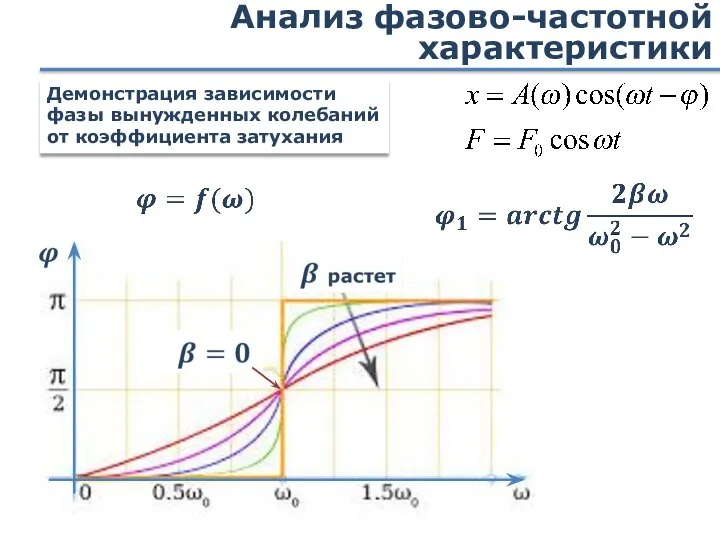
- 89. Анализ фазово-частотной характеристики Демонстрация зависимости фазы вынужденных колебаний от коэффициента затухания
- 90. Резонанс Явления резонанса играют большую роль в технике, как положительную, так и отрицательную На основе использования
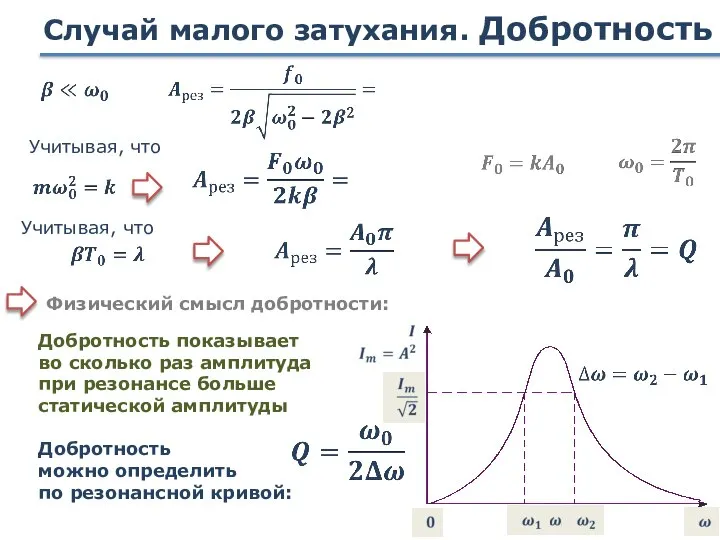
- 91. Случай малого затухания. Добротность Добротность показывает во сколько раз амплитуда при резонансе больше статической амплитуды Учитывая,
- 92. Вынужденные колебания в реальных условиях
- 93. Повторение и обобщение Дифференциальные уравнения колебаний гармонические затухающие вынужденные Решения дифференциальных уравнений колебаний гармонические затухающие вынужденные
- 94. Задача Установите соответствие между амплитудными значениями напряжений на этих элементах и амплитудным значением напряжения источника
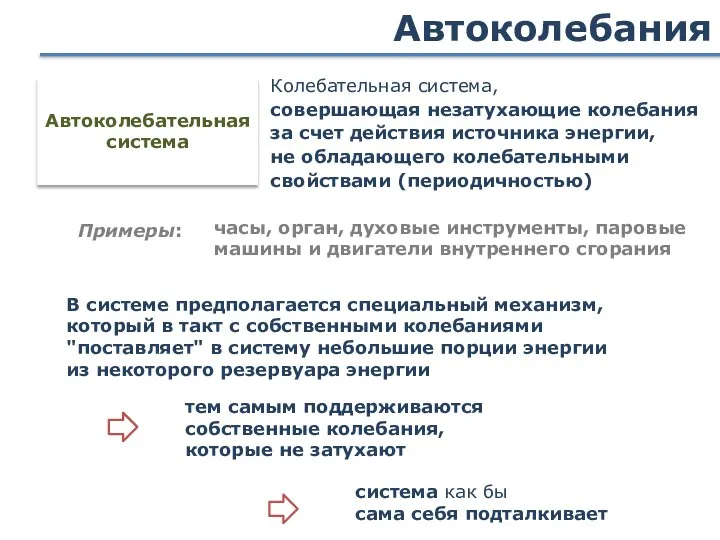
- 95. Автоколебания часы, орган, духовые инструменты, паровые машины и двигатели внутреннего сгорания Колебательная система, совершающая незатухающие колебания
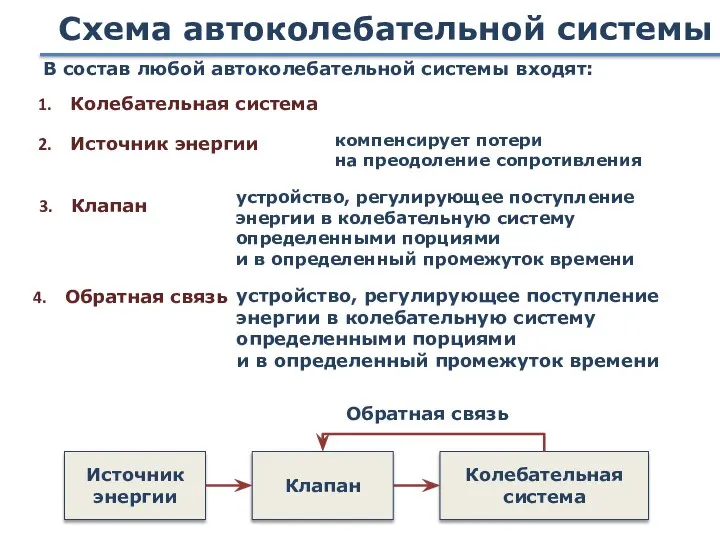
- 96. Схема автоколебательной системы Источник энергии Клапан Колебательная система Обратная связь В состав любой автоколебательной системы входят:
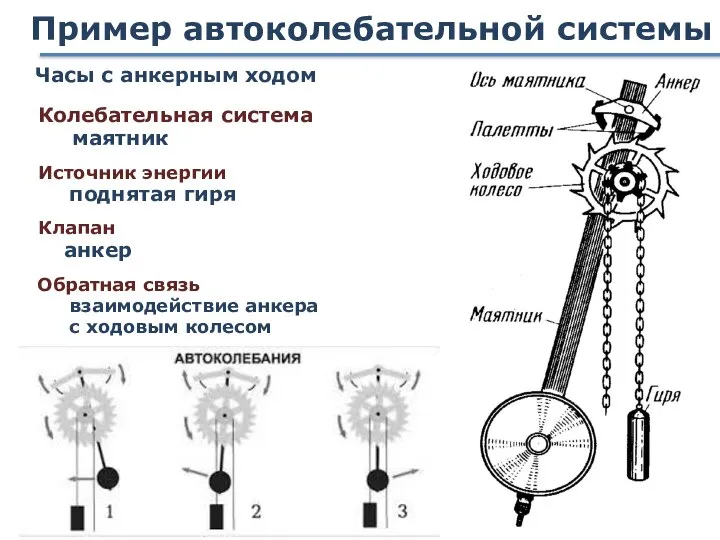
- 97. Пример автоколебательной системы Часы с анкерным ходом Колебательная система Источник энергии Клапан Обратная связь взаимодействие анкера
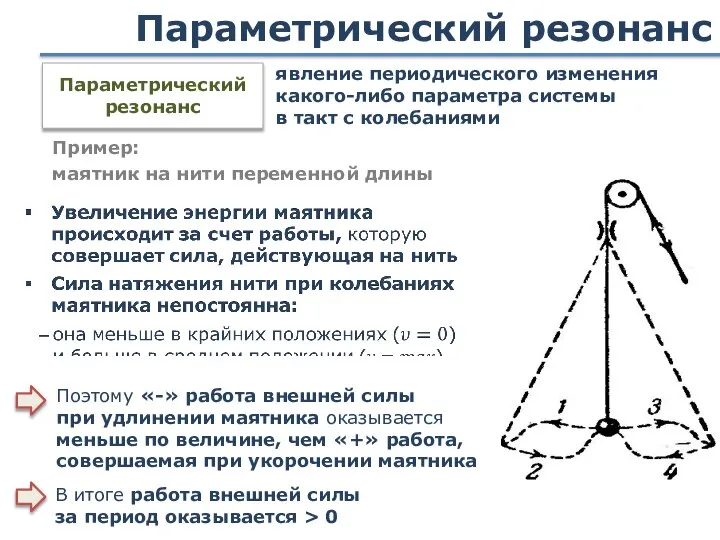
- 98. Параметрический резонанс Пример: маятник на нити переменной длины явление периодического изменения какого-либо параметра системы в такт
- 99. Контрольные вопросы и задача Дайте определение вынужденных колебаний Дайте определение резонанса Какую частоту называют резонансной? 4.
- 101. Скачать презентацию










































 Опиливание заготовок из металла и пластмассы
Опиливание заготовок из металла и пластмассы Решение задач ЕГЭ на закон Джоуля Ленца
Решение задач ЕГЭ на закон Джоуля Ленца Гидродинамика
Гидродинамика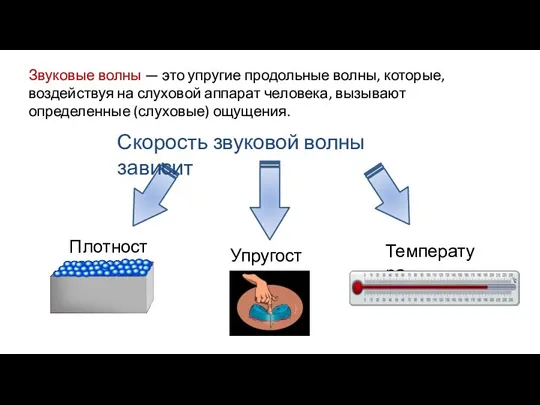 Звуковые волны
Звуковые волны Топливо будущего
Топливо будущего Школа юного исследователя
Школа юного исследователя Магнитостатическое поле в вакууме. Часть 3
Магнитостатическое поле в вакууме. Часть 3 Элементарная теория атома водорода по бору
Элементарная теория атома водорода по бору Свободное падение тел_ Движение с ускорением свободного падения
Свободное падение тел_ Движение с ускорением свободного падения Сила
Сила Динамика вращательного движения твердого тела
Динамика вращательного движения твердого тела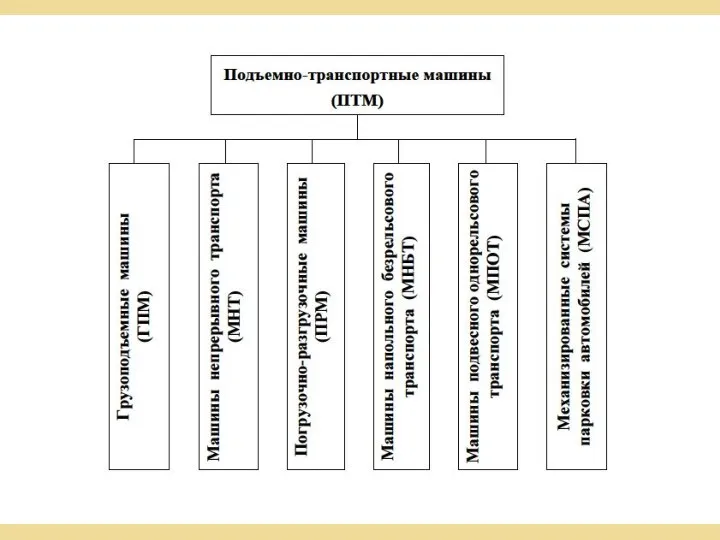 Классификация подъемно-транспортных машин
Классификация подъемно-транспортных машин Пример построения наблюдателя для системы 3-го порядка
Пример построения наблюдателя для системы 3-го порядка Презентация на тему Калейдоскоп физических явлений
Презентация на тему Калейдоскоп физических явлений  Генерирование электрической энергии. Трансформаторы. (11 класс)
Генерирование электрической энергии. Трансформаторы. (11 класс) Виды сил
Виды сил Как уменьшить силу трения
Как уменьшить силу трения Презентация на тему Дисперсия света (11 класс)
Презентация на тему Дисперсия света (11 класс) 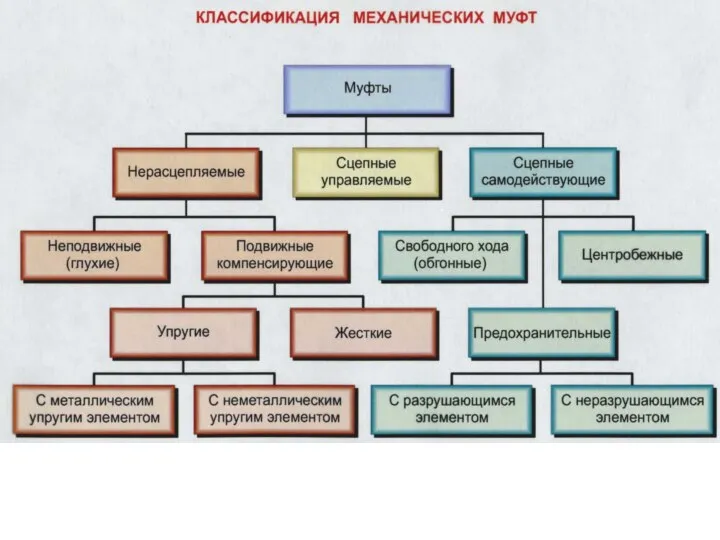 Классификация механических муфт
Классификация механических муфт Исследование изменения со временем температуры остывающей воды
Исследование изменения со временем температуры остывающей воды Радиоволны. Свойства
Радиоволны. Свойства Шредингер теңдеуін бөлшектердің стационар күйлеріне қатысты қарапайым есептеріне қолдану
Шредингер теңдеуін бөлшектердің стационар күйлеріне қатысты қарапайым есептеріне қолдану Физика атома и атомного ядра
Физика атома и атомного ядра Скорость истечения и расход жидкости для различных форм отверстий
Скорость истечения и расход жидкости для различных форм отверстий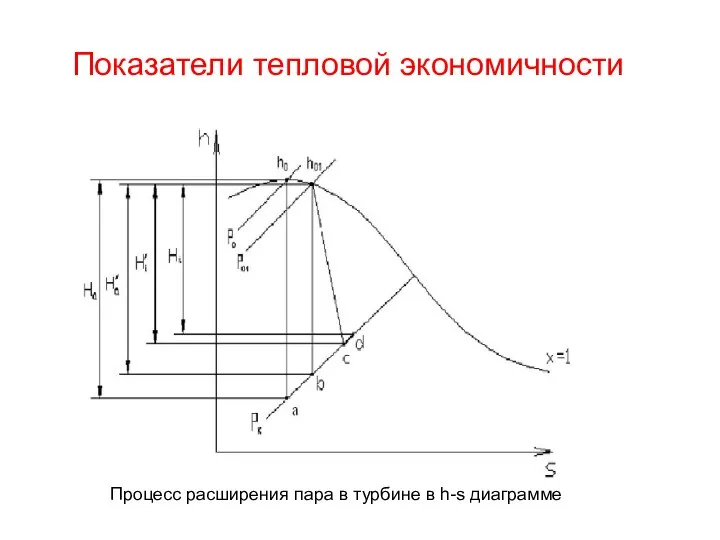 Показатели тепловой экономичности
Показатели тепловой экономичности Механическое движение (7 класс)
Механическое движение (7 класс) Классификация физико- химических методов исследования. Лекция №2
Классификация физико- химических методов исследования. Лекция №2 Открытый урок по физике в 9 классе. Явление электромагнитной индукции МОУ «СОШ №19» Г.о. Электросталь
Открытый урок по физике в 9 классе. Явление электромагнитной индукции МОУ «СОШ №19» Г.о. Электросталь