Содержание
- 2. Список литературы Савельев И.В. Курс общей физики. В 5-и тт. Том 2. Электричество и магнетизм. ISBN
- 3. Основные темы Явление электромагнитной индукции. Электродвижущая сила индукции. Методы измерения магнитной индукции. Токи Фуко. Явление самоиндукции.
- 4. Явление электромагнитной индукции В 1831 году Фарадей обнаружил, что в замкнутом проводящем контуре при изменении потока
- 5. Явление электромагнитной индукции Величина Еi не зависит от способа, которым осуществляется изменение магнитного потока Φ, и
- 6. Явление электромагнитной индукции Силу тока I1 в контуре 1 можно изменять с помощью реостата. Этот ток
- 7. Явление электромагнитной индукции Индукционный ток I2 можно вызвать также, приближая контур 2 к контуру 1 или
- 8. Явление электромагнитной индукции Ленц установил правило, позволяющее найти направление индукционного тока. Правило Ленца гласит, что индукционный
- 9. Явление электромагнитной индукции При удалении контура 2 от контура 1 возникает ток I’’2, момент которого p’’m
- 10. Электродвижущая сила индукции Итак, мы выяснили, что изменение магнитного потока Φ через контур вызывает возникновение в
- 11. Электродвижущая сила индукции Приведем перемычку в движение со скоростью v. С той же скоростью станут перемещаться
- 12. Электродвижущая сила индукции Действие этой силы эквивалентно действию на электрон электрического поля напряженности Это поле неэлектростатического
- 13. Электродвижущая сила индукции Будем считать Еi положительной в том случае, когда ее направление образует с направлением
- 14. Электродвижущая сила индукции Осуществим в полученном выражении циклическую перестановку, после умножим и разделим на dt. Из
- 15. Электродвижущая сила индукции Таким образом, приходим к выражению Как видим знаки в правой и левой частях
- 16. Электродвижущая сила индукции Единицей потока магнитной индукции в СИ служит вебер (Вб), который представляет собой поток
- 17. Электродвижущая сила индукции В случае, если геометрия контура постоянна, а магнитный поток изменяется за счет изменения
- 18. Электродвижущая сила индукции Если контур, в котором индуцируется ЭДС, состоит не из одного витка, а из
- 19. Методы измерения магнитной индукции Пусть полный магнитный поток, сцепленный с некоторым контуром, изменяется от значения Ψ1
- 20. Методы измерения магнитной индукции Проинтегрировав это выражение, найдем, полный заряд: Соотношение (8.10) лежит в основе разработанного
- 21. Методы измерения магнитной индукции Тогда полный магнитный поток, сцепленный с катушкой , будет равен Где S
- 22. Методы измерения магнитной индукции Следовательно, изменение полного потока при повороте катушки равно Ψ1-Ψ2=2NBS Если поворот катушки
- 23. Методы измерения магнитной индукции Измерив q и зная R, N и S, можно по формуле (8.11)
- 24. Методы измерения магнитной индукции Еще один вариант – использовать свойство висмута, у которого сопротивление сильно возрастает
- 25. Токи Фуко Индукционные токи могут возбуждаться и в сплошных массивных проводниках. В этом случае их называют
- 26. Токи Фуко Поэтому движущиеся в сильном магнитном поле хорошие проводники испытывают сильное торможение, обусловленное взаимодействием токов
- 27. Токи Фуко Торможение возникает лишь при движении пластины и исчезает, когда пластина неподвижна. Поэтому электромагнитный успокоитель
- 28. Токи Фуко Таким способом осуществляют плавление металлов в вакууме, что позволяет получать материалы высокой чистоты. Бытовые
- 29. Токи Фуко Токи Фуко, возникающие в проводах, по которым текут переменные токи, направлены так, что ослабляют
- 30. Явление самоиндукции Электрический ток, текущий в любом контуре, создает пронизывающий этот контур магнитный поток Ψ. При
- 31. Явление самоиндукции Коэффициент пропорциональности L между силой тока и полным магнитным потоком называется индуктивностью контура. Линейная
- 32. Явление самоиндукции Кроме того, при неизменной силе тока I полный поток может изменяться за счет изменения
- 33. Явление самоиндукции В гауссовой системе индуктивность имеет размерность длины. В соответствии с этим единицу индуктивности в
- 34. Явление самоиндукции Поток через каждый из витков равен Φ=BS, а полный магнитный поток, сцепленный с соленоидом,
- 35. Явление самоиндукции При изменениях силы тока в контуре возникает ЭДС самоиндукции ES, равная Если при изменениях
- 36. Явление самоиндукции В данном случае причиной, вызывающей ES является изменение силы тока в цепи. Примем в
- 37. Явление самоиндукции Производная dI/dt положительна в двух случаях: либо при возрастании положительного тока, либо при убывании
- 38. Явление самоиндукции Соотношение (8.16) дает возможность определить индуктивность L как коэффициент пропорциональность между скоростью изменения силы
- 39. Ток при замыкании и размыкании цепи По правилу Ленца дополнительные токи, возникающие вследствие самоиндукции, всегда направлены
- 40. Ток при замыкании и размыкании цепи Сопротивление источника будем считать пренебрежительно малым. В момент времени t=0
- 41. Ток при замыкании и размыкании цепи Преобразуем выражение (8.19) до вида И продифференцируем полученное выражение, в
- 42. Ток при замыкании и размыкании цепи Найдем значение const из начальных условий. При t=0 сила тока
- 43. Ток при замыкании и размыкании цепи Величину τ называют постоянной времени цепи. Подставим в формулу (8.22)
- 44. Ток при замыкании и размыкании цепи Для упрощения расчетов мы считали, что цепь в момент отключения
- 45. Ток при замыкании и размыкании цепи Уравнение (8.24) является линейным неоднородным дифференциальным уравнением. В соответствии с
- 46. Взаимная индукция Возьмем два контура 1 и 2, расположенных близко друг к другу. Если в контуре
- 47. Взаимная индукция Аналогично при протекании в контуре 2 тока силы I2 возникает сцепленный с контуром 1
- 48. Взаимная индукция Коэффициенты пропорциональности L12 и L21 называются взаимной индуктивностью контуров. Расчеты показывают, что при отсутствии
- 49. Взаимная индукция Найдем взаимную индуктивность двух катушек, намотанных на общий тороидальный железный сердечник. Линии магнитной индукции
- 50. Взаимная индукция Магнитный поток через поперечное сечение сердечника равен Φ=BS=μ0μHS, где S – площадь поперечного сечения
- 51. Взаимная индукция Однако в данном случае нельзя утверждать, что L12=L21. Множитель μ, входящий в выражения для
- 52. Энергия магнитного поля Рассмотрим цепь, изображенную на рисунке. При замкнутом ключе в соленоиде установится ток I,
- 53. Энергия магнитного поля Если индуктивность соленоида не зависит от I (L=const), то dΨ=LdI и выражение (8.34)
- 54. Энергия магнитного поля Совершение этой работы сопровождается исчезновением магнитного поля, которое первоначально существовало в окружающем соленоид
- 55. Энергия магнитного поля Эта энергия (8.37) локализована в возбуждаемом током магнитном поле. Сравним эту формулу с
- 56. Энергия магнитного поля Проделав такие же преобразования, что привели нас к (8.35), получим выражение, совпадающее с
- 57. Энергия магнитного поля Выразим энергию магнитного поля (8.37) через величины, характеризующие само поле. В случае очень
- 58. Энергия магнитного поля Следовательно энергия (8.39) локализована внутри соленоида и распределена по объему с постоянной плотностью
- 59. Энергия магнитного поля Зная плотность энергии поля в каждой точке, можно вычислить энергию поля, заключенного в
- 60. Работа перемагничивания ферромагнетика При отсутствии ферромагнетиков работа (8.38) полностью идет на создание магнитного поля. При наличии
- 62. Скачать презентацию



























































 Развитие познавательного интереса к предмету физика
Развитие познавательного интереса к предмету физика Законы Кирхгофа
Законы Кирхгофа Проверка знаний по теме Ядерный реактор
Проверка знаний по теме Ядерный реактор Открытия на большом адронном коллайдере
Открытия на большом адронном коллайдере Все загадки света. Оптика
Все загадки света. Оптика Определение электромагнитного поля. Практическое занятие
Определение электромагнитного поля. Практическое занятие Проект СТО для легковых и грузовых автомобилей на трассе Нур-Султан – Караганда
Проект СТО для легковых и грузовых автомобилей на трассе Нур-Султан – Караганда Презентация на тему Двигатель внутреннего сгорания: принципы
Презентация на тему Двигатель внутреннего сгорания: принципы  Вопросы к госэкзамену
Вопросы к госэкзамену Детали машин. Основные положения (тема 3.1)
Детали машин. Основные положения (тема 3.1) Физика для одноклассников. Индивидуальный проект
Физика для одноклассников. Индивидуальный проект Голография и ее применение
Голография и ее применение Внутренняя энергия. Теплопередача. Работа в термодинамике
Внутренняя энергия. Теплопередача. Работа в термодинамике Изучаем фотоэффект
Изучаем фотоэффект Лазер. Лазерное излучение
Лазер. Лазерное излучение Задачи для курсовой работы
Задачи для курсовой работы Физика. Тест 1-15
Физика. Тест 1-15 Свободные и вынужденные электромагнитные колебания
Свободные и вынужденные электромагнитные колебания Аттестационная работа. Дозиметр
Аттестационная работа. Дозиметр Полупроводниковые приборы
Полупроводниковые приборы Частотные методы синтеза
Частотные методы синтеза Импульс тела. Закон сохранения импульса
Импульс тела. Закон сохранения импульса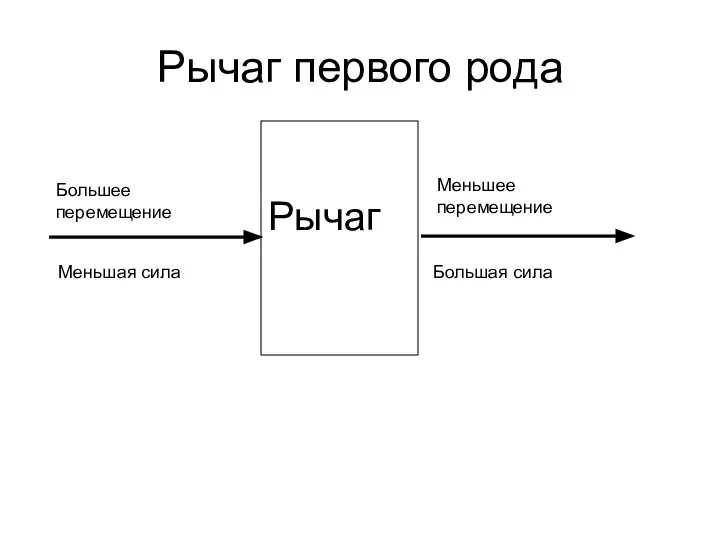 Рычаг первого рода
Рычаг первого рода Основы технической механики
Основы технической механики Трение - полезное или вредное явление?
Трение - полезное или вредное явление? Дисперсия света. Опыт И. Ньютона
Дисперсия света. Опыт И. Ньютона Идеальный газ в молекулярно-кинетической теории. Среднее значение квадрата скорости молекул
Идеальный газ в молекулярно-кинетической теории. Среднее значение квадрата скорости молекул Инструменты, механизмы и технические устройства
Инструменты, механизмы и технические устройства