Слайд 2Интерференция света
Интерференция — одно из наиболее убедительных доказательств волновых свойств.
Интерференция присуща волнам

любой природы.
Интерференцией световых волн называется сложение двух когерентных волн, вследствие которого наблюдается усиление или ослабление результирующих световых колебаний в различных точках пространства.
Слайд 3Когерентные волны
Для образования устойчивой интерференционной картины необходимо, чтобы источники волн были когерентными.
Волны,

имеющие одинаковую частоту и постоянную во времени разность фаз, называются когерентными.
Все источники света, кроме лазеров, некогерентные.
Слайд 4Как можно наблюдать интерференцию света?
Чтобы наблюдать интерференцию света, надо получить когерентные световые

пучки.
Для этого, до появления лазеров, во всех приборах для наблюдения интерференции света когерентные пучки получались путем разделения и последующего сведения световых лучей, исходящих из одного источника света.
Для этого использовались щели, зеркала и призмы.
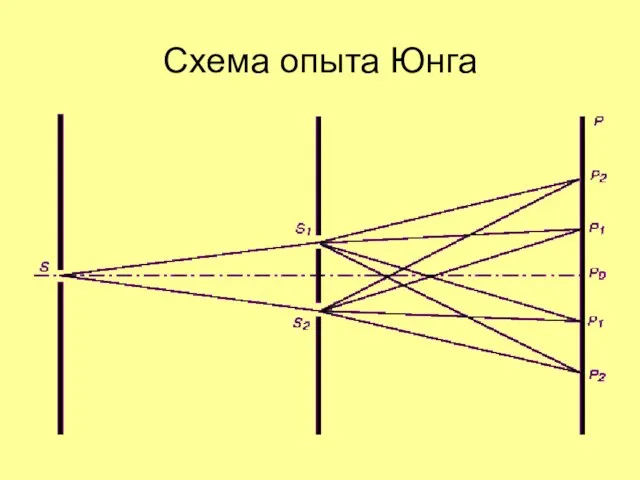
Слайд 5Опыт Юнга
В начале 19-го века английский ученый Томас Юнг поставил опыт, в

котором можно было наблюдать явление интерференции света.
Свет, пропущенный через узкую щель, падал на две близко расположенные щели, за которыми находился экран.
На экране вместо ожидаемых двух светлых полос появлялись чередующиеся цветные полосы.
Слайд 7Наблюдение интерференции в лабораторных условиях
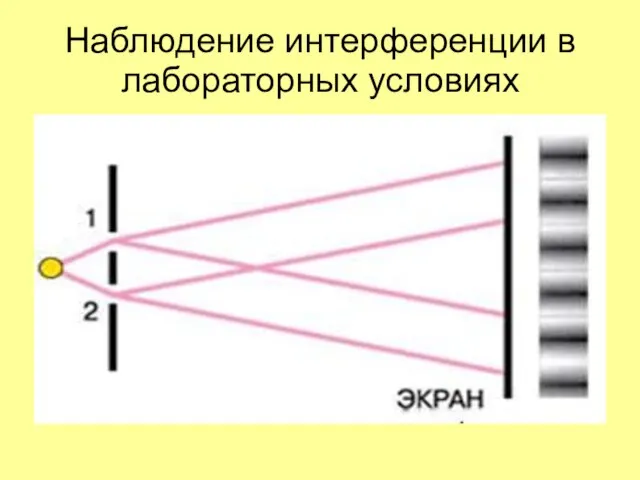
Слайд 8Интерференционные максимумы
Интерференционные максимумы наблюдаются в точках, для которых разность хода волн

∆d равна четному числу полуволн, или, что то же самое, целому числу волн:
Слайд 9Интерференционные минимумы
Интерференционные минимумы наблюдаются в точках, для которых разность хода волн ∆d

равна нечетному числу полуволн:
Слайд 10Интерференция в тонких пленках
Мы много раз наблюдали интерференционную картину, когда наблюдали за

мыльными пузырями, за радужным переливом цветов тонкой пленки керосина или нефти на поверхности воды.
Слайд 11Объяснение интерференции в тонких пленках
Происходит сложение волн, одна из которых отражается от
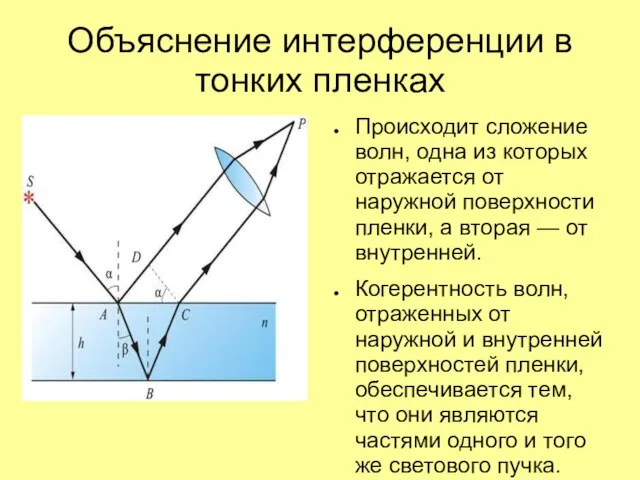
наружной поверхности пленки, а вторая — от внутренней.
Когерентность волн, отраженных от наружной и внутренней поверхностей пленки, обеспечивается тем, что они являются частями одного и того же светового пучка.
Слайд 12Объяснение цвета тонких пленок
Томас Юнг объяснил, что различие в цвете связано с

различием в длине волны (или частоте световых волн).
Световым пучкам различного цвета соответствуют волны различной длины.
Слайд 13Объяснение цвета тонких пленок
Для взаимного усиления волн, отличающихся друг от друга длиной
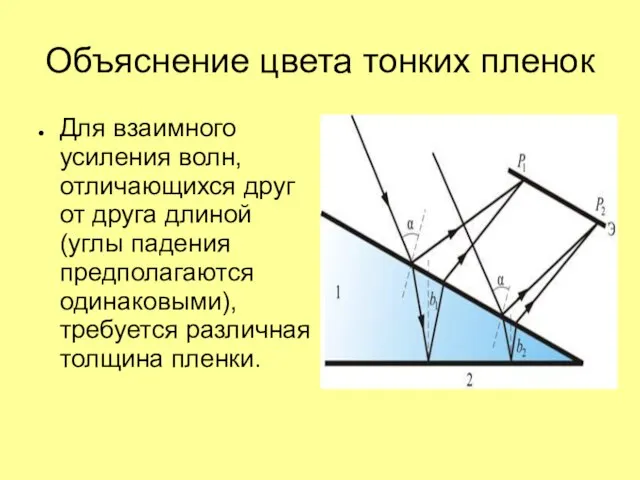
(углы падения предполагаются одинаковыми), требуется различная толщина пленки.
Слайд 14Следовательно, если пленка имеет неодинаковую толщину, то при освещении ее белым светом

должны появиться различные цвета.
Слайд 15Кольца Ньютона
Простая интерференционная картина возникает в тонкой прослойке воздуха между стеклянной пластиной
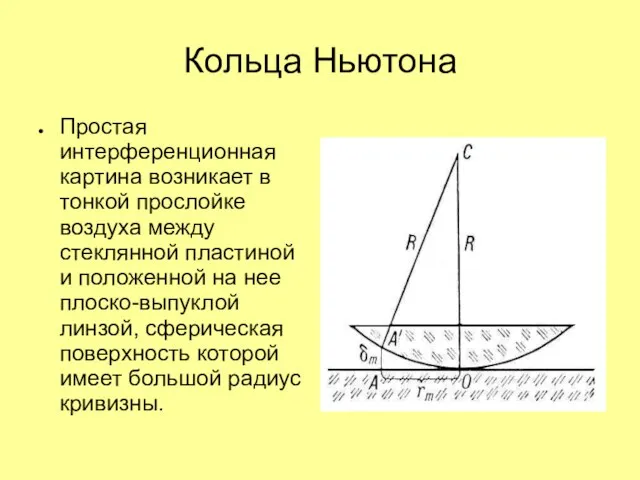
и положенной на нее плоско-выпуклой линзой, сферическая поверхность которой имеет большой радиус кривизны.
Слайд 16Интерференционная картина имеет вид концентрических колец

Слайд 17Объяснение «колец Ньютона»
Волна 1 отражается от нижней поверхности линзы, а волна 2
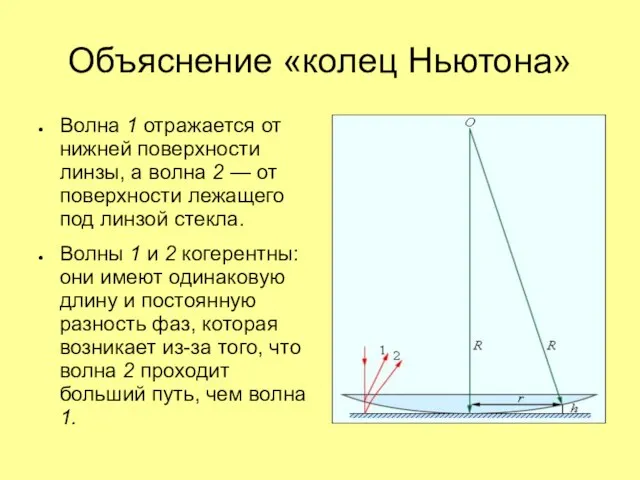
— от поверхности лежащего под линзой стекла.
Волны 1 и 2 когерентны: они имеют одинаковую длину и постоянную разность фаз, которая возникает из-за того, что волна 2 проходит больший путь, чем волна 1.
Слайд 18Определение радиуса колец Ньютона
Если известен радиус кривизны R поверхности линзы, то можно

вычислить, на каких расстояниях от точки соприкосновения линзы со стеклянной пластиной разности хода таковы, что волны определенной длины λ гасят друг друга.
Эти расстояния являются радиусами темных колец Ньютона, так как линии постоянной толщины воздушной прослойки представляют собой окружности.
Слайд 19Определение длины волны
Зная радиусы колец, можно вычислить длину волны, используя формулу
где R

— радиус кривизны выпуклой поверхности линзы (k = 0,1,2,...), r — радиус кольца.
Слайд 20Дифракция света
Дифракция света — отклонение волны от прямолинейного распространения при прохождении через
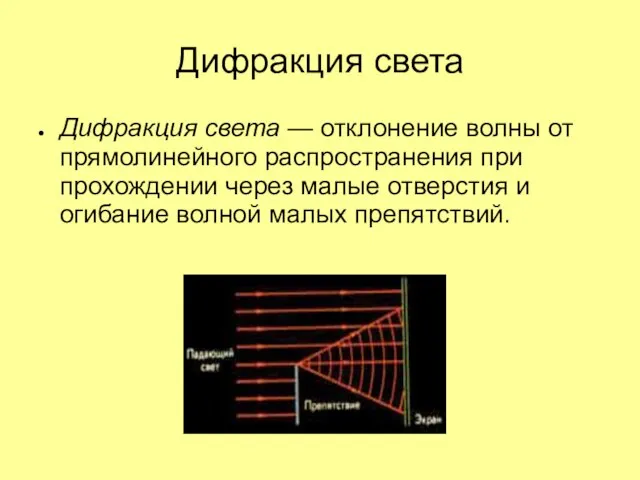
малые отверстия и огибание волной малых препятствий.
Слайд 21Условие проявления дифракции:
где d — характерный размер отверстия или препятствия, L —

расстояние от отверстия или препятствия до экрана.
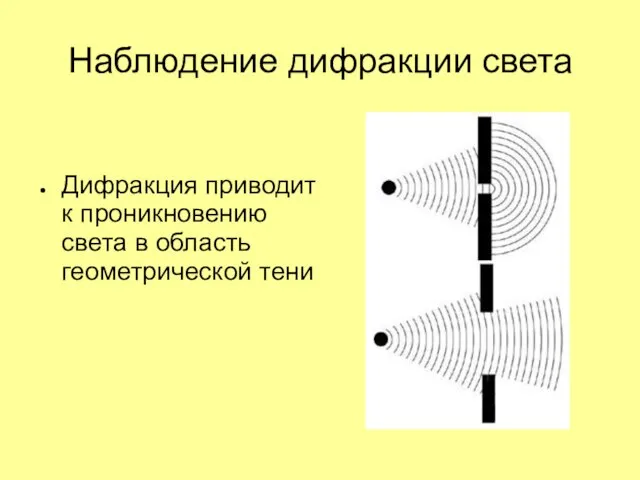
Слайд 22Наблюдение дифракции света
Дифракция приводит к проникновению света в область геометрической тени
Слайд 23Соотношение между волновой и геометрической оптикой
Одно из основных понятий волновой теории —

фронт волны.
Фронт волны — это совокупность точек пространства, до которых в данный момент дошла волна.
Слайд 24Принцип Гюйгенса
Каждая точка среды, до которой доходит волна, служит источником вторичных волн,
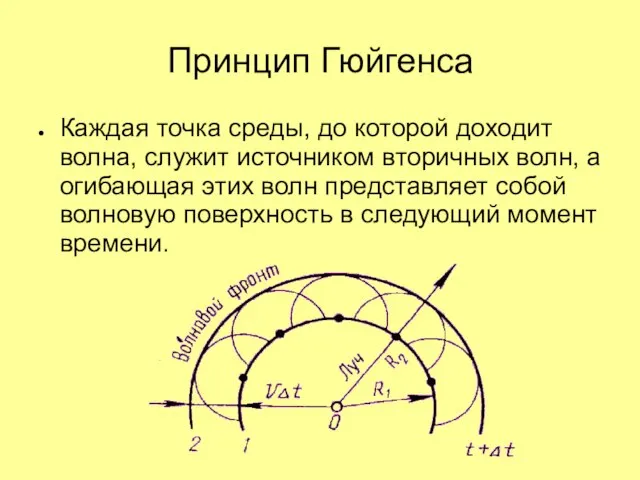
а огибающая этих волн представляет собой волновую поверхность в следующий момент времени.
Слайд 25Объяснение законов отражения и преломления света с точки зрения волновой теории
Пусть плоская

волна падает под углом на границу раздела двух сред.
Согласно принципу Гюйгенса, каждая точка этой границы сама становится источником сферических волн.
Волны, идущие во вторую среду, формируют преломленную плоскую волну.
Волны, возвращающиеся в первую среду, формируют отраженную плоскую волну.
Слайд 26Отражение света
Фронт отраженной волны BD образует такой же угол с плоскостью раздела
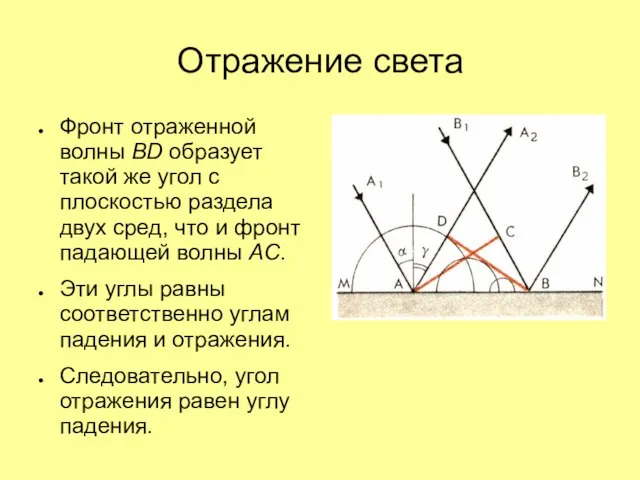
двух сред, что и фронт падающей волны AC.
Эти углы равны соответственно углам падения и отражения.
Следовательно, угол отражения равен углу падения.
Слайд 27Преломление света
Фронт падающей волны AC составляет больший угол с поверхностью раздела сред,
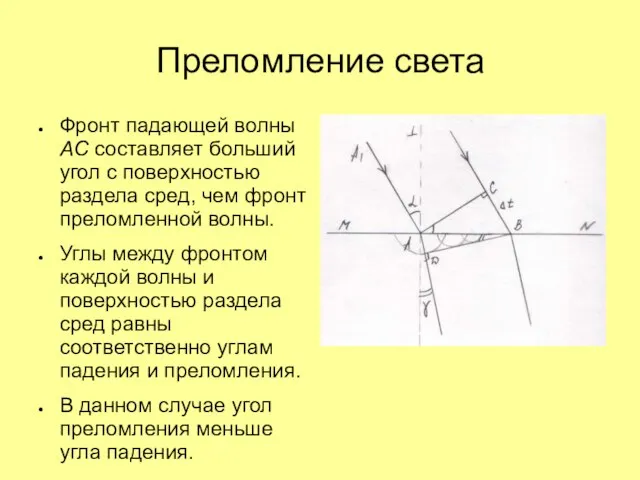
чем фронт преломленной волны.
Углы между фронтом каждой волны и поверхностью раздела сред равны соответственно углам падения и преломления.
В данном случае угол преломления меньше угла падения.
Слайд 28Закон преломления света
Расчеты показывают, что отношение синусов этих углов равно отношению скорости

света в первой среде к скорости света во второй среде.
Для данных двух сред это отношение постоянно.
Отсюда следует закон преломления: отношение синуса угла падения к синусу угла преломления постоянно для данных двух сред.
Слайд 29Физический смысл показателя преломления
Абсолютный показатель преломления равен отношению скорости света c в

вакууме к скорости света v в данной среде:



























 Установки и оборудование для аэроакустического эксперимента в ЦАГИ
Установки и оборудование для аэроакустического эксперимента в ЦАГИ Механические свойства твердых тел
Механические свойства твердых тел Перенос теплоты
Перенос теплоты Очистка загрязненной поваренной соли. Практическая работа №2
Очистка загрязненной поваренной соли. Практическая работа №2 Игровая встреча. Великие физики
Игровая встреча. Великие физики Физические явления. Наблюдения и опыт
Физические явления. Наблюдения и опыт Презентация на тему Электризация тел
Презентация на тему Электризация тел  Амплитуда колебания
Амплитуда колебания Указание по аварийной разблокировке с помощью торцевого ключа
Указание по аварийной разблокировке с помощью торцевого ключа Statika
Statika Электростатика. Заря́д
Электростатика. Заря́д Физика Космоса
Физика Космоса Своя игра. 7 класс
Своя игра. 7 класс Кинематика точки
Кинематика точки Механическое движение. Повторение
Механическое движение. Повторение Презентация на тему Вклад отечественной физики в Великую Победу
Презентация на тему Вклад отечественной физики в Великую Победу  Механические колебания
Механические колебания Структурный анализ и синтез механизмов. Лекция 2
Структурный анализ и синтез механизмов. Лекция 2 Сила
Сила Магнитные явления
Магнитные явления Генерирование электрической энергии. Трансформаторы. (11 класс)
Генерирование электрической энергии. Трансформаторы. (11 класс) Электрическое поле. Делимость электрического заряда. Электрон. Строение атомов
Электрическое поле. Делимость электрического заряда. Электрон. Строение атомов Испарение и конденсант
Испарение и конденсант Физика – это наука о природе!
Физика – это наука о природе! Презентация на тему Электромагнитные колебания и волны
Презентация на тему Электромагнитные колебания и волны  ВКР Ремонт ходовой части и системы рулевого управления УАЗ 3163
ВКР Ремонт ходовой части и системы рулевого управления УАЗ 3163 Модель атома Резерфорда
Модель атома Резерфорда Зрение домашних животных
Зрение домашних животных