Содержание
- 2. Лекция 8 Квантово-механические методы вычисления эффективных сечений взаимодействий Теория возмущений. Упругое рассеяние электронов. Первое приближение теории
- 3. Теория возмущений В волновой механике задача вычисления эффективных сечений взаимодействия частиц друг с другом решается при
- 4. Рассмотрим взаимодействие электрона с атомом, в этом случае имеем: Пусть до взаимодействия атом находится в начальном
- 5. После взаимодействия атом переходит в другое n′ состояние и изменяется энергия электрона. Новое значение энергии электрона
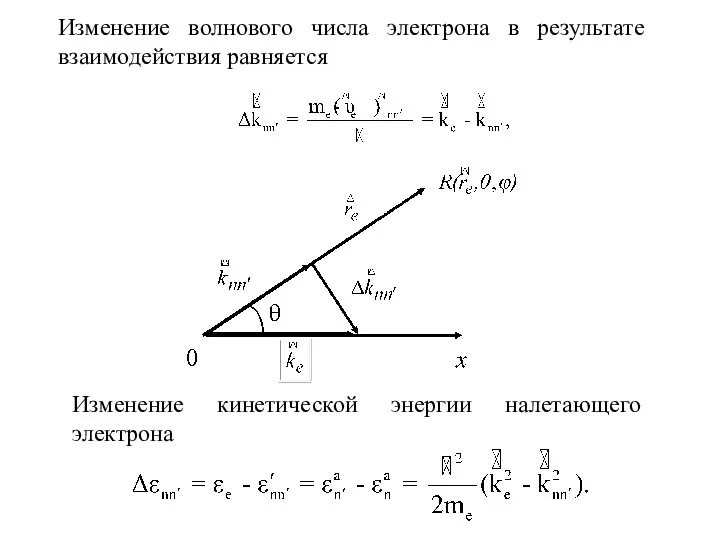
- 6. Изменение кинетической энергии налетающего электрона Изменение волнового числа электрона в результате взаимодействия равняется
- 7. Обозначим волновую функцию упруго рассеянных электронов через Обозначим волновую функцию неупруго рассеянных электронов через должна представлять
- 8. первичного потока налетающих частиц параллельно OX и характеризуемого плоской волной и потока упруго рассеянных частиц, выражаемого
- 9. частиц, вызвавших переход частицы-мишени из начального n состояния в конечное n′ состояние и находящихся вблизи точки
- 10. то плотность потока налетающих электронов равна Поэтому в первичной волне при условии Ne=1 плотность потока налетающих
- 11. По определению дифференциальное эффективное сечение рассеяния на единичный телесный угол численно равняется отношению потока рассеянных в
- 12. Выведенная формула определяет понятие дифференциального эффективного сечения рассеяния частиц в единичный телесный угол с точки зрения
- 13. Для вычисления амплитуды рассеяния составляется волновое уравнение системы атом - налетающий электрон в виде Здесь:
- 14. Физически каждый член этой суммы соответствует совокупности атома, перешедшего из n в n′ состояние, и электрона,
- 15. Одним из них является первое приближение теории возмущений (first order perturbation theory), обычно называемое методом Борна,
- 16. соответствующее отсутствию взаимодействия, дает решение задачи в первом борновском приближении. В таком приближении, когда силы, действующие
- 17. Дальнейший анализ требует раскрытия вида функции П(r). Чтобы вычислить этот матричный элемент, необходимо задаться определенным законом
- 18. где Z - заряд ядра,
- 19. Далее, после стандартных преобразований, получим выражение для вычисления дифференциального эффективного сечения рассеяния электронов на атомах в
- 20. Упругое рассеяние электронов При упругом взаимодействии частиц их квантовые состояния не меняются, n=n′, тогда δnn=1. Также
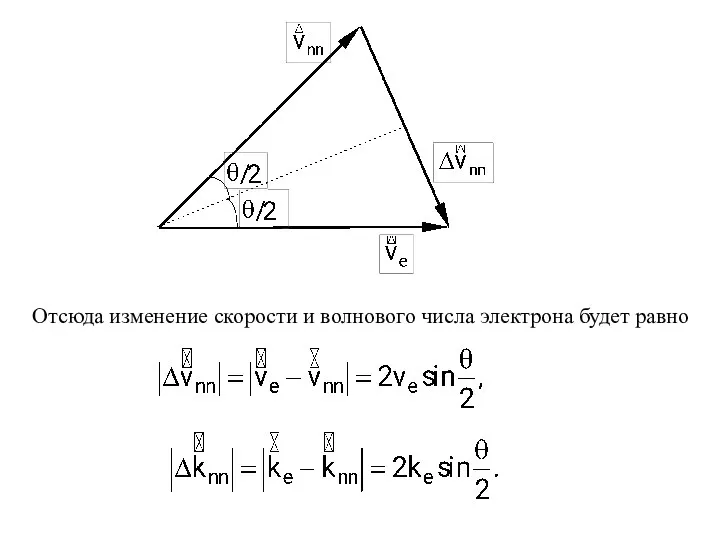
- 21. Отсюда изменение скорости и волнового числа электрона будет равно
- 23. В простейших случаях, соответствующих распределению заряда в атомах водорода и гелия в основных состояниях и без
- 24. Исследуем это выражение для различных конкретных условий соударений. 1) Это означает, что скорость налетающего электрона во
- 25. Если и углы рассеяния θ не очень малы (на языке классической физики - не очень большие
- 26. 2) Для случая рассеяния на малые углы, т.е. при больших прицельных расстояниях формула Резерфорда дает в
- 27. 3) Рассеяние на большие углы, т.е. Для этих условий Так как мы решаем задачу в борновском
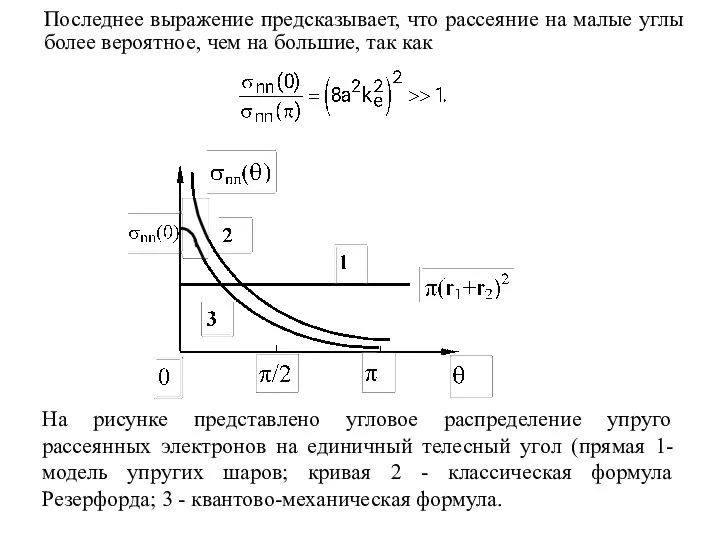
- 28. Последнее выражение предсказывает, что рассеяние на малые углы более вероятное, чем на большие, так как На
- 29. 4) Это условие означает малые скорости налетающих электронов. Этот случай выходит за пределы применимости борновского приближения.
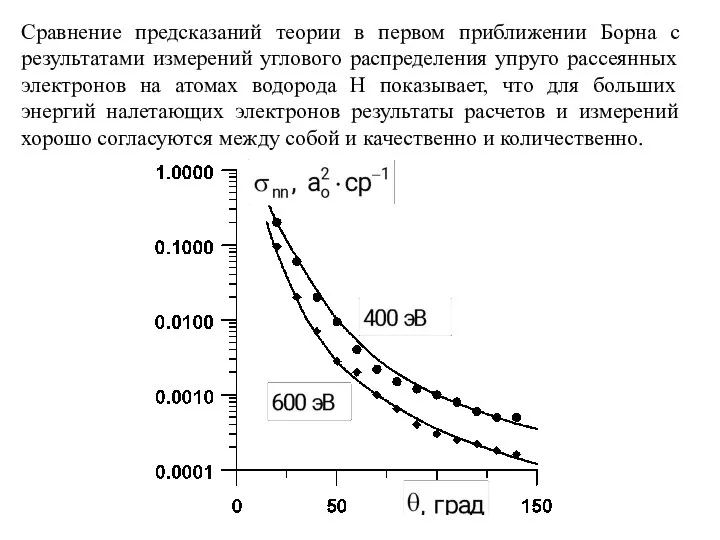
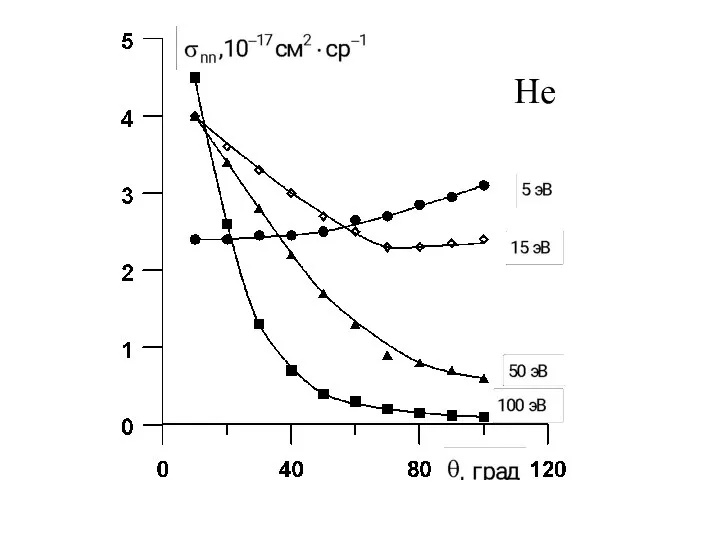
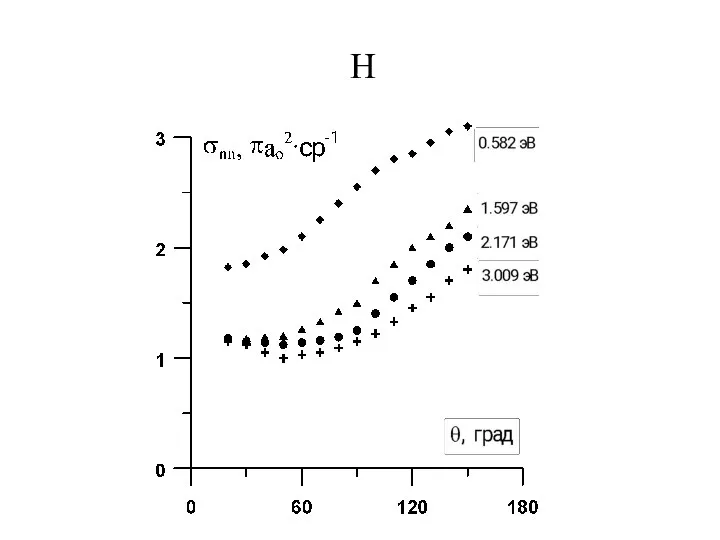
- 30. Сравнение предсказаний теории в первом приближении Борна с результатами измерений углового распределения упруго рассеянных электронов на
- 31. He
- 32. H
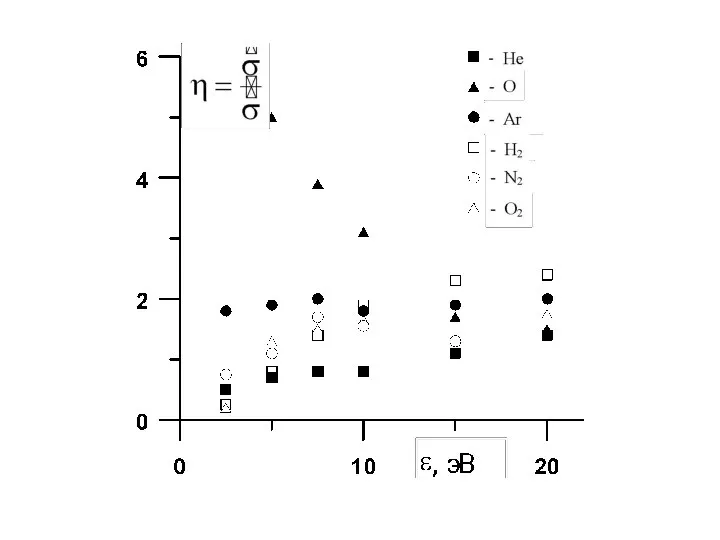
- 34. Значение полного эффективного сечения упругого рассеяния электронов атомами и молекулами получается после интегрирования дифференциального эффективного сечения
- 35. Возбуждение энергетических уровней и ионизация атомов и молекул электронным ударом n≠n′, δnn′=0 Атомный фактор в выражении
- 36. То есть вероятность возбуждения перехода n→n′ с рассеянием электронов на малые углы пропорциональна квадрату дипольного момента
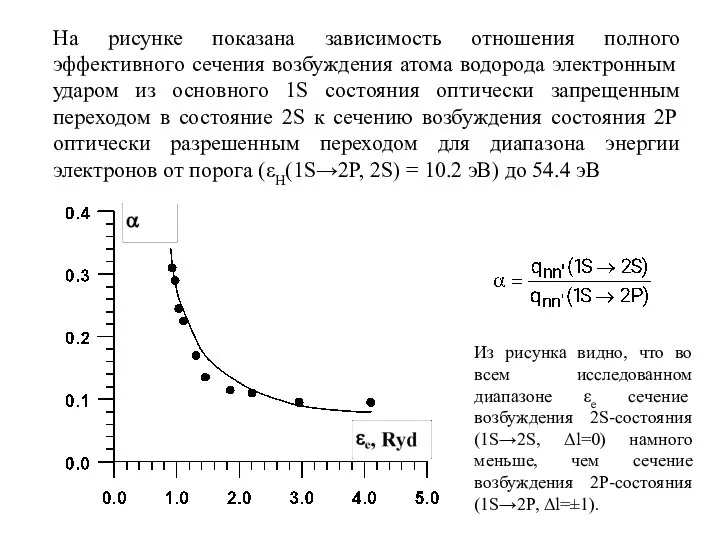
- 37. На рисунке показана зависимость отношения полного эффективного сечения возбуждения атома водорода электронным ударом из основного 1S
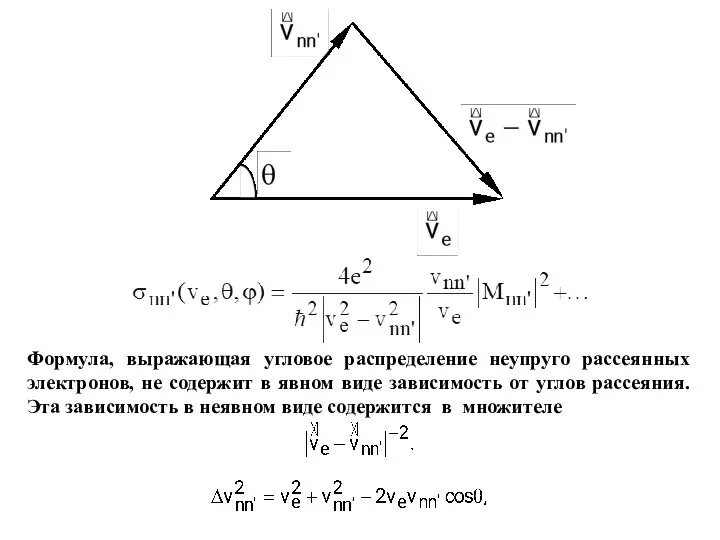
- 38. Формула, выражающая угловое распределение неупруго рассеянных электронов, не содержит в явном виде зависимость от углов рассеяния.
- 39. Проинтегрировав дифференциальное эффективное сечение рассеяния в единичный телесный угол по Δk, найдем полное сечение возбуждения атома
- 64. Скачать презентацию




















































 Исследовательская работа по физике Модель двигателя Стирлинга
Исследовательская работа по физике Модель двигателя Стирлинга Теория относительности. Релятивистская механика
Теория относительности. Релятивистская механика Презентация на тему Источники электрического тока
Презентация на тему Источники электрического тока  Индукция магнитного поля
Индукция магнитного поля Геометрическое движение в физике
Геометрическое движение в физике Техническое обслуживание масляного выключателя ВМП-10к
Техническое обслуживание масляного выключателя ВМП-10к Физика атомного ядра
Физика атомного ядра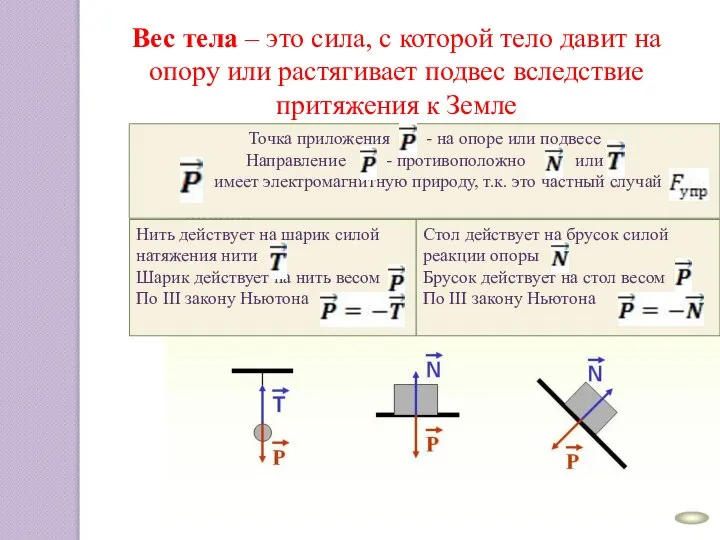 Вес тела
Вес тела Основное урвнение МКТ идеального газа
Основное урвнение МКТ идеального газа Газовые законы. Решение задач на газовые законы. 10 класс
Газовые законы. Решение задач на газовые законы. 10 класс Телескоп. Рефрактор
Телескоп. Рефрактор Переменный электрический ток
Переменный электрический ток Лекція 2 Динаміка матеріальної точки
Лекція 2 Динаміка матеріальної точки Третий закон Ньютона
Третий закон Ньютона Основные положения молекулярно-кинетической теории. 10 класс. Тест
Основные положения молекулярно-кинетической теории. 10 класс. Тест Выпуск первого автомобиля в г. Тольятти
Выпуск первого автомобиля в г. Тольятти Виды излучений
Виды излучений Плоские электромагнитные волны
Плоские электромагнитные волны Действие магнитного поля на проводник с током
Действие магнитного поля на проводник с током Криволинейное движение. Равномерное движение материальной точки по окружности. Линейная и угловая скорости
Криволинейное движение. Равномерное движение материальной точки по окружности. Линейная и угловая скорости Консультация по физике
Консультация по физике Спектральный анализ
Спектральный анализ Презентация на тему Полупроводники
Презентация на тему Полупроводники  Связь ДПФ и ДВПФ
Связь ДПФ и ДВПФ Механические явления. 7 класс
Механические явления. 7 класс Механическое движение. Решение задач
Механическое движение. Решение задач mypresentation.ru
mypresentation.ru Тренажер формул по физике Постоянный электрический ток
Тренажер формул по физике Постоянный электрический ток