Элементы релятивистской механики (продолжение). Лекция № 9

Преобразования Лоренца
Преобразования Лоренца при переходе от K- к K΄-СО (Лекция № 8, ф-ла (8.5а)):
где

При обратном переходе от K΄- к K-системе отсчета (Лекция № 8, ф-ла (8.5б)):

Кинематические следствия из преобразований Лоренца
Сокращение длин отрезков, параллельных
относительно неподвижного наблюдателя
Замедление часов: В точке с координатой x΄ K΄-СО протекает процесс, длительность которого в этой системе
(собственное время процесса). Длительность этого процесса в K- системе, относительно которой K΄-система движется

проекции которой υx, υy и υz. В K΄-СО
Релятивистский закон сложения скоростей
В K-системе движется частица со скоростью

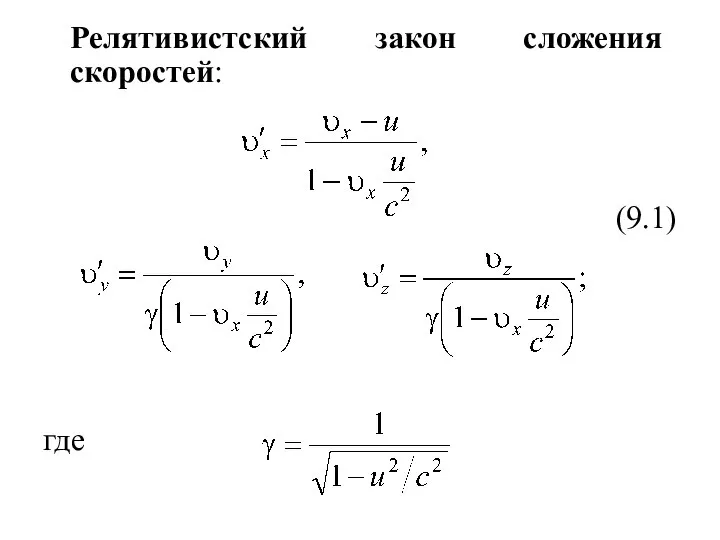
Релятивистский закон сложения скоростей:
(9.1)
где

Аналогично находим обратные зависимости, для вычисления скорости в K-СО, если она известна в K΄-СО:
(9.2)

Интервал
В релятивистской механике физический процесс – это последовательность событий.
Понятие события включает место, где оно произошло (его координаты x, y, z) и момент времени t, когда оно произошло.
Интервал между двумя событиями (S12 ):
t12 – промежуток времени между событиями, l12 – расстояние между точками 1 и 2, в которых происходят данные события.

Во всех ИСО интервал между событиями 1 и 2 одинаков:
Типы интервалов:
1) пространственноподобный
2) времениподобный
3) светоподобный

Для (1) – пространственноподобного интервала всегда можно найти такую K΄-систему в которой оба события происходят одновременно (t΄12 = 0):
Для (2) – времениподобного интервала всегда можно найти такую K΄-СО, в к-рой оба события происходят в одной точке (l΄12 = 0):

Существуют причинно связанные и причинно не связанные события.
В случае пространственноподобных интервалов (l12 > ct12) ни в одной СО события не могут оказать влияния друг на друга, даже если связь между событиями осуществлялась со скоростью c = 3·108 м/с .
Такие события не причинно-связаны (сигнал не может дойти).
События, разделенные времениподобными и светоподобными интервалами (l12 ≤ ct12) могут быть причинно-связанными друг с другом, т.к. сигнал может дойти из т. 1 в т. 2 со скоростью с.

Элементы релятивистской динамики
Релятивистская масса частицы
(9.3)
m0 – масса (покоя) частицы, υ – скорость движения частицы.
Релятивистский импульс
(9.4)

Основное уравнение релятивистской динамики
частицы в ИСО при любых возможных скоростях υ < c
(9.5)

Как и в ньютоновской механике, приращение кинетической энергии частицы под действием силы
ЗАКОН ВЗАИМОСВЯЗИ МАССЫ И ЭНЕРГИИ
Кинетическая энергия релятивистской частицы

Согласно (9.5)
где
Упростим это выражение, используя (9.3):

Возведем (9.3) в квадрат
Найдем дифференциал этого выражения, учитывая, что m0 и c – постоянные:

Если разделить это равенство на 2m, то его правая часть совпадет с выражением для dEk
(9.6)
Кинетическая энергия покоящейся частицы равна нулю, а ее релятивистская масса
Кинетическая энергия частицы, движущейся со скоростью υ:
(9.7)

Перепишем (9.7) в форме:
(9.8)
Здесь
(9.9)
– энергия покоя частицы (это общая внутренняя энергия тела),
(9.10)
– полная энергия частицы.
(9.11)

Связь между импульсом и энергией релятивистской частицы
Полная энергия ε и импульс p частицы имеют разные значения в разных СО.
Однако существует некоторая комбинация ε и p, которая является инвариантной т.е. имеет одно и то же значение в разных СО:
(9.12)
Убедимся в правильности (9.12) подставив в неё (9.10) и