Энергия. Работа. Законы сохранения. Лекция 5

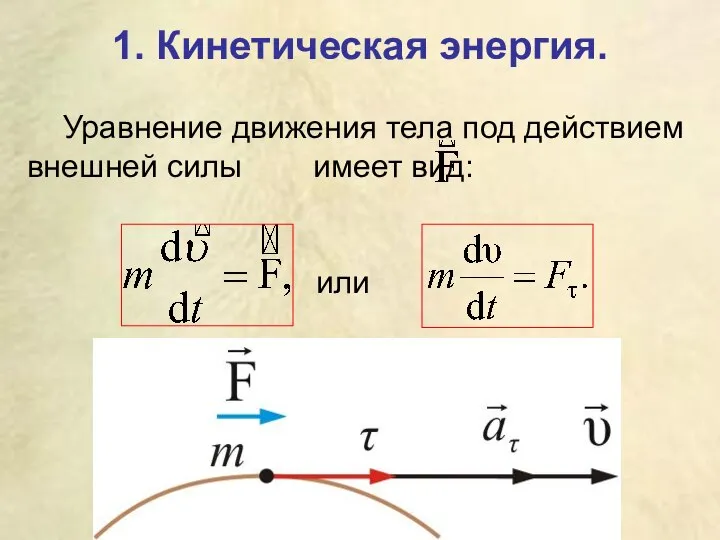
1. Кинетическая энергия.
Уравнение движения тела под действием внешней силы имеет вид:
или

Умножим обе части этого равенства на
получим:
Левая часть равенства, есть полный дифференциал некоторой функции:
или

Т.о.
Если система замкнута, то и
тогда и
Если полный дифференциал некоторой функции, описывающей поведение системы равен нулю, то эта функция может служить характеристикой состояния данной системы.

Функция состояния системы, определяемая только скоростью ее движения, называется кинетической энергией.
Кинетическая энергия системы есть функция состояния движения этой системы.
K – аддитивная величина:

Энергия измеряется в СИ в единицах произведения силы на расстояние, т.е. в ньютонах на метр:
Кроме того, в качестве единицы измерения энергии используется внесистемная единица – электрон-вольт (эВ): 1 эВ = 1,6 1019 Дж.

отсюда
Связь кинетической энергии с импульсом p.
Т.к.

Связь кинетической энергии с работой.
Если постоянная сила действует на тело, то оно будет двигаться в направлении силы. Тогда, элементарная работа по перемещению тела из т. 1 в т. 2, будет равна произведению силы F на перемещение dr :

отсюда
Т.к. нам известно, что
а тогда после замены получим выражение для работы:
Окончательно получаем:

Следовательно, работа силы приложенной к телу на пути r численно равна изменению кинетической энергии этого тела:
Или изменение кинетической энергии dK равно работе внешних сил:
Работа, так же как и кинетическая энергия, измеряется в джоулях.

Мощность есть работа, совершаемая в единицу времени.
Мгновенная мощность
или
Средняя мощность
Измеряется мощность в ваттах. 1 Вт = 1 Дж/с.
Скорость совершения работы (передачи энергии) называется мощность.

2. Консервативные силы и системы
Кроме контактных взаимодействий, наблюдаются взаимодействия между телами, удаленными друг от друга. Подобное взаимодействие осуществляется посредством физических полей (особая форма материи).
Каждое тело создает вокруг себя поле, которое проявляет себя именно воздействием на другие тела.

Силы, работа которых не зависит от пути, по которому двигалось тело, а зависит от начального и конечного положения тела называются консервативными.
Обозначим A – работа консервативных сил, по перемещению тела из т. 1 в т. 2

Изменение направления движения на противоположное – вызывает изменение знака работы консервативных сил. Отсюда следует, что работа консервативных сил вдоль замкнутой кривой равна нулю:
Интеграл по замкнутому контуру L,
– называется циркуляцией вектора

Если циркуляция какого-либо вектора силы равна нулю, то эта сила консервативна.
Консервативные силы: сила тяжести, электростатические силы, силы центрального стационарного поля.
Неконсервативные силы: силы трения, силы вихревого электрического поля.
Консервативная система – такая, внутренние силы которой только консервативные, внешние – консервативны и стационарны.

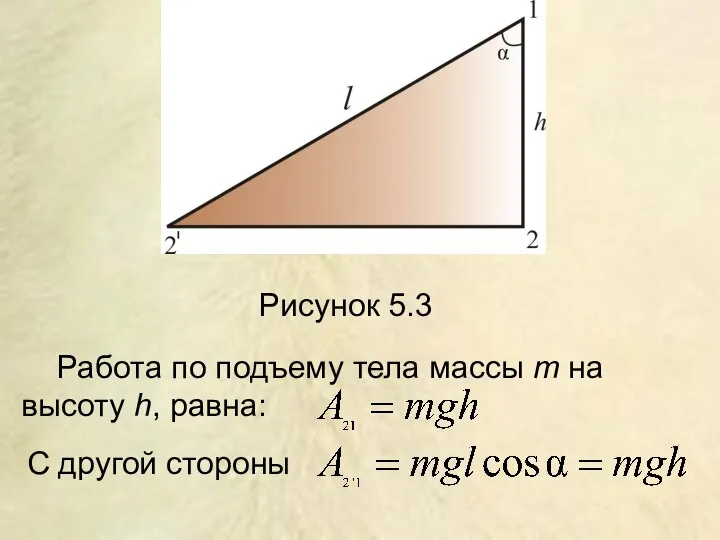
Рисунок 5.3
Работа по подъему тела массы m на высоту h, равна:
С другой стороны

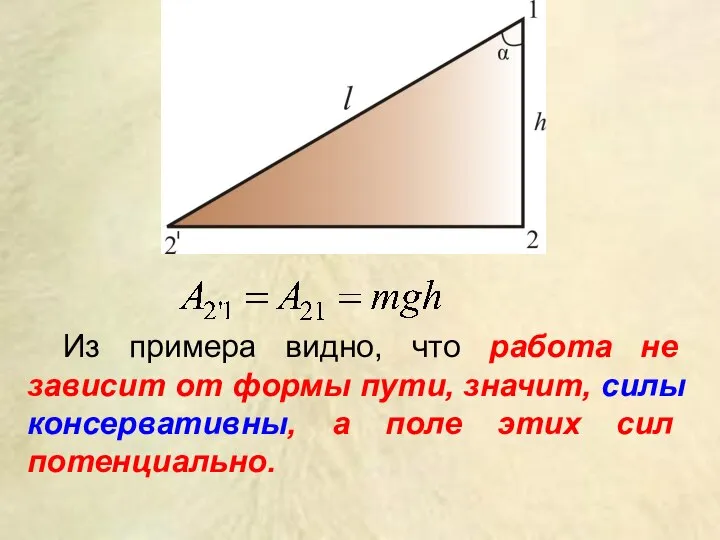
Из примера видно, что работа не зависит от формы пути, значит, силы консервативны, а поле этих сил потенциально.

3. Потенциальная энергия
Если на систему материальных тел действуют консервативные силы, то можно ввести понятие потенциальной энергии.
Работа, совершаемая консервативными силами при изменении конфигурации системы, не зависит от того как было осуществлено это изменение. Работа определяется только начальной и конечной конфигурациями системы:

Потенциальная энергия U (х, у, z) – функция состояния системы, зависящая только от координат всех тел системы в поле консервативных сил.
K – определяется скоростью движения тел системы, а U – их взаимным расположением.
Работа консервативных сил равна убыли потенциальной энергии:

Потенциальная энергия при гравитационном взаимодействии
Работа тела при падении
Или
Условились считать, что на поверхности земли
тогда т.е.

Потенциальная энергия упругой деформации (пружины)
Найдём работу, совершаемую при деформации упругой пружины.
Сила упругости Сила непостоянна, поэтому элементарная работа
знак минус говорит о том, что работа совершенна над пружиной.

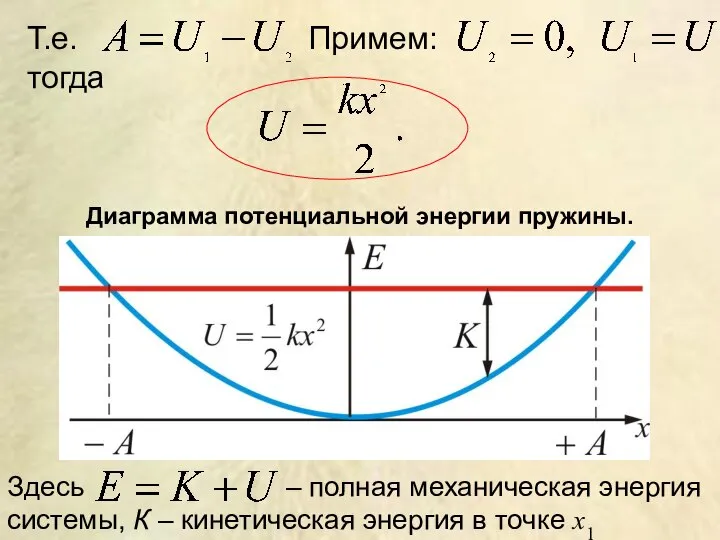
Т.е. Примем:
тогда
Диаграмма потенциальной энергии пружины.
Здесь – полная механическая энергия системы, К – кинетическая энергия в точке x1

4. Закон сохранения механической энергии
Закон сохранения сводит воедино результаты, полученные нами раньше.
В сороковых годах девятнадцатого века трудами Р. Майера, Г. Гельмгольца и Дж. Джоуля (все в разное время и независимо друг от друга) был доказан закон сохранения и превращения энергии.

Первые уроки по физике ему давал Дж. Дальтон, под влиянием которого Джоуль начал свои эксперименты. Работы посвящены механике, электромагнетизму, кинетической теории газов.
Джоуль Джеймс Прескотт (1818 –1889) – английский физик, один из первооткрывателей закона сохранения энергии.

Рассмотрим систему, состоящую из N-частиц.
Силы взаимодействия между частицами
- консервативные.
Кроме внутренних сил на частицы действуют внешние консервативные и неконсервативные силы, т. е. рассматриваемая система частиц или тел консервативна.

Для консервативной системы частиц можно найти полную энергию системы:
Для механической энергии закон сохранения звучит так: полная механическая энергия консер-вативной системы материальных точек остаётся постоянной.

Для замкнутой системы, т.е. для системы на которую не действуют внешние силы, можно записать:
т.е. полная механическая энергия замкнутой системы материальных точек, между которыми действуют только консервативные силы, остаётся постоянной.

Если в замкнутой системе действуют неконсервативные силы, то полная механическая энергия системы не сохраняется – частично она переходит в другие виды энергии – неконсервативные.
Система, в которой механическая энергия переходит в другие виды энергии, называется диссипативной, сам процесс перехода называется диссипацией энергии.

6. Применение законов сохранения
6.1. Абсолютно упругий центральный удар
При абсолютно неупругом ударе закон сохранения механической энергии не работает.
Применим закон сохранения механической энергии для расчета скорости тел при абсолютно упругом ударе – это такой удар, при котором не происходит превращения механической энергии в другие виды энергии.

Удар частиц
Ударом точечных частиц называется такое механическое взаимодействие при непосредственном контакте и за бесконечно малое время при котором частицы обмениваются энергией и импульсом при условии, что система частиц остается замкнутой
Различают два вида ударов абсолютно неупругий удар
такой удар, при котором после удара частицы движутся как единое целое и абсолютно упругий удар удар, при котором после удара частицы движутся с различными скоростями и в течении удара выполняются законы сохранения (энергии и импульса)
Абсолютно упругий удар бывает двух типов
- нецентральный удар
- центральный удар

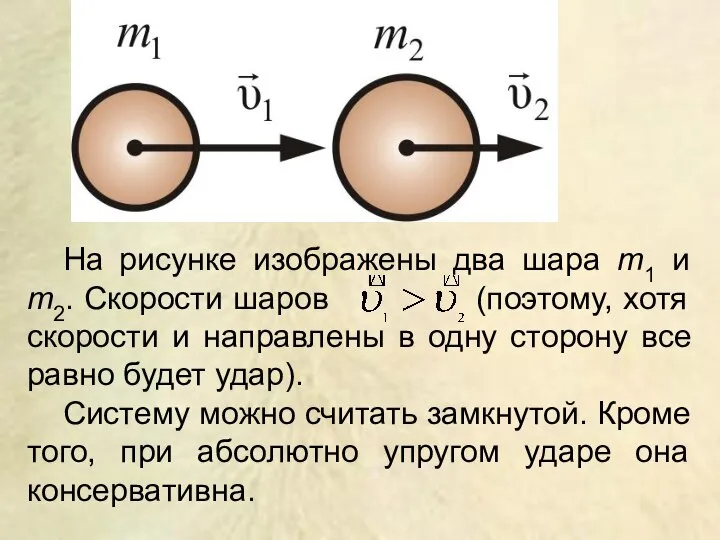
На рисунке изображены два шара m1 и m2. Скорости шаров (поэтому, хотя скорости и направлены в одну сторону все равно будет удар).
Систему можно считать замкнутой. Кроме того, при абсолютно упругом ударе она консервативна.

Обозначим и – скорости шаров после их столкновения.
В данном случае можно воспользоваться законом сохранения механической энергии и законом сохранения импульса (в проекциях на ось x):
По ЗСЭ
По ЗСИ

Решив эту систему уравнений относительно
и получим
Таким образом, скорости шаров после абсолютно упругого удара не могут быть одинаковыми по величине и по направлению.

Рассмотрим теперь абсолютно упругий удар шара о неподвижную массивную стенку.
Стенку можно рассматривать как неподвижный шар с массой
Разделим числитель и знаменатель на m2 и пренебрежем тогда
т.е.

Таким образом, шар изменит скорость на противоположную.
Т.к. , то получим

6.2. Абсолютно неупругий удар
Абсолютно неупругий удар – это столкновение двух тел, в результате которого тела объединяются и двигаются дальше, как единое целое.
Продемонстрировать абсолютно неупругий удар можно с помощью шаров из пластилина (глины), движущихся навстречу друг другу.

Если массы шаров m1 и m2, их скорости до удара то используя закон сохранения импульса, можно записать
где – скорость движения шаров после удара. Тогда:

Если шары двигались навстречу друг другу, то они вместе будут продолжать двигаться в ту сторону, в которую двигался шар, обладающий большим импульсом. В частном случае, если массы и скорости шаров равны, то
Выясним, как меняется кинетическая энергия шаров при центральном абсолютно неупругом ударе.

Так как в процессе соударения шаров между ними действуют силы, зависящие не от самих деформаций, а от их скоростей, то мы имеем дело с силами, подобными силам трения, поэтому закон сохранения механической энергии не должен соблюдаться. Вследствие деформации происходит «потеря» кинетической энергии, перешедшей в тепловую или другие формы энергии (диссипация энергии). Эту «потерю» можно определить по разности кинетических энергий до и после удара:

Отсюда, получаем
Если ударяемое тело было первоначально неподвижно то

Когда (масса неподвижного тела очень большая), то и почти вся кинетическая энергия при ударе переходит в другие формы энергии. Поэтому, например, для получения значительной деформации наковальня должна быть массивнее молотка.
Когда
тогда и практически вся энергия затрачивается на возможно большее перемещение, а не на остаточную деформацию (например, молоток – гвоздь).