Содержание
- 2. INTRODUCTION So far covered: Ohm’s law and Kirchhoff’s laws This lecture covers powerful techniques for circuit
- 3. Nodal Analysis In nodal analysis, we are interested in finding the node voltages by applying KCL
- 4. Example Calculate the node voltages in the circuit shown The fact that i2 is negative shows
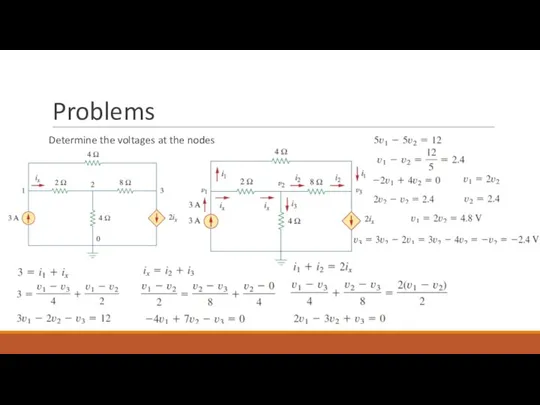
- 5. Problems Determine the voltages at the nodes
- 6. Problems Determine the voltages at the nodes
- 7. Nodal Analysis with Voltage Sources CASE 1: If a voltage source is connected between the reference
- 8. Example For the circuit shown find the node voltages.
- 9. Problems Find v and i in the circuit
- 10. Problems Find v and i in the circuit V1 = 14 V 6 = V3 -
- 11. Mesh Analysis (Planar / Nonplanar) mesh analysis applies KVL to find mesh currents Mesh analysis is
- 12. Mesh Analysis A mesh (independent loop) is a loop which does not contain any other loops
- 13. Example For the circuit, find the branch currents using mesh analysis
- 14. Problem Use mesh analysis to find the current I0 in the circuit
- 15. Problem Use mesh analysis to find the current I0 in the circuit
- 17. Mesh Analysis with Current Sources the presence of the current sources reduces the number of equations
- 18. Example For the circuit, find i1 to i4 using mesh analysis i3 = i2 + 3*i4
- 19. Nodal and Mesh Analyses by Inspection (G1+G2)*v1 – G2*v2 = I1 – I2 (G2+G3)*v2 – G2*v1
- 20. Nodal Versus Mesh Analysis first factor is the nature of the particular network Networks that contain
- 22. Скачать презентацию


















 Сила тяжести
Сила тяжести Понятие классической – макроскопической теории электромагнитного поля
Понятие классической – макроскопической теории электромагнитного поля 540576.pptx
540576.pptx Изучение физических свойств кристаллов из NaCl и CuSO4
Изучение физических свойств кристаллов из NaCl и CuSO4 Строения атомов
Строения атомов Дифракционная решётка
Дифракционная решётка Випробування металів та сплавів на твердість за методом. Лабораторна робота №2
Випробування металів та сплавів на твердість за методом. Лабораторна робота №2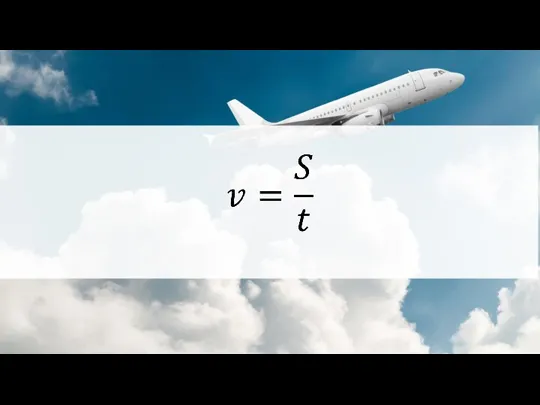 Расчёт пути и времени движения
Расчёт пути и времени движения Ускорение свободного падения а земле и других небесных телах
Ускорение свободного падения а земле и других небесных телах Червячные передачи
Червячные передачи Выбор шин по действию тока короткого замыкания
Выбор шин по действию тока короткого замыкания Расчет сопротивления проводника
Расчет сопротивления проводника Тепловые двигатели
Тепловые двигатели Физические основы механики
Физические основы механики Движение и взаимодействие тел. 7 класс
Движение и взаимодействие тел. 7 класс Измерение давления
Измерение давления Интегрированный урок по теме: Копченые продукты со вкусом физики и запахом истории
Интегрированный урок по теме: Копченые продукты со вкусом физики и запахом истории Спектры. Наблюдение сплошного и линейчатого спектров излучения ионизированных газов
Спектры. Наблюдение сплошного и линейчатого спектров излучения ионизированных газов Принцип Гюйгенса. Закон отражения света. Плоские и сферические зеркала. Закон преломления света. Полное внутреннее отражение
Принцип Гюйгенса. Закон отражения света. Плоские и сферические зеркала. Закон преломления света. Полное внутреннее отражение Качественные задачи
Качественные задачи Модельный ряд двигателей ЗМЗ
Модельный ряд двигателей ЗМЗ Колебательный контур. Подготовка к ЕГЭ
Колебательный контур. Подготовка к ЕГЭ Разработка систем аварийной посадки квадрокоптера
Разработка систем аварийной посадки квадрокоптера Решение задач
Решение задач Достижения современной физики в нашей жизни. Производные предлоги. Узкоспециальные термины. Глаголы с абстрактным значением
Достижения современной физики в нашей жизни. Производные предлоги. Узкоспециальные термины. Глаголы с абстрактным значением Тепловые явления
Тепловые явления Проект Jaguar
Проект Jaguar Исследование механических характеристик композитных материалов (КМ). Проектирование пакета слоёв
Исследование механических характеристик композитных материалов (КМ). Проектирование пакета слоёв