Содержание
- 2. Учебные цели: Кафедра №2, ВАС Научиться синтезировать БИХ-фильтры методом билинейного Z-преобразования с использованием пакета программ FD3.
- 3. Учебные вопросы: Кафедра №2, ВАС Пример синтеза фильтра по заданным требованиям. Расчёт добротностей полюсов. Конструирование каскадной
- 4. Первый учебный вопрос Кафедра №2, ВАС Пример синтеза фильтра по заданным требованиям
- 5. Кафедра №2, ВАС 16 Первый учебный вопрос 1. Задание требований: частота дискретизации fд = 2000 Гц;
- 6. Второй учебный вопрос Кафедра №2, ВАС Расчёт добротностей полюсов
- 7. Второй учебный вопрос Кафедра №2, ВАС Добротность Qk k-го нуля или полюса определяется по формуле: где
- 8. Второй учебный вопрос Кафедра №2, ВАС Добротность Qk k-го нуля или полюса определяется по формуле: где
- 9. Второй учебный вопрос Кафедра №2, ВАС Добротность Qk k-го нуля или полюса определяется по формуле: где
- 10. Третий учебный вопрос Кафедра №2, ВАС Конструирование каскадной (последовательной) схемы
- 11. Кафедра №2, ВАС 1. Формирование биквадратных звеньев и расположение их в каскадной структуре. Вследствие полученных результатов
- 12. Кафедра №2, ВАС 1. Формирование биквадратных звеньев и расположение их в каскадной структуре. Вследствие полученных результатов
- 13. Кафедра №2, ВАС 1. Формирование биквадратных звеньев и расположение их в каскадной структуре. Вследствие полученных результатов
- 14. Кафедра №2, ВАС 1. Формирование биквадратных звеньев и расположение их в каскадной структуре. Вследствие полученных результатов
- 15. Кафедра №2, ВАС 1. Формирование биквадратных звеньев и расположение их в каскадной структуре. Вследствие полученных результатов
- 16. Кафедра №2, ВАС 2. Оптимизация структуры звеньев с целью достижения минимума собственного шума, приведённого к выходу.
- 17. Кафедра №2, ВАС 3. Запись передаточной функции с учётом коэффициентов масштабирования. С целью уменьшения числа умножителей
- 18. Четвертый учебный вопрос Кафедра №2, ВАС Система разностных уравнений
- 20. Скачать презентацию

















 Презентация на тему Однофазный мостовой выпрямитель
Презентация на тему Однофазный мостовой выпрямитель  Фиксаторы движущихся деталей или узлов
Фиксаторы движущихся деталей или узлов ВКР: Методика определения глубины максимума ШАЛ по длительности импульса Черенковского излучения
ВКР: Методика определения глубины максимума ШАЛ по длительности импульса Черенковского излучения Явление электромагнитной индукции
Явление электромагнитной индукции Презентация на тему Телевидение
Презентация на тему Телевидение  Входной контроль
Входной контроль Влияние химической связи на свойства материалов
Влияние химической связи на свойства материалов Определение фокусного расстояния линзы. Лабораторная работа
Определение фокусного расстояния линзы. Лабораторная работа Исследование полей Токов смещения
Исследование полей Токов смещения Волшебница вода
Волшебница вода Законы Ньютона
Законы Ньютона Силы в механике. Решение задач. Урок физики в 10 классе
Силы в механике. Решение задач. Урок физики в 10 классе Необычные свойства обычной воды
Необычные свойства обычной воды Равновесие тел
Равновесие тел Основи термодинаміки
Основи термодинаміки Ток проводимости в металлах, его характеристики и условия существования
Ток проводимости в металлах, его характеристики и условия существования Области применения ультрафиолетового и инфракрасного излучений
Области применения ультрафиолетового и инфракрасного излучений Теория гироскопов
Теория гироскопов Звук. Колебательные системы
Звук. Колебательные системы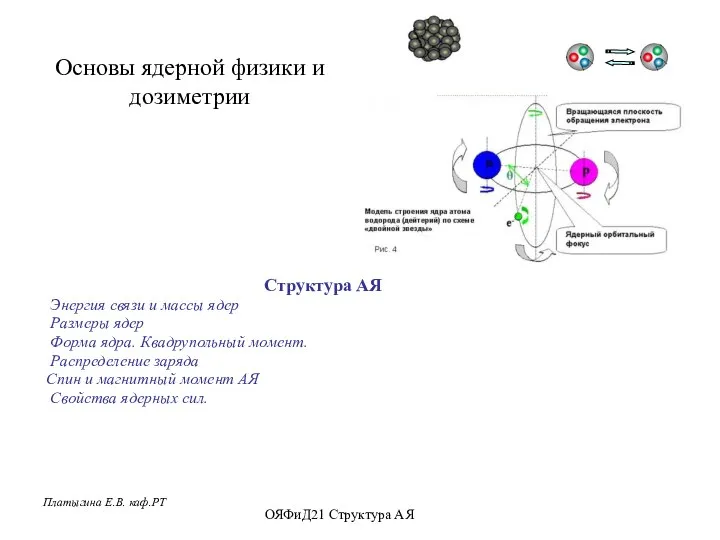 Основы ядерной физики и дозиметрии
Основы ядерной физики и дозиметрии Электрический ток. Соединения проводников
Электрический ток. Соединения проводников Разработка адаптивного метода оценки характеристик досмотровых комплексов с функцией распознавания материалов объектов контроля
Разработка адаптивного метода оценки характеристик досмотровых комплексов с функцией распознавания материалов объектов контроля Электрические цепи. Последовательное и параллельное соединение проводников
Электрические цепи. Последовательное и параллельное соединение проводников Презентация на тему Магнитное поле катушки с током. Электромагниты
Презентация на тему Магнитное поле катушки с током. Электромагниты  Электрическая цепь. Основные законы
Электрическая цепь. Основные законы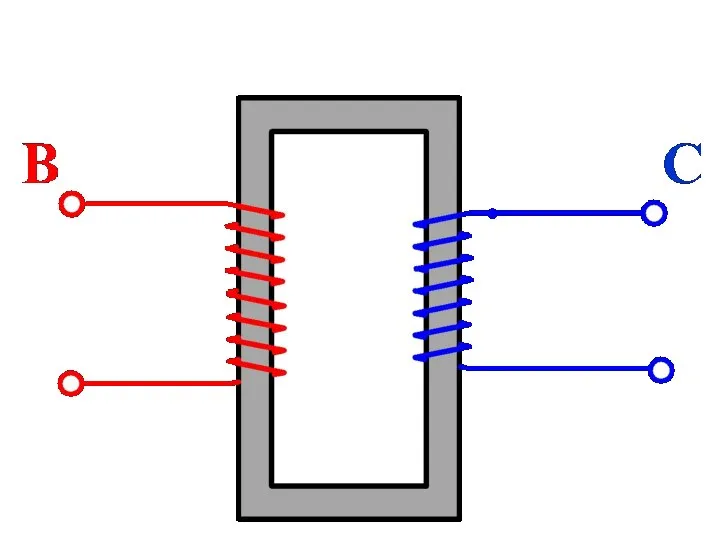 Автотрансформаторы
Автотрансформаторы Элементарные частицы. Античастицы
Элементарные частицы. Античастицы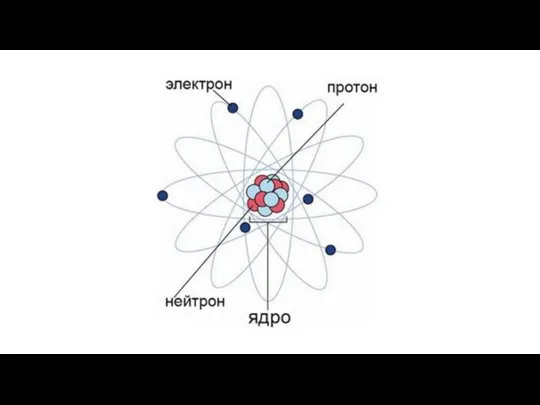 Строение атома
Строение атома