Содержание
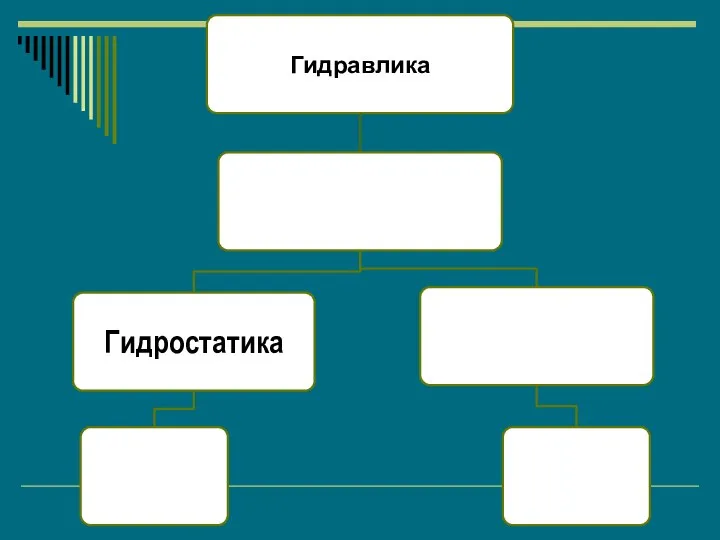
- 2. Основы гидравлики
- 4. - физические тела, которые легко изменяют свою форму под действием приложенных сил. Капельные Газообразные характеризуются малой
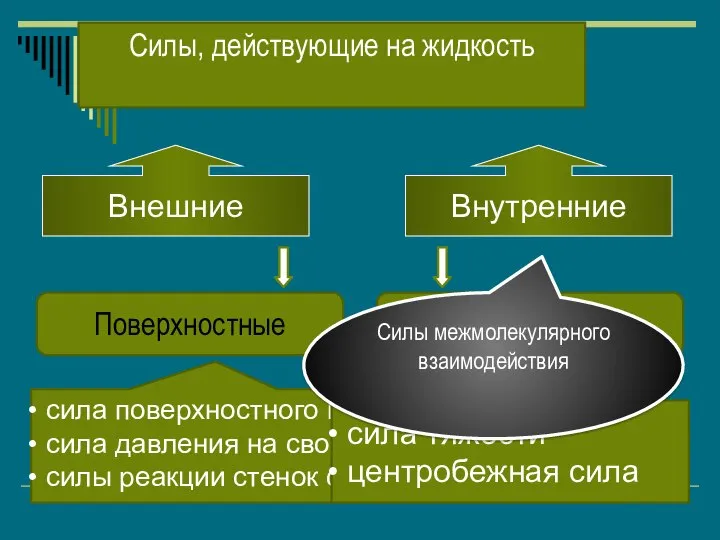
- 5. Внешние Внутренние Поверхностные Объемные сила поверхностного натяжения сила давления на свободную поверхность силы реакции стенок сосуда
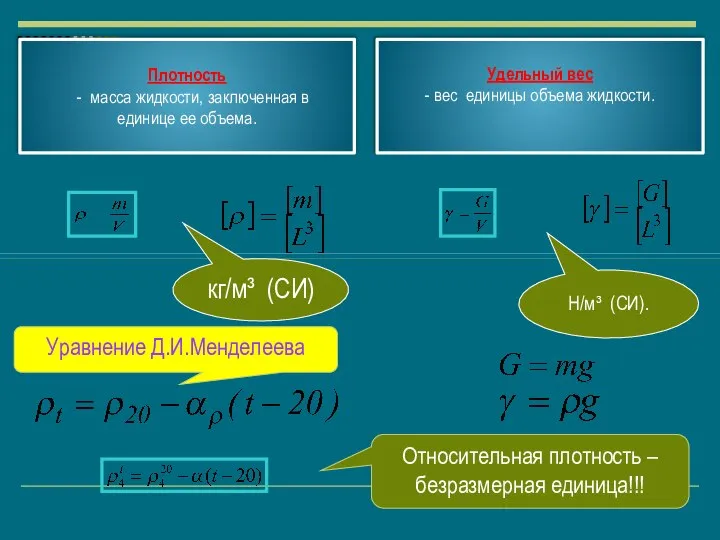
- 7. кг/м³ (СИ) Н/м³ (СИ). Плотность - масса жидкости, заключенная в единице ее объема. Удельный вес -
- 8. Сжимаемость жидкостей характеризуется коэффициентом сжимаемости который равен отношению изменения относительного объема жидкости к изменению давления: (м2/Н).
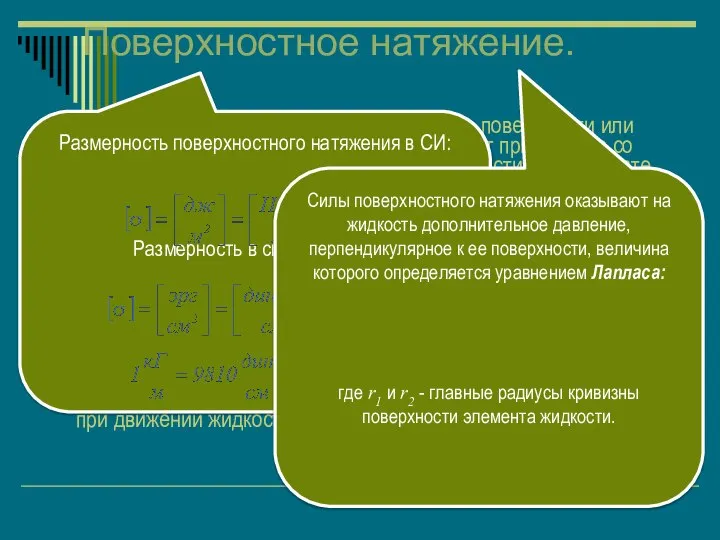
- 9. Поверхностное натяжение. Молекулы жидкости, расположенные на ее поверхности или непосредственно у поверхности, испытывают притяжение со стороны
- 10. Вязкость Вязкость является результатом действия трения между соприкасающимися слоями жидкости, вследствие чего эти слои движутся с
- 11. Вязкость Вязкостью называется свойство жидкости оказывать сопротивление ее движению, т.е. взаимному перемещению ее частиц. Напряжение внутреннего
- 12. Единицы измерения вязкости μ: Соотношение между Па*с и П: Кинематический коэффициент вязкости или кинематическая вязкость ν:
- 13. ГИДРОСТАТИКА
- 14. Не для конспекта Злобный джинн, находящийся в газообразном состоянии внутри закупоренной бутылки, оказывает сильное давление на
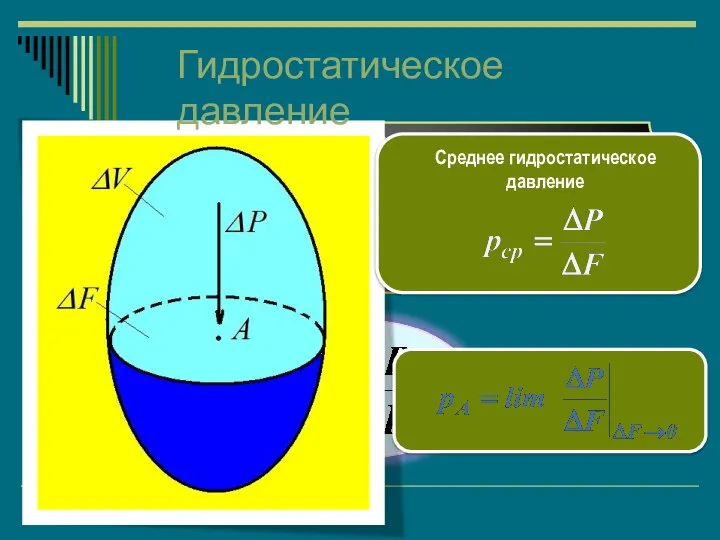
- 15. Давление жидкости на единицу поверхности называется гидростатическим давлением или просто давлением. Среднее гидростатическое давление Гидростатическое давление
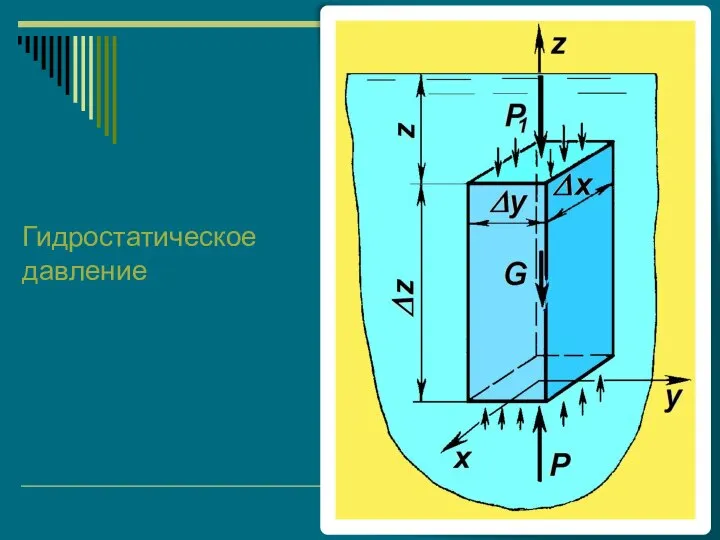
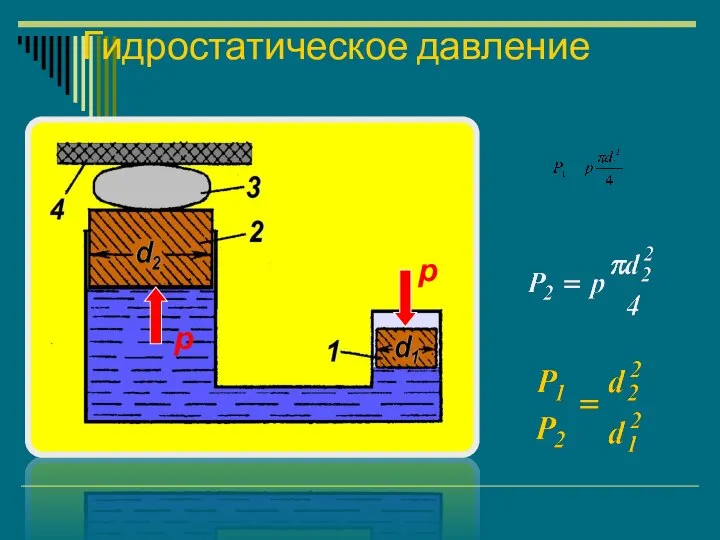
- 16. Гидростатическое давление
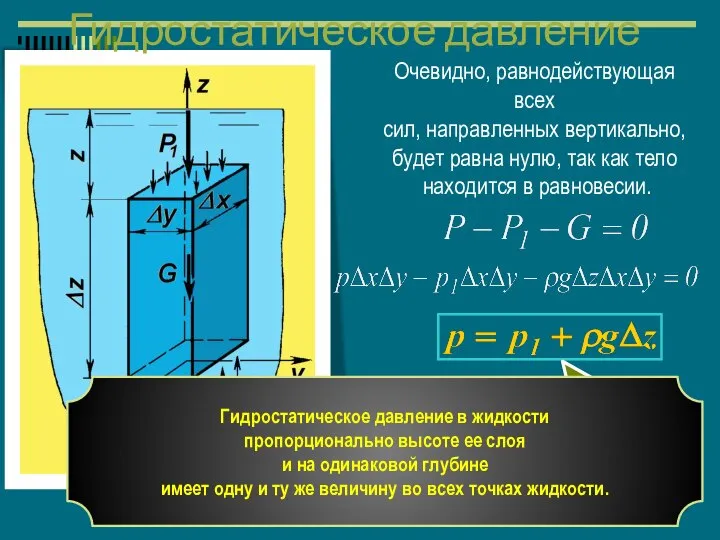
- 17. Очевидно, равнодействующая всех сил, направленных вертикально, будет равна нулю, так как тело находится в равновесии. основное
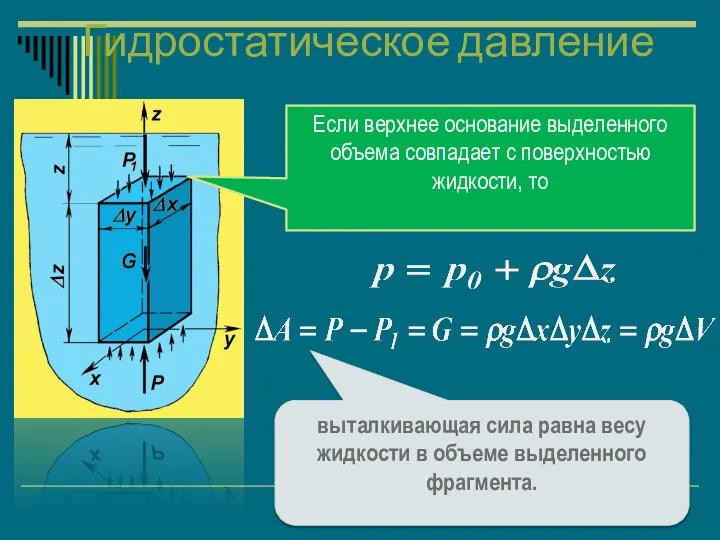
- 18. Гидростатическое давление выталкивающая сила равна весу жидкости в объеме выделенного фрагмента. Если верхнее основание выделенного объема
- 19. Гидростатическое давление Гидростатическое давление направлено по нормали к поверхности, на которую оно действует, а величина его
- 20. Гидростатическое давление р р
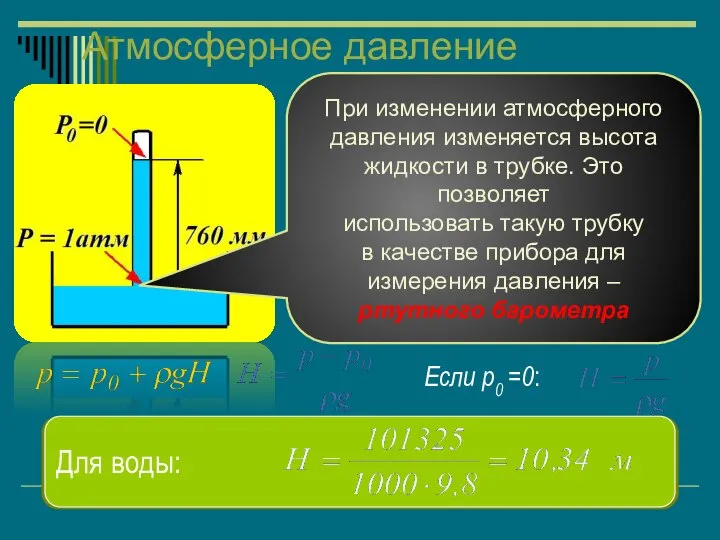
- 21. Атмосферное давление Атмосферное давление - это сила, действуюшая со стороны воздушной атмосферы на единицу площади поверхности
- 22. Атмосферное давление Если в жидкую ртуть опустить трубку, в которой создан вакуум, то ртуть под действием
- 23. Атмосферное давление Можно ли, пользуясь поршневым насосом, через шланг накачать воду из лужи во дворе в
- 24. Атмосферное давление Торичелли: не насос втягивает воду, а атмосферное давление её поднимает вверх, когда на всасывающей
- 25. Давление абсолютное, избыточное и разрежение (вакуум). Соотношения между единицами измерения давления: 1 атм (физ)= 760 мм
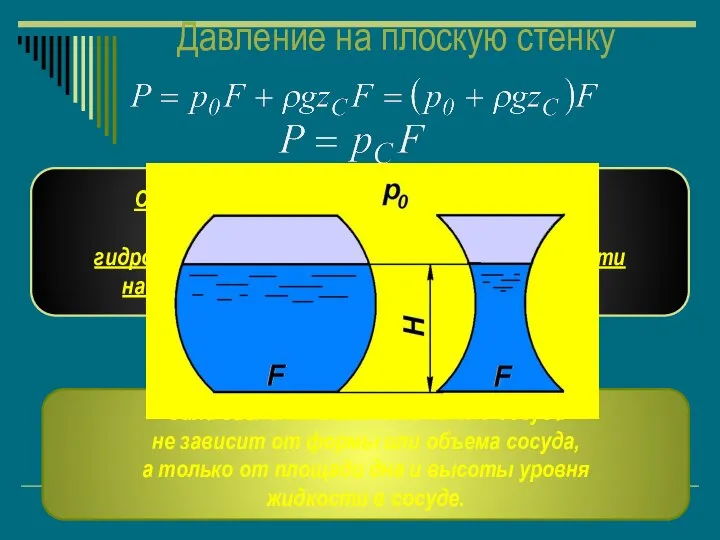
- 26. Давление на плоскую стенку Сила давления жидкости на плоскую стенку равна произведению величины гидростатического давления в
- 27. ГИДРОДИНАМИКА
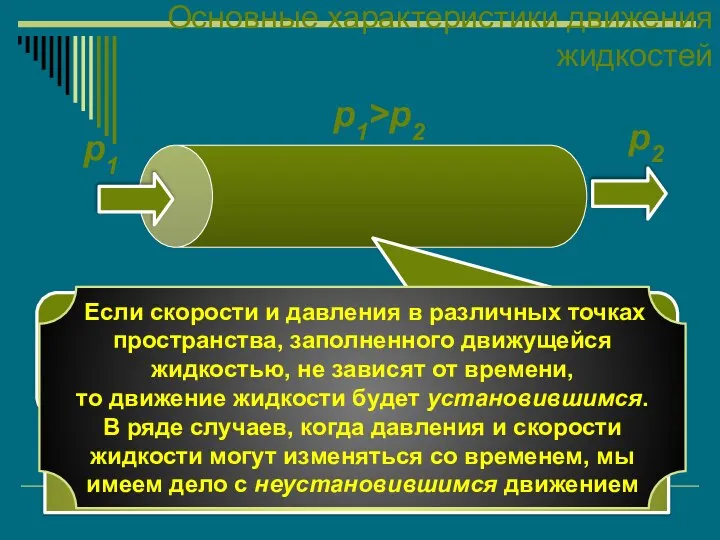
- 28. p1 p2 p1>p2 Движущей силой при течении жидкостей является разность давлений, которая создается с помощью насосов
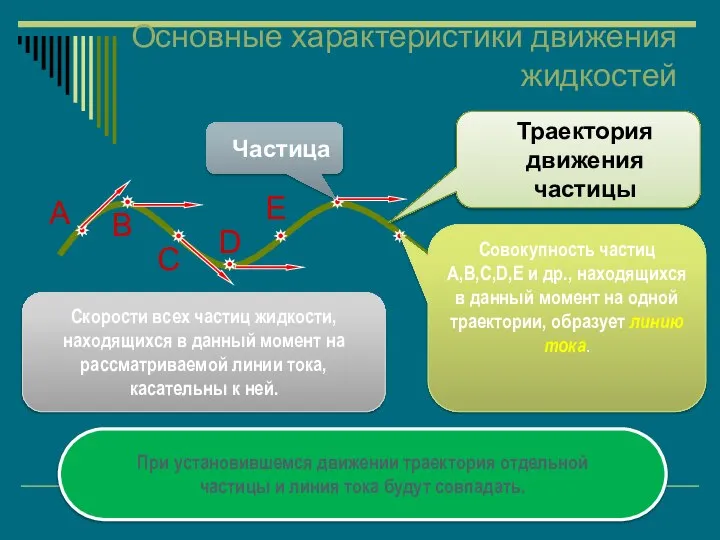
- 29. Основные характеристики движения жидкостей Траектория движения частицы Частица A B C D E Совокупность частиц A,B,C,D,E
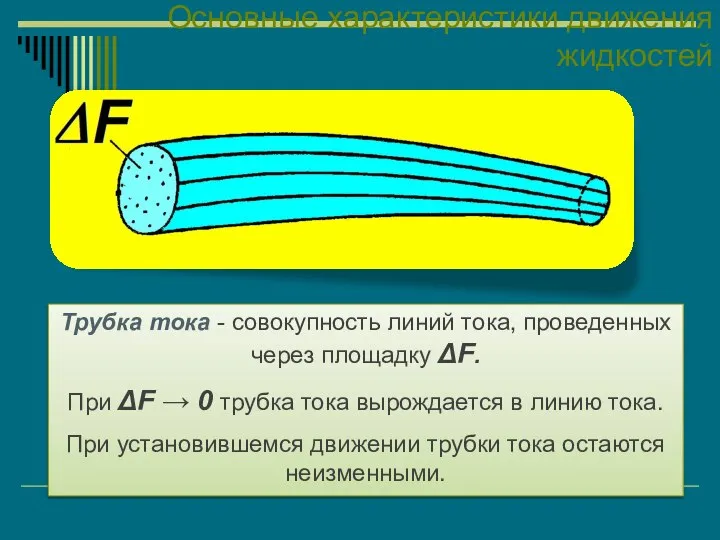
- 30. Основные характеристики движения жидкостей Трубка тока - совокупность линий тока, проведенных через площадку ΔF. При ΔF
- 31. Основные характеристики движения жидкостей Живое сечение потока - сечение потока, проведенное перпендикулярно к направлению линий тока.
- 32. Основные характеристики движения жидкостей Гидравлический (эквивалентный) радиус - отношение площади живого сечения потока F к смоченному
- 33. Скорость и расход жидкости Расход - количество жидкости, протекающее через живое сечение потока в единицу времени.
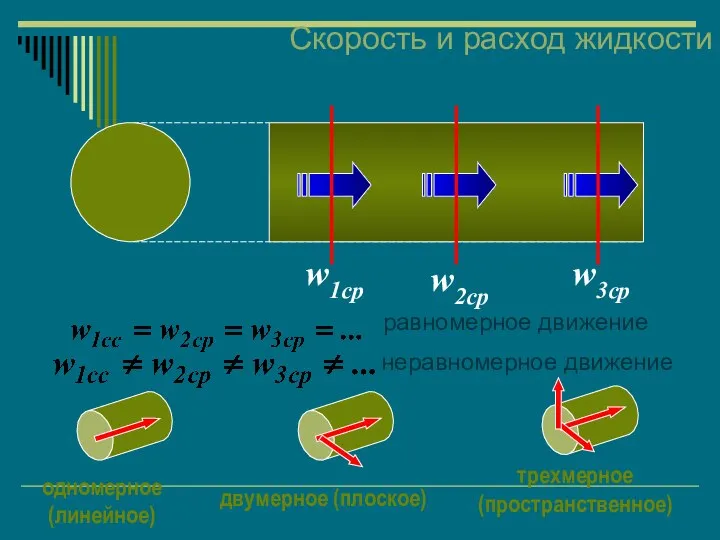
- 34. Скорость и расход жидкости w1ср w2ср w3ср равномерное движение неравномерное движение одномерное (линейное) двумерное (плоское) трехмерное
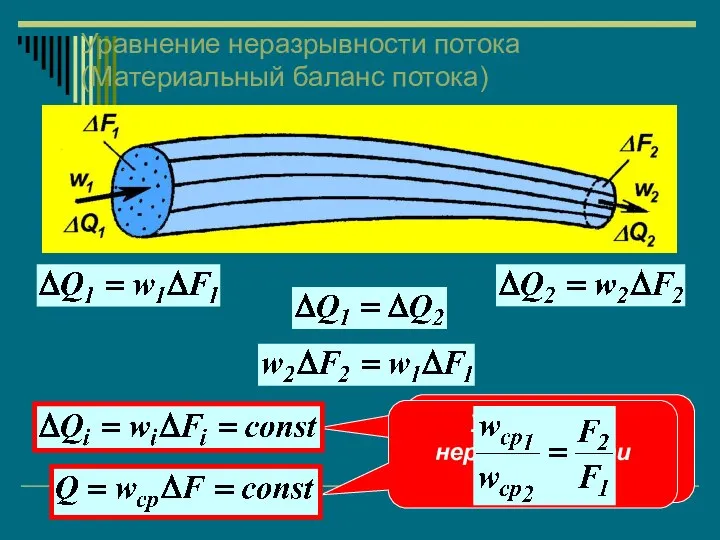
- 35. Уравнение неразрывности струи Уравнение неразрывности потока Уравнение неразрывности потока (Материальный баланс потока)
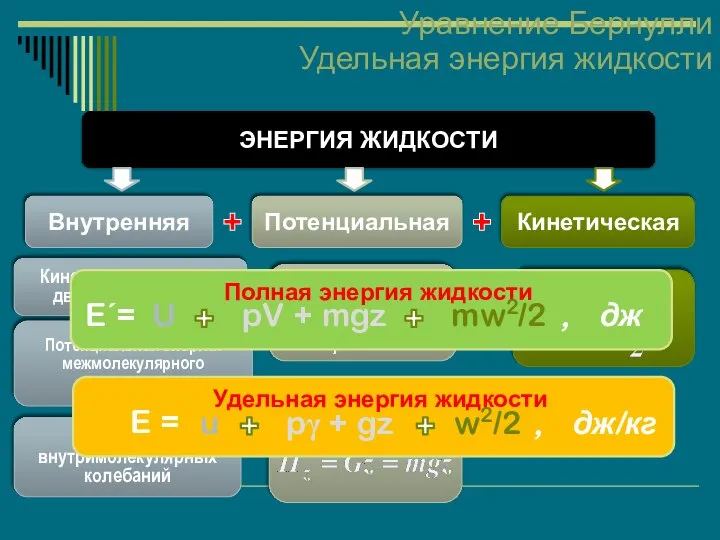
- 36. Уравнение Бернулли Удельная энергия жидкости ЭНЕРГИЯ ЖИДКОСТИ Внутренняя Потенциальная Кинетическая Кинетическая энергия движения молекул Потенциальная энергия
- 37. u1=u2 Уравнение Бернулли для идеальной жидкости уравнение Бернулли для идеальной жидкости. Уравнение Бернулли является частным случаем
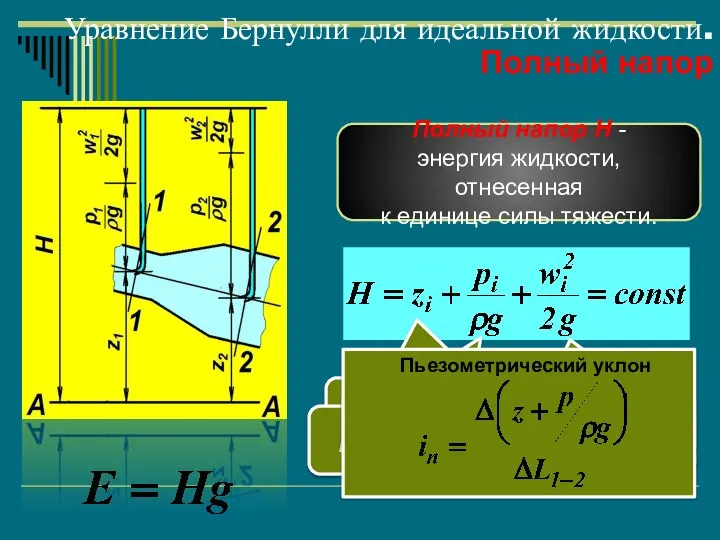
- 38. Уравнение Бернулли для идеальной жидкости. Полный напор Полный напор Н - энергия жидкости, отнесенная к единице
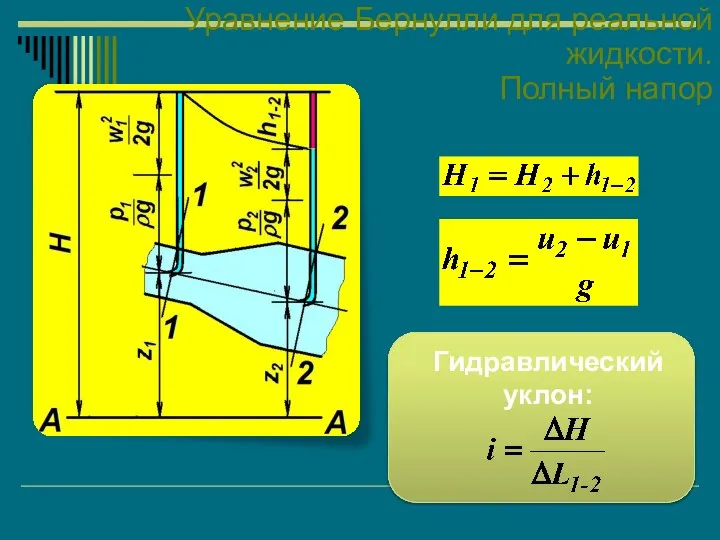
- 39. Уравнение Бернулли для реальной жидкости уравнение Бернулли для реальной жидкости. В отличие от идеальной жидкости, для
- 40. Уравнение Бернулли для реальной жидкости. Полный напор Гидравлический уклон:
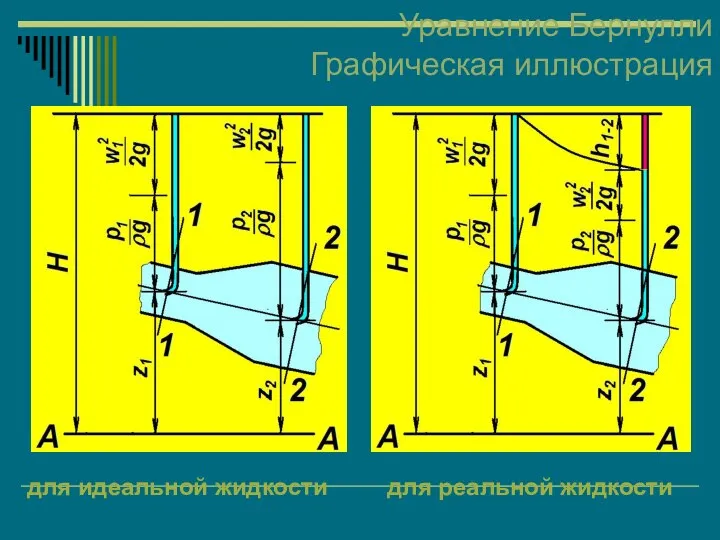
- 41. Уравнение Бернулли Графическая иллюстрация для идеальной жидкости для реальной жидкости
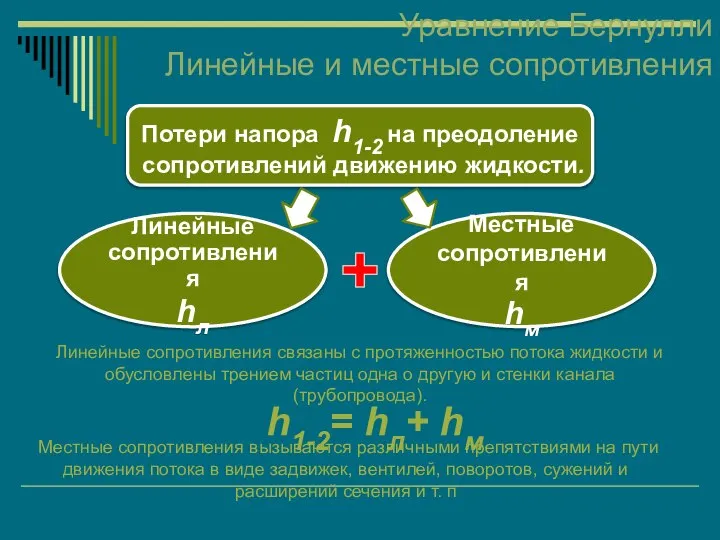
- 42. Уравнение Бернулли Линейные и местные сопротивления Потери напора h1-2 на преодоление сопротивлений движению жидкости. Линейные сопротивления
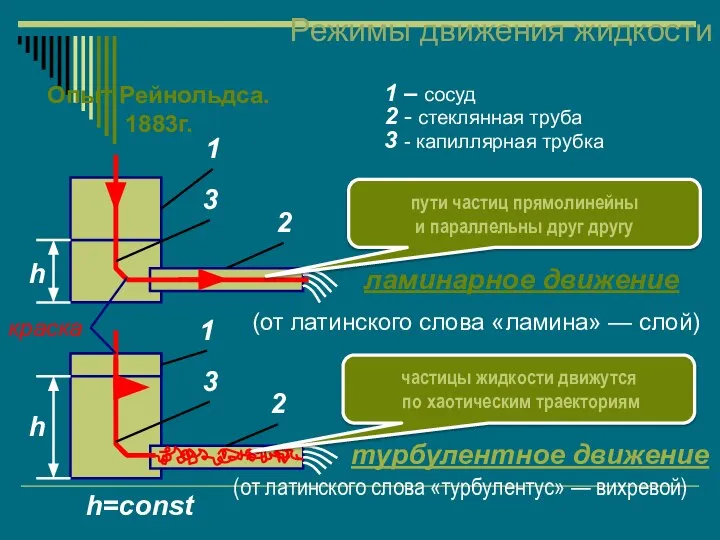
- 43. Режимы движения жидкости Опыт Рейнольдса. 1883г. краска h h h=const 2 2 1 – сосуд 2
- 44. Режимы движения жидкости Опыт показывает, что переход от ламинарного течения к турбулентному зависит от массовой скорости
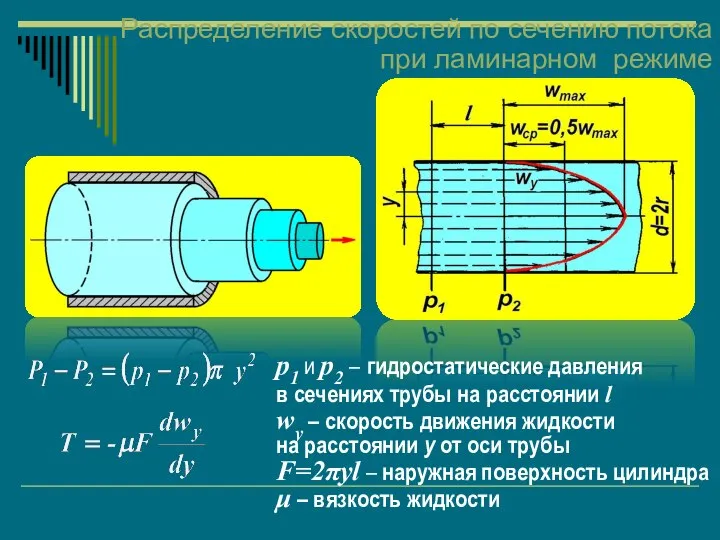
- 45. Распределение скоростей по сечению потока при ламинарном режиме р1 и р2 – гидростатические давления в сечениях
- 46. Распределение скоростей по сечению потока при ламинарном режиме Сумма проекций всех сил на ось потока равна
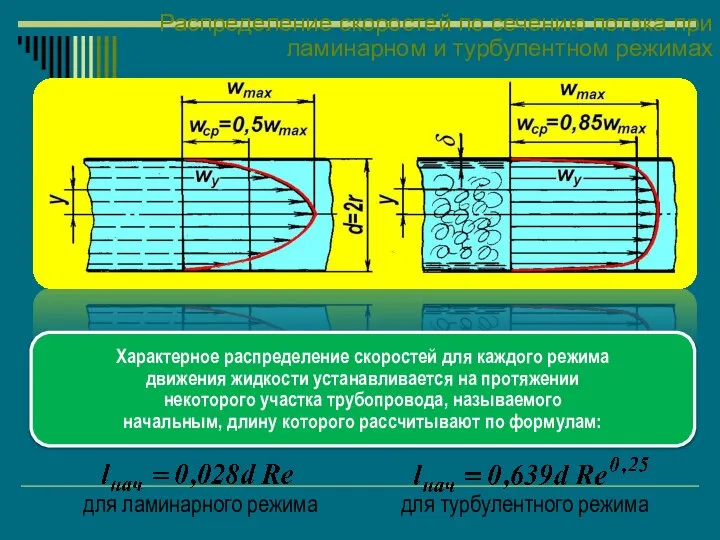
- 47. Распределение скоростей по сечению потока при ламинарном режиме При ламинарном потоке средняя скорость жидкости равна половине
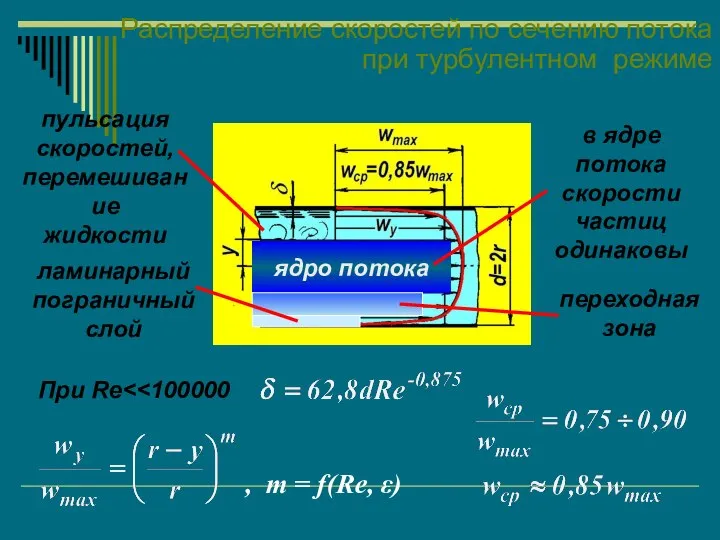
- 48. Распределение скоростей по сечению потока при турбулентном режиме пульсация скоростей, перемешивание жидкости ядро потока в ядре
- 49. Распределение скоростей по сечению потока при ламинарном и турбулентном режимах Характерное распределение скоростей для каждого режима
- 50. Некоторые практические приложения уравнения Бернулли
- 51. Сопротивление при движении жидкости по трубопроводу При движении реальной жидкости по трубопроводу или каналу происходит потеря
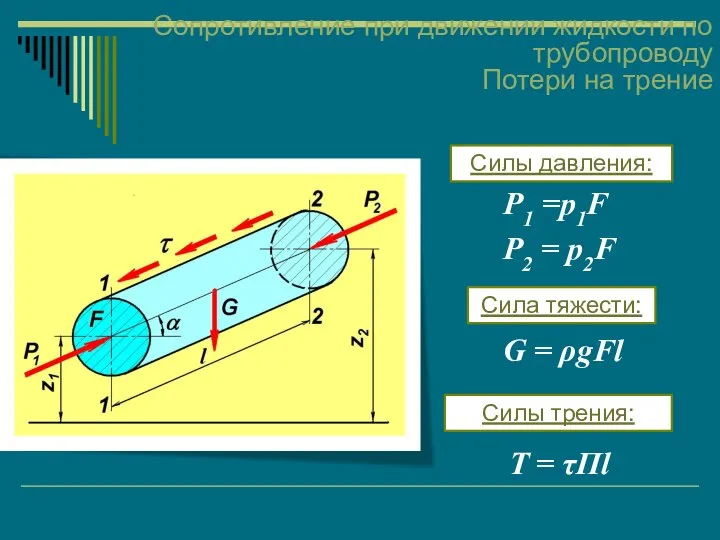
- 52. Сопротивление при движении жидкости по трубопроводу Потери на трение Р1 =p1F P2 = p2F G =
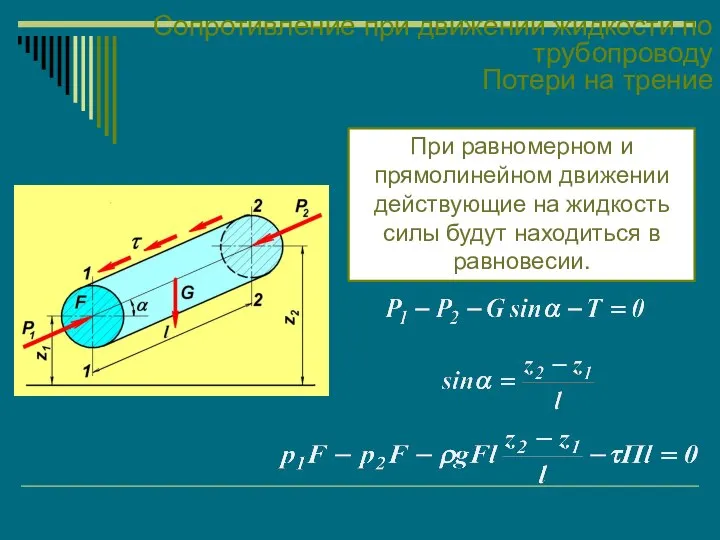
- 53. Сопротивление при движении жидкости по трубопроводу Потери на трение При равномерном и прямолинейном движении действующие на
- 54. Сопротивление при движении жидкости по трубопроводу Потери на трение Потери напора при равномерном движении: Разделим уравнение
- 55. Сопротивление при движении жидкости по трубопроводу Потери на трение Напряжение трения τ: Введем обозначение: — коэффициент
- 56. Сопротивление при движении жидкости по трубопроводу Потери на трение Потери напора на трение: Для круглого трубопровода
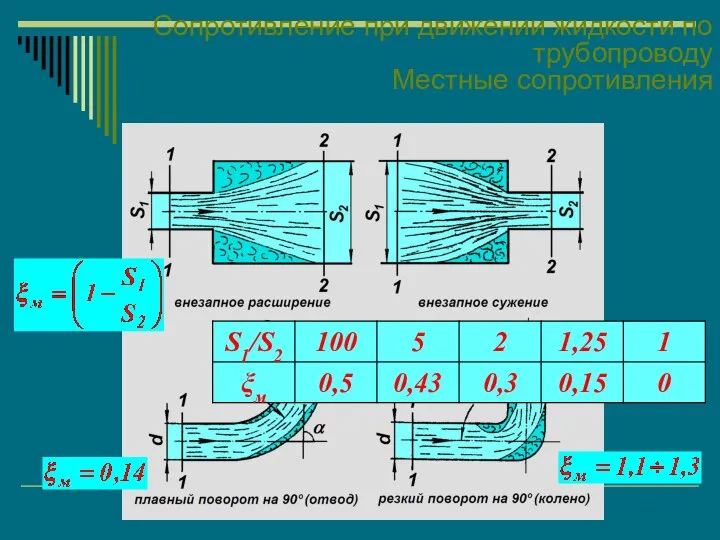
- 57. Сопротивление при движении жидкости по трубопроводу Местные сопротивления К местным сопротивлениям относятся вход в трубу и
- 58. Сопротивление при движении жидкости по трубопроводу Местные сопротивления
- 59. Сопротивление при движении жидкости по трубопроводу Общая потеря напора Полную потерю напора определяют как сумму всех
- 61. Скачать презентацию






























 Деформація
Деформація Вес воздуха. Атмосферное давление
Вес воздуха. Атмосферное давление Газовые законы
Газовые законы Презентация на тему Инфразвук
Презентация на тему Инфразвук  Методы и приборы для измерения влажности газовых сред
Методы и приборы для измерения влажности газовых сред Фотометрия. Дисперсия света
Фотометрия. Дисперсия света Взаимодействие нейтронов с веществом. Лекция № 06
Взаимодействие нейтронов с веществом. Лекция № 06 Тонкослойная хроматография
Тонкослойная хроматография Основы математического моделирования транспортных процессов и логистика
Основы математического моделирования транспортных процессов и логистика Проблемы применения нанотехнологии
Проблемы применения нанотехнологии Оптика. Основные законы оптики
Оптика. Основные законы оптики Плазменное состояние вещества
Плазменное состояние вещества Равномерное и равнопеременное движение
Равномерное и равнопеременное движение Дискретные случайные процессы (тема 7)
Дискретные случайные процессы (тема 7) Трудности теории Бора. Квантовая физика
Трудности теории Бора. Квантовая физика Сила тяжіння. Вага тіла. Невагомість
Сила тяжіння. Вага тіла. Невагомість Виды теплопередачи
Виды теплопередачи Презентация на тему Взаимодействие токов. Магнитное поле. Вектор магнитной индукции. Линии магнитной индукции
Презентация на тему Взаимодействие токов. Магнитное поле. Вектор магнитной индукции. Линии магнитной индукции  Применение первого начала термодинамики к изопроцессам
Применение первого начала термодинамики к изопроцессам Устройство для наматывания нижней нити на шпульку
Устройство для наматывания нижней нити на шпульку Ядерные реакции с тяжелыми ядрами. (Тема 2.2)
Ядерные реакции с тяжелыми ядрами. (Тема 2.2) Второй закон термодинамики
Второй закон термодинамики Электромагнитная индукция
Электромагнитная индукция Электромагнитные волны. Волновое уравнение электромагнитной волны
Электромагнитные волны. Волновое уравнение электромагнитной волны 11_ ОТС_ Модуляция и демодуляция 14
11_ ОТС_ Модуляция и демодуляция 14 Презентация на тему Основные положения молекулярно-кинетической теории
Презентация на тему Основные положения молекулярно-кинетической теории  Идеальный газ. Абсолютная температура. Макро и микропараметры
Идеальный газ. Абсолютная температура. Макро и микропараметры