Содержание
- 2. Кинематика. Основные понятия и величины. Предмет кинематики: Описание движения и связи между величинами, характеризующими это движение
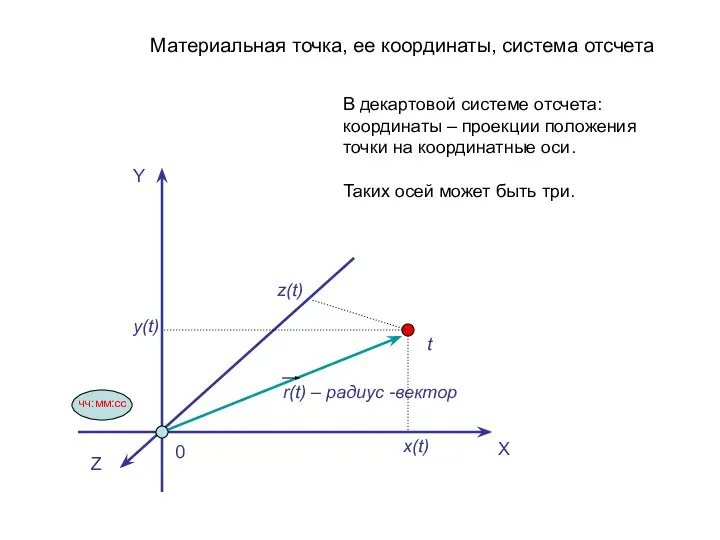
- 3. Материальная точка, ее координаты, система отсчета Y X Z z(t) y(t) x(t) 0 чч:мм:сс t r(t)
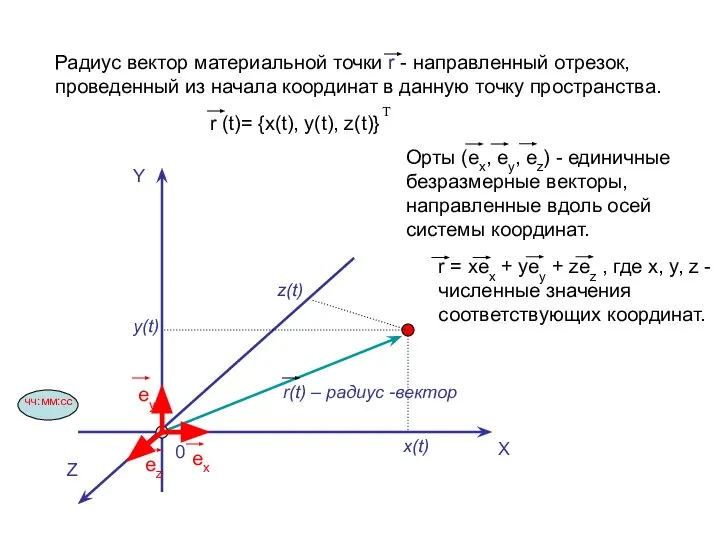
- 4. Y X Z z(t) y(t) x(t) 0 чч:мм:сс r(t) – радиус -вектор Радиус вектор материальной точки
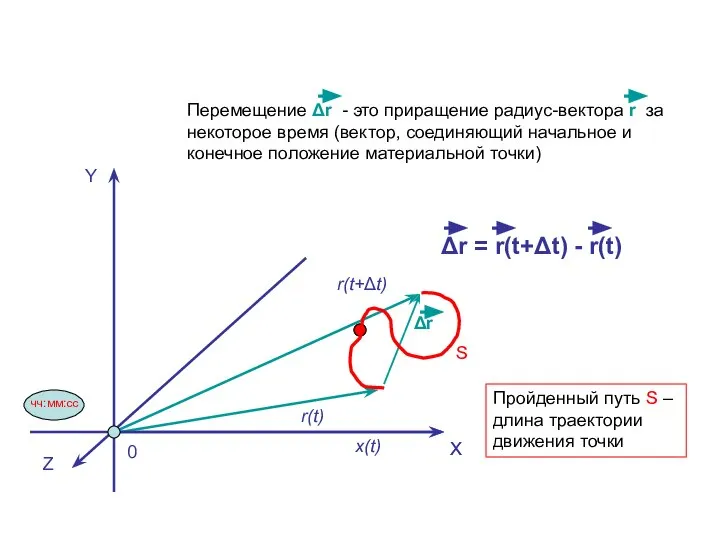
- 5. Перемещение, пройденный путь S X x(t) Δr S Перемещение Δr - это приращение радиус-вектора r за
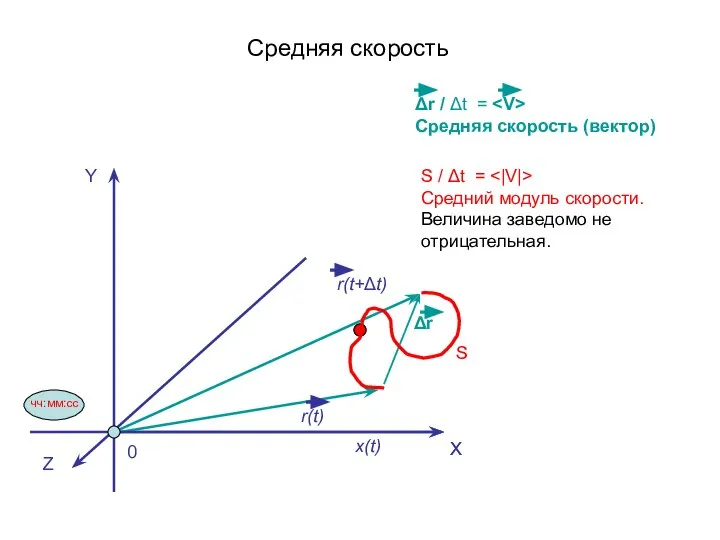
- 6. Средняя скорость Δr / Δt = Средняя скорость (вектор) S / Δt = Средний модуль скорости.
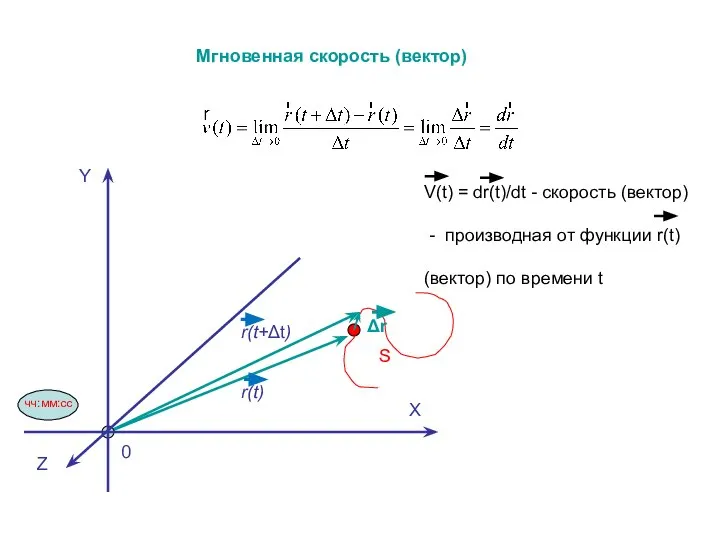
- 7. Y X Δr S r(t) Мгновенная скорость (вектор) r(t+Δt) Z 0 чч:мм:сс V(t) = dr(t)/dt -
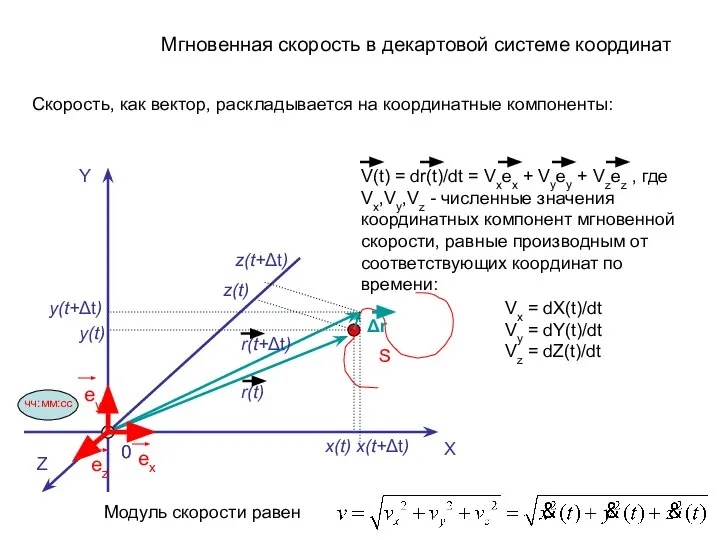
- 8. Y X z(t) y(t) x(t) x(t+Δt) Δr S r(t) r(t+Δt) Z 0 чч:мм:сс Vx = dX(t)/dt
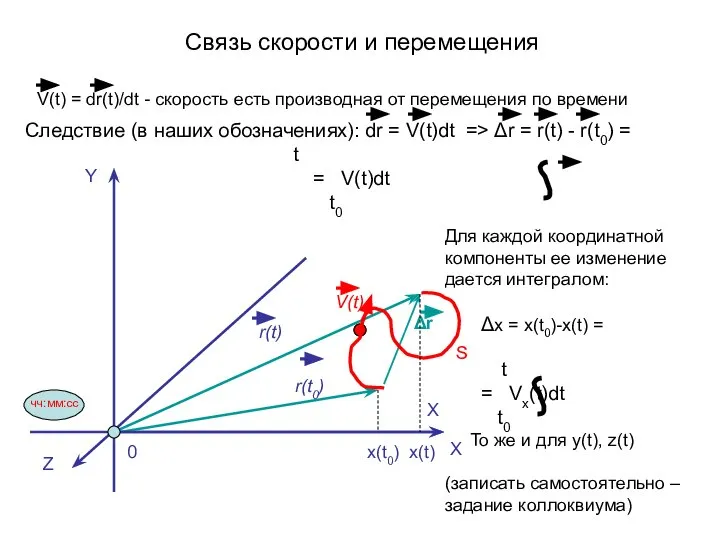
- 9. X Δr S Y X Z 0 чч:мм:сс r(t0) r(t) V(t) Следствие (в наших обозначениях): dr
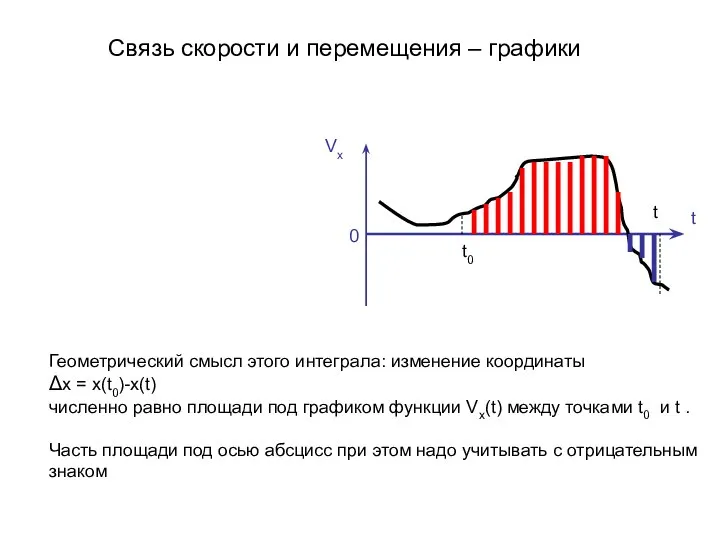
- 10. Vх t 0 Геометрический смысл этого интеграла: изменение координаты Δx = x(t0)-x(t) численно равно площади под
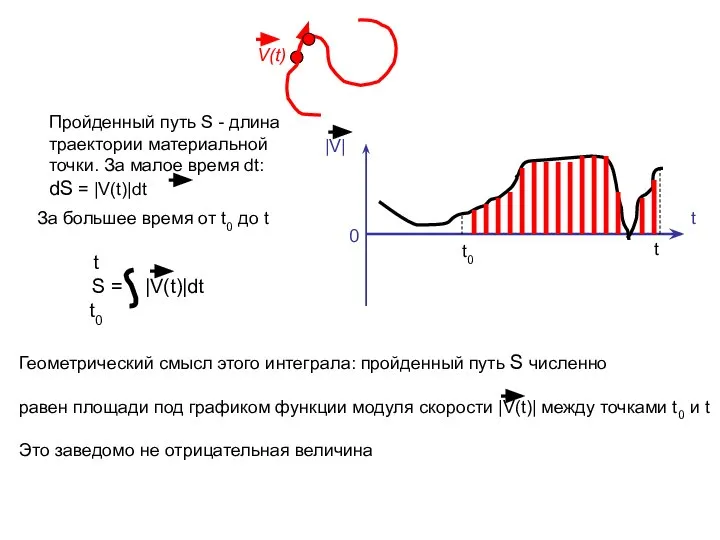
- 11. t 0 За большее время от t0 до t t S = |V(t)|dt t0 Геометрический смысл
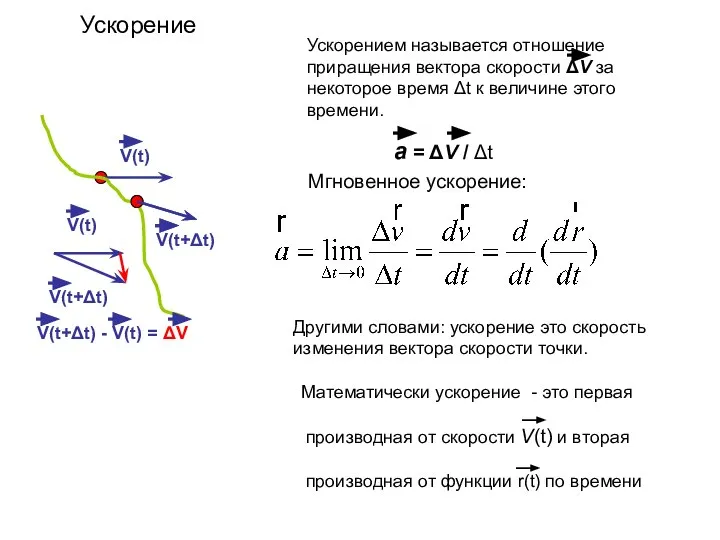
- 12. V(t) V(t+Δt) V(t) V(t+Δt) V(t+Δt) - V(t) = ΔV Другими словами: ускорение это скорость изменения вектора
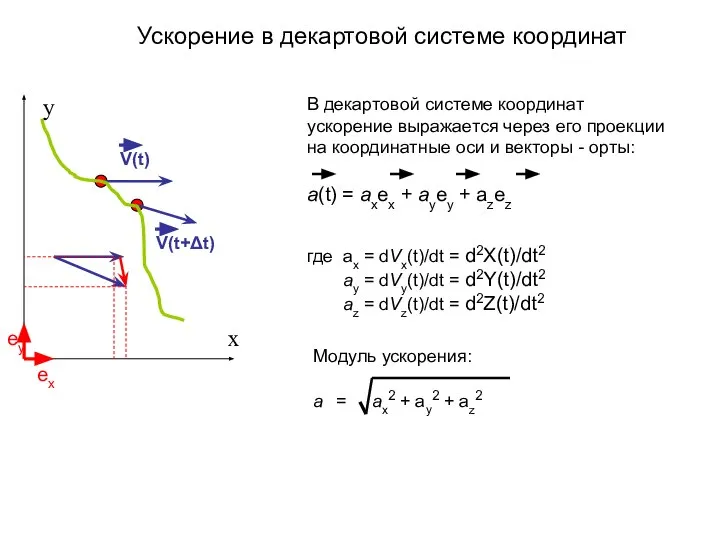
- 13. V(t) V(t+Δt) x y В декартовой системе координат ускорение выражается через его проекции на координатные оси
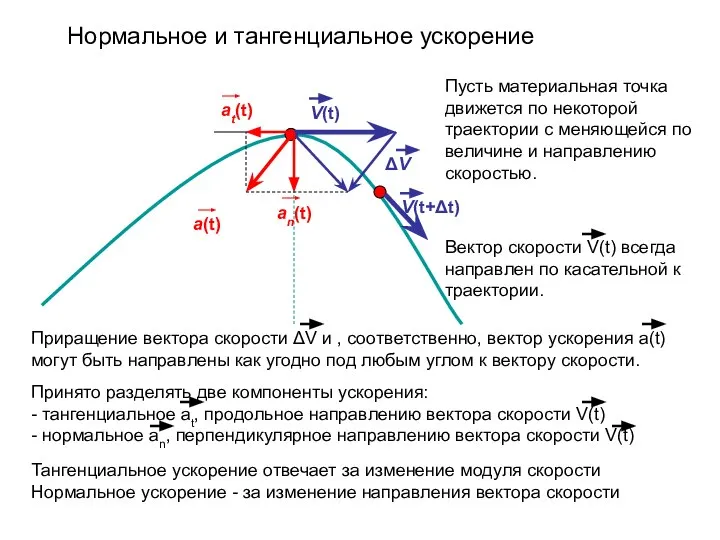
- 14. V(t) V(t+Δt) а(t) аt(t) аn(t) ΔV Пусть материальная точка движется по некоторой траектории с меняющейся по
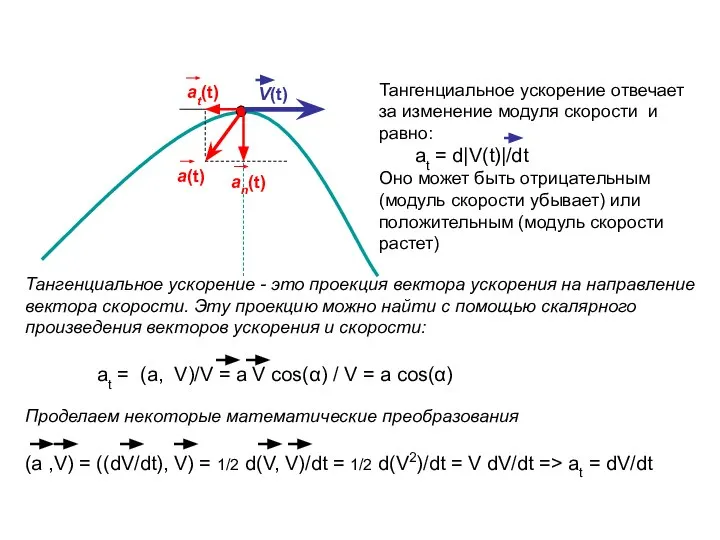
- 15. Тангенциальное ускорение отвечает за изменение модуля скорости и равно: аt = d|V(t)|/dt Оно может быть отрицательным
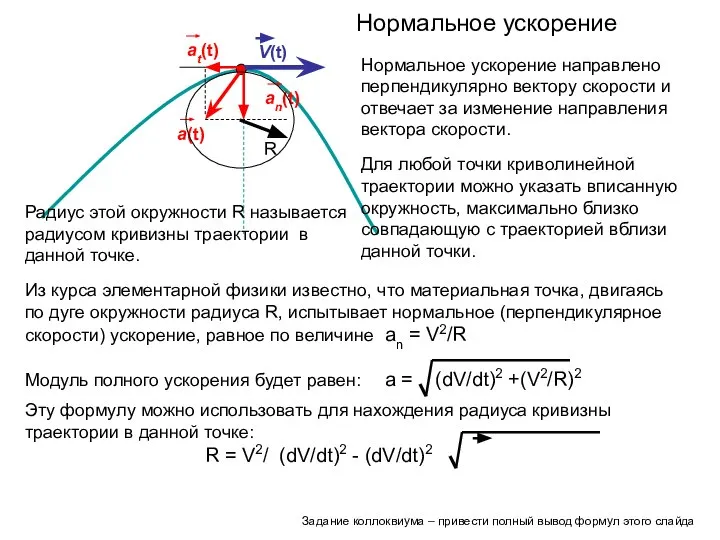
- 16. V(t) а(t) аt(t) аn(t) Нормальное ускорение направлено перпендикулярно вектору скорости и отвечает за изменение направления вектора
- 17. Абсолютно твердое тело: протяженный объект (система материальных точек) расстояния между которыми не изменяются в процессе движения
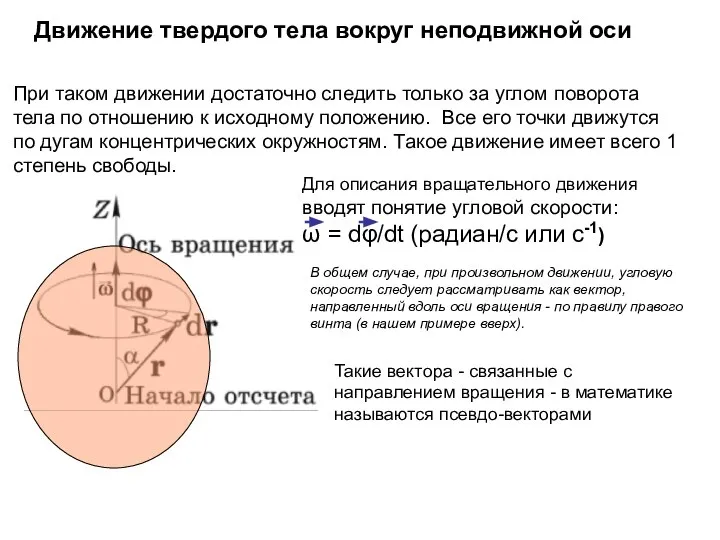
- 18. При таком движении достаточно следить только за углом поворота тела по отношению к исходному положению. Все
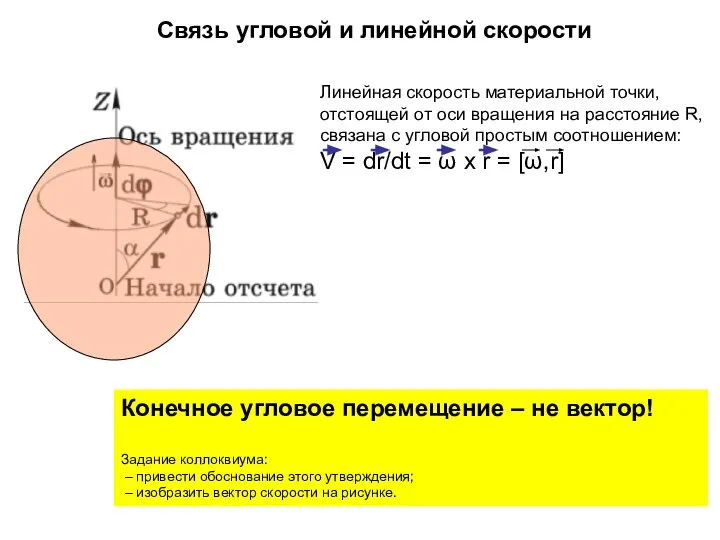
- 19. Связь угловой и линейной скорости Линейная скорость материальной точки, отстоящей от оси вращения на расстояние R,
- 20. Для описания неравномерного вращательного движения вводят понятие углового ускорения: β = dω/dt (радиан/с2 или с-2 )
- 22. Скачать презентацию



 Игра-соревнование Орешек знаний тверд
Игра-соревнование Орешек знаний тверд Естествознание
Естествознание Стандарт для определения состояния шарнира стойки стабилизатора
Стандарт для определения состояния шарнира стойки стабилизатора Горение свечи. Лабораторная работа
Горение свечи. Лабораторная работа Антифрикционные материалы
Антифрикционные материалы Вещества и явления в окружающем мире
Вещества и явления в окружающем мире Обнаружение магнитного поля по его действию на электрический ток
Обнаружение магнитного поля по его действию на электрический ток Проект В царстве Архимеда
Проект В царстве Архимеда Явление электромагнитной индукции
Явление электромагнитной индукции Международная система единиц. Единство измерений. Лекция № 2
Международная система единиц. Единство измерений. Лекция № 2 Виды энергии
Виды энергии Электрондық гармоникалық сигнал генераторлары Шаршы толқын генераторлары
Электрондық гармоникалық сигнал генераторлары Шаршы толқын генераторлары Семинар. Электричество
Семинар. Электричество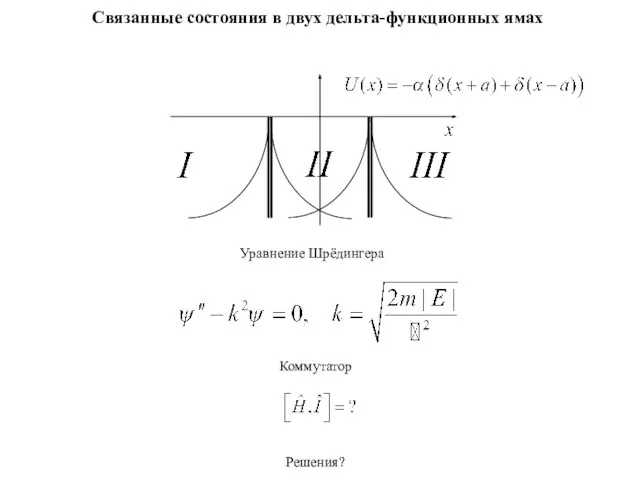 Связанные состояния в двух дельта - функционных ямах
Связанные состояния в двух дельта - функционных ямах Геотермальная энергия
Геотермальная энергия Основные понятия кинематики. Кинематика точки. Тема 1.7. Лекция 9
Основные понятия кинематики. Кинематика точки. Тема 1.7. Лекция 9 Тема 7. Действия в условиях негативных и опасных факторов бытового характера
Тема 7. Действия в условиях негативных и опасных факторов бытового характера Тема 1. Материя. Проект: Путёвка в жизнь
Тема 1. Материя. Проект: Путёвка в жизнь Закон Архимеда
Закон Архимеда Строение газообразных, жидких и твёрдых тел. 5 класс
Строение газообразных, жидких и твёрдых тел. 5 класс Физический КВН
Физический КВН Презентация на тему Создания вечного двигателя
Презентация на тему Создания вечного двигателя  Физический турнир
Физический турнир Форма и характеристики электрических сигналов. Анализ
Форма и характеристики электрических сигналов. Анализ Параметры светильников
Параметры светильников Швейная машина. 5 класс
Швейная машина. 5 класс Взаимодействие заряженных тел. Решение задач: закон Кулона
Взаимодействие заряженных тел. Решение задач: закон Кулона 9 класс
9 класс